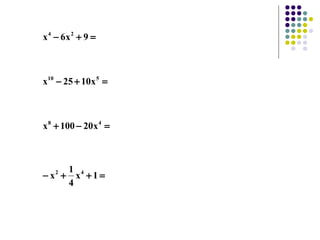Este documento trata sobre la factorización de polinomios. Explica diferentes métodos para factorizar polinomios incluyendo factor común, trinomio cuadrado perfecto, diferencia de cuadrados, y casos combinados. Proporciona ejemplos para ilustrar cada método.

1. FACTORIZACION DE
POLINOMIOS
TRANSFORMACION EN
PRODUCTO

2. CASOS:
 FACTOR COMUN
 FACTOR COMUN POR GRUPOS
 TRINOMIO CUADRADO PERFECTO
 CUATRINOMIO CUBO PERFECTO
 DIFERENCIA DE CUADRADOS
 SUMA O DIFERENCIA DE POTENCIAS DE IGUAL
EXPONENTE
 TEOREMA DE GAUSS
 ECUACIONES CUADRÁTICAS

3. FACTOR COMUN
 3X+6 = 3 . (X+2)
(
6x 5 + 18x 3 + 9x 2 = 3x 2 ⋅ 2x 3 + 6x + 3 )
Maximo común divisor de los x con el menor Cada termino se divide por el
coeficientes del polinomio exponente factor común

4. Ejemplos
1) 2 x 4 − 3 x 3 = 2) 10 x 4 − 2 x 3 + 4 x 2 =
1 1
3) x 2 + 2 x − x 3 = 4) x 3 + x =
2 8
5) x 7 + 5 x 5 − 3x 4 = 6) 3x 6 + 18 =
7) 10 x 5 + 15 x 4 − 5 x 3 + 10 x 2 = 8) 6 x 2 + 5 x − 1 =
10 5 10
9) x 4 − x 3 + x 6 = 10) 4 x 8 − 2 x 3 + 8 x 5 =
3 6 9
11) 7 x 5 + 5 x 4 + x 3 = 12) 2 x 4 − 6 x 3 + 4 x 2 =
1 1 1 1
13) − 4 x 7 − 8 x 3 + 4 x 2 + 16 x = 14) a 2 − a + a 3 − a 7 =
2 6 4 8

5. FACTOR COMUN POR
GRUPOS
2 5 4 3 1 2 2
x + x − x − =
3 3 3 3
primero extraemos factor comun :
1
3
(
⋅ 2x 5 + 4x 3 − x 2 − 2 )
agrupamos :
( 2x 5
) ( )
+ 4x 3 + − x 2 − 2 =
2x ⋅ ( x + 2 ) − 1( x + 2 ) =
3 2 2
( 2 x − 1) ⋅ ( x + 2 )
3 2
⋅ ( 2 x − 1) ⋅ ( x + 2 )
1 3 2
3

6. Ejemplos:
3x 7 − x 5 + 24x 2 − 8 =
2a − 2a − 3a + 3 =
5 3 2

7. Trinomio Cuadrado Perfecto
( a + b ) 2 = a 2 + 2ab + b 2 •Deben ser 3 términos
•2 de esos términos deben ser positivos
x 2 + 2 x + 1 = ( x + 1)
2
y tener raíz cuadrada
•El otro termino debe ser el doble
producto de las bases obtenidas
x 2.x.1 1 •El resultado será el cuadrado de la
suma o diferencia de las bases
•El signo lo determina el termino del
doble producto

8. x 4 − 6x 2 + 9 =
x10 − 25 + 10x 5 =
x 8 + 100 − 20x 4 =
1 4
− x + x +1=
2
4

9. Para practicar:
casos combinados
1)6x 5 − 12x 4 + 3x 3 =
2)2x 5 − 8x 4 + 4x 2 − 16x =
6 5 9 4 12 3 18 2
3) x − x − x + x =
5 5 5 5
4 )3 x 6 − 6 x 4 + 3x 2 =
5 )2 x 7 − 4 x 4 + 8 x =

10. Respuestas:
(
1)3x 3 ⋅ 2x 2 − 4x + 1 )
2 )2 x ⋅ ( x − 4 ) ⋅ x 3 + 2 ( )
3 2
3) x ⋅ ( 2x − 3 ) ⋅ x 2 − 2
5
( )
(
4 )3 x x − 1
2 2
) 2
(
5 )2 x x − 2 3
) 2