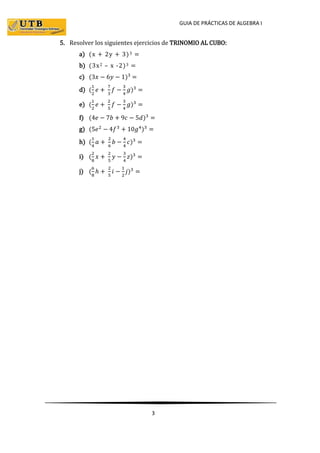Incrustar presentación
Descargado 181 veces


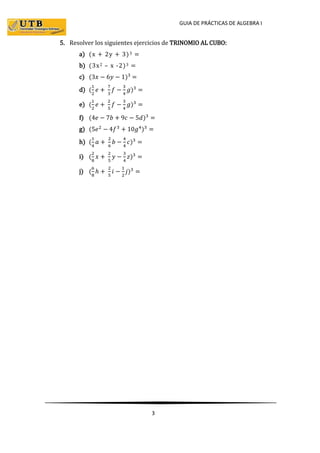
Este documento presenta una guía de prácticas de álgebra que incluye ejercicios sobre productos notables como el binomio al cuadrado, la diferencia de cuadrados, el trinomio al cuadrado, el binomio al cubo y el trinomio al cubo. Contiene más de 100 ejercicios para resolver que involucran expresiones algebraicas con variables como x, y, a, b y c entre otras. El objetivo es practicar diferentes tipos de productos notables que son fundamentales en álgebra.