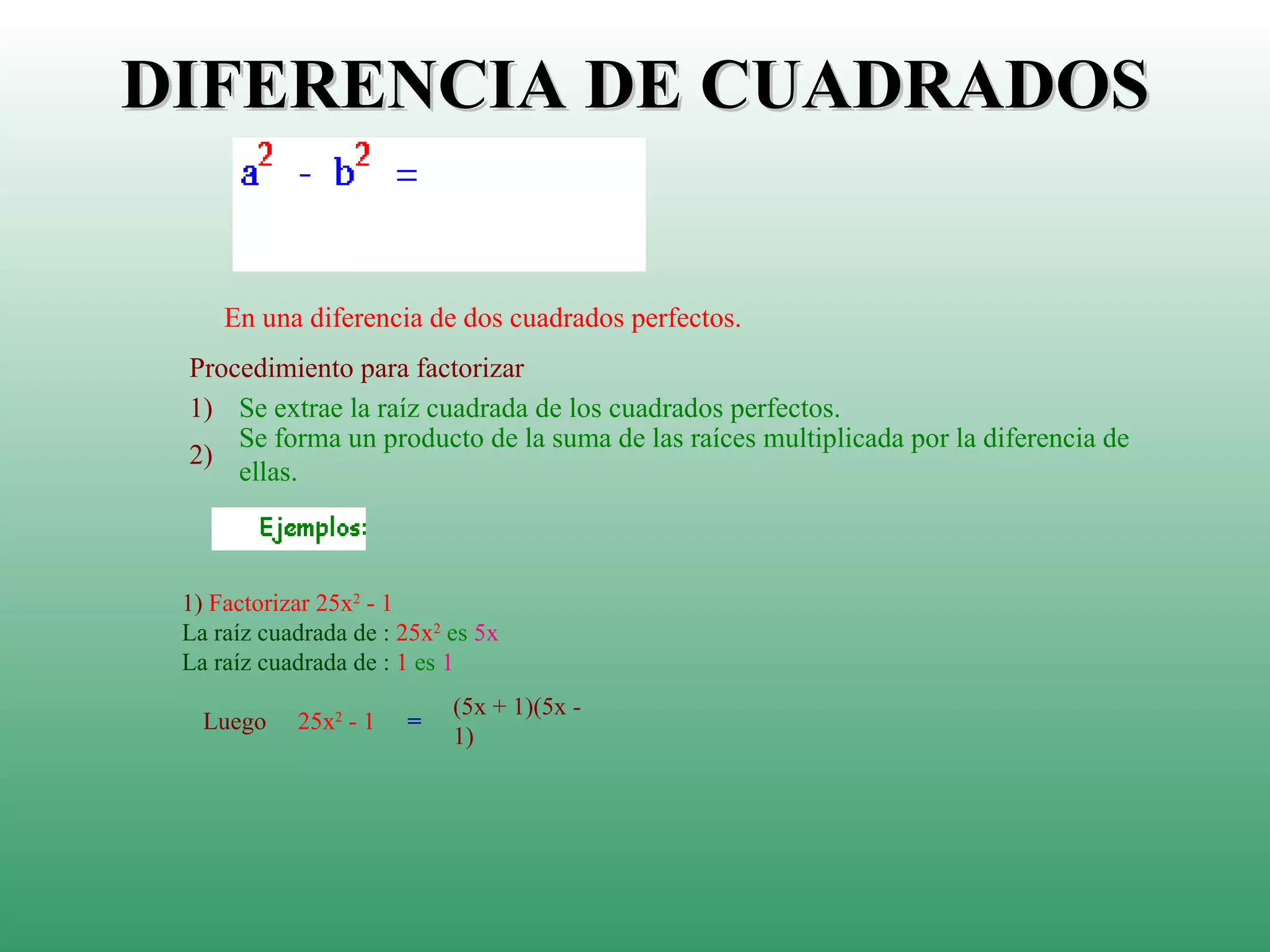
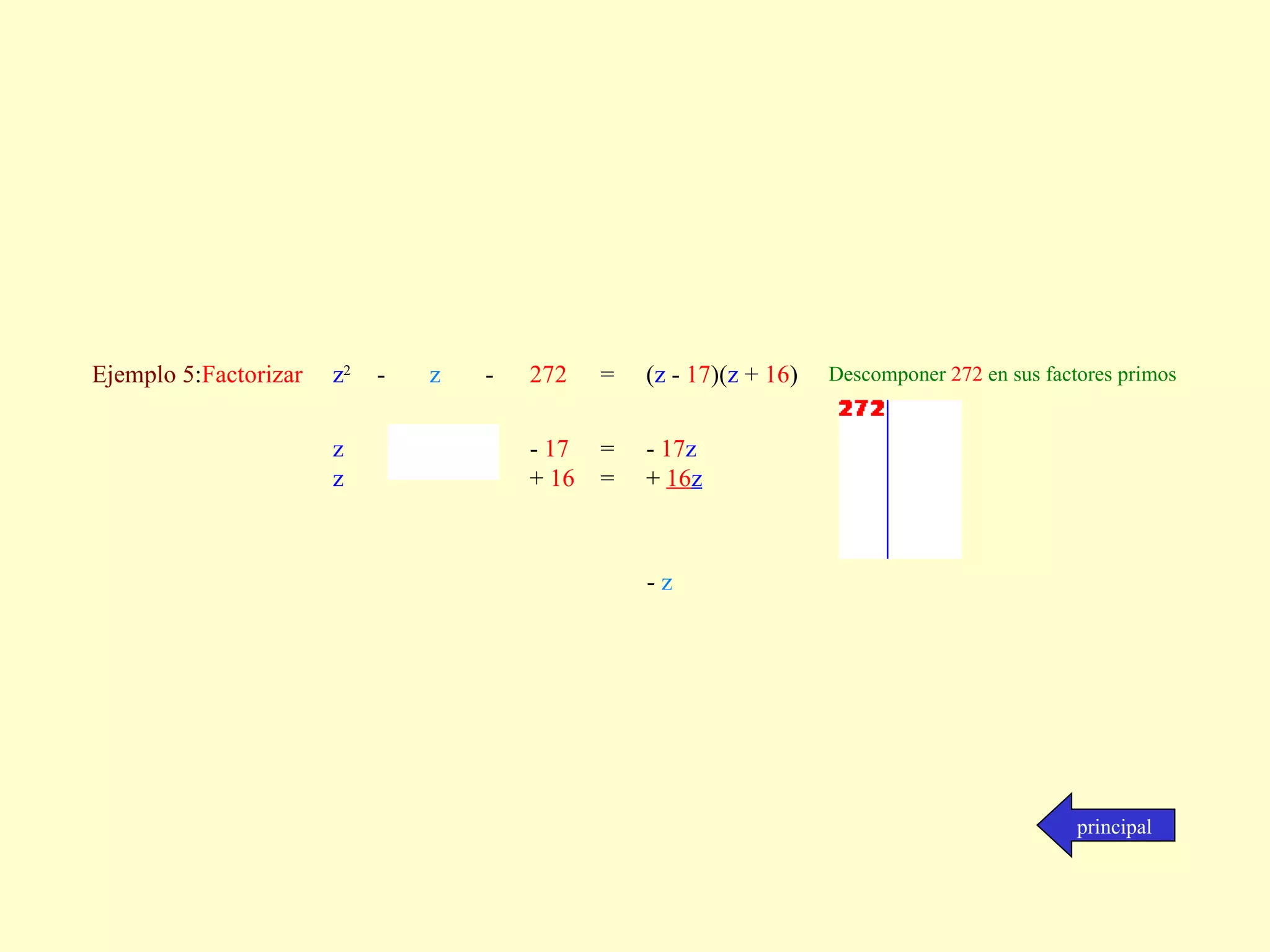
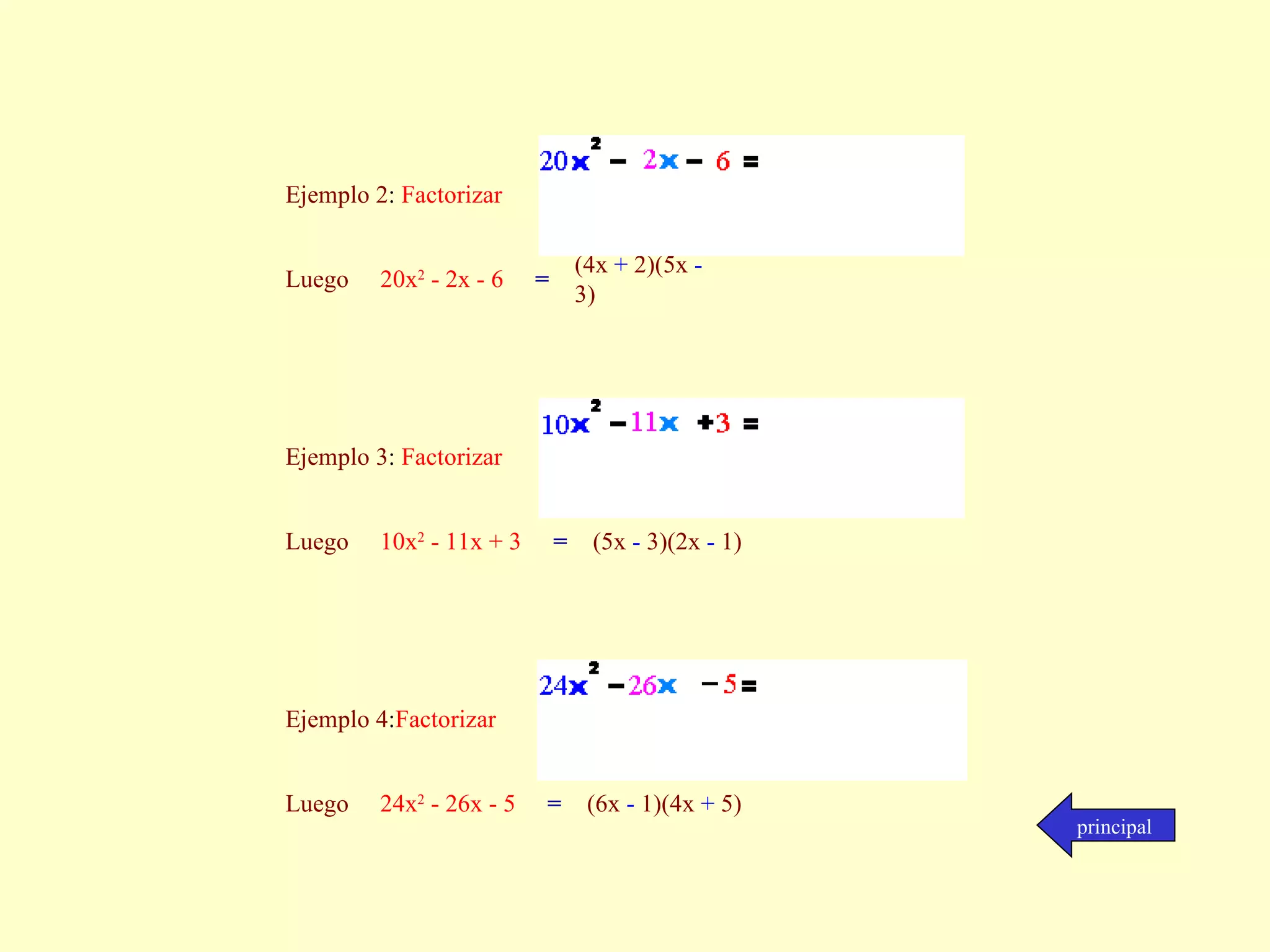
El documento resume diferentes métodos para factorizar polinomios. Explica cómo factorizar cuando el factor común es un monomio o polinomio, así como trinomios de la forma ax^2 + bx + c y diferencias de cuadrados. Proporciona ejemplos para ilustrar cada método de factorización.

1. Factor común Trinomio de cuadrado perfecto Trinomio de la forma: ax2+bx+c Trinomio de la forma: x2+bx+c Diferencia de cuadrados FACTORIZACIÓN

2. FACTOR COMÚN MONOMIO Cuando el factor común a todos los términos del polinomio es un monomio . 1) Factorizar a 9 + 7a M.C.D. (1, 5) = 1 Variable común con su menor exponente: a Factor común monomio: a Entonces: a 9 + 7a = a (a 8 + 7) principal a b + a c + a d = a ( b + c + d ) Procedimiento para factorizar 1) Se extrae el factor común de cualquier clase, que viene a ser el primer factor. 2) Se divide cada parte de la expresión entre el factor común y el conjunto viene a ser el segundo factor. a 9 + 7a Luego se divide --------- = a 8 + 7 a

3. 2 ) : Factorizar 4a 10 + 8a 3 M.C.D. (4, 8) = 4 Variable común con su menor exponente: a 3 Factor común monomio: 4a 3 Entonces: 4a 10 + 8a 3 = 4a 3 (a 7 + 2) principal 4a 10 + 8a 3 Luego se divide ------------ = a 7 + 2 4a 3

4. FACTOR COMÚN POLINOMIO Cuando el factor común que aparece es un polinomio . Procedimiento para factorizar 1 ) : Factorizar (2a - 3)(y + 1) - y - 1 Arreglando = (2a - 3)(y + 1) - (y + 1) Factor común con su menor exponente: (y + 1) Entonces: (2a - 3)(y + 1) - y - 1 = (y + 1) (2a - 4) c (a + b) + d (a + b) + e (a + b) = (a + b) ( c + d + e ) 1) Se extrae el factor común de cualquier clase, que viene a ser el primer factor. 2) Se divide cada parte de la expresión entre el factor común y el conjunto viene a ser el segundo factor. (2a - 3)(y + 1) - (y + 1) Luego se divide ----------------------------- = (2a - 3) - 1 = 2a - 3 - 1 = 2a - 4 (y + 1)

5. 3) : Factorizar (a + 1) 2 (y + 1) - (a + 1)(y + 1) 2 Factor común con su menor exponente: (a + 1)(y + 1) Entonces: (a + 1) 2 (y + 1) - (a + 1)(y + 1) 2 = (a + 1)(y + 1) (a - y) principal (a + 1) 2 (y + 1) - (a + 1)(y + 1) 2 Luego se divide --------------------------------------- = (a + 1) - (y + 1) = (a + 1 - y - 1) = (a - y) (a + 1)(y + 1)

6. FACTORIZACIÓN POR AGRUPACIÓN DE TÉRMINOS Cuando el factor común a todos los términos del polinomio es un polinomio . Procedimiento para factorizar 1. Se trata de agrupar con la finalidad de obtener en primer lugar un factor común monomio y como consecuencia un factor común polinomio. 2. Se divide cada parte de la expresión entre el factor común y el conjunto viene a ser el segundo factor. 2) : Factorizar 2x 2 - 4xy + 4x - 8y Agrupamos ( 2x 2 - 4xy ) + ( 4x - 8y ) Factor común en cada binomio: 2x(x - 2y) + 4(x - 2y) Factor común polinomio: (x - 2y) a x + b x + a y + b y = (a + b ) ( x + y ) 2x(x - 2y) + 4(x - 2y) Luego se divide -------------------------- = 2x + 4 (x - 2y)

7. Entonces: 2x 2 - 4xy + 4x - 8y = (x - 2y) (2x + 4) 3) : Factorizar 2 m+n + 8 m+n + 2 m 8 m + 2 n 8 n Agrupamos ( 2 m+n + 2 m 8 m ) + ( 8 m+n + 2 n 8 n ) Factor común en cada binomio: 2 m ( 2 n + 8 m ) + 8 n ( 8 m + 2 n ) Factor común polinomio: ( 2 n + 8 m ) Entonces: 2 m+n + 8 m+n + 2 m 8 m + 2 n 8 n = ( 2 n + 8 m ) (2 m + 8 n ) principal 2 m ( 2 n + 8 m ) + 8 n ( 8 m + 2 n ) Luego se divide ------------------------------------ = 2 m + 8 n ( 2 n + 8 m )

8. DIFERENCIA DE CUADRADOS En una diferencia de dos cuadrados perfectos. Procedimiento para factorizar 1) Factorizar 25x 2 - 1 La raíz cuadrada de : 25x 2 es 5x La raíz cuadrada de : 1 es 1 1) Se extrae la raíz cuadrada de los cuadrados perfectos. 2) Se forma un producto de la suma de las raíces multiplicada por la diferencia de ellas. Luego 25x 2 - 1 = (5x + 1)(5x - 1)

9. 2) Factorizar 16x 2 - 36y 4 La raíz cuadrada de : 16x 2 es 4x La raíz cuadrada de : 36y 4 es 6y 2 3) Factorizar 121a 2 b 4 c 8 - 144d 10 e 14 La raíz cuadrada de : 121a 2 b 4 c 8 es 11ab 2 c 4 La raíz cuadrada de : 144d 10 e 14 es 12d 5 e 7 principal Luego 16x 2 - 36y 4 = (4x + 6y 2 )(4x - 6y 2 ) Luego 121a 2 b 4 c 8 - 144d 10 e 14 = (11ab 2 c 4 + 12d 5 e 7 )(11ab 2 c 4 - 12d 5 e 7 )

10. TRINOMIO DE CUADRADO PERFECTO Procedimiento para factorizar a 2 + 2ab + b 2 = (a + b) 2 a b En un trinomio cuadrado perfecto. Regla para conocer si un trinomio es cuadrado perfecto. 1) Un trinomio ordenado con relación a una letra 2) Es cuadrado perfecto cuando el primer y tercer término son cuadrados perfectos 3) El segundo término es el doble producto de sus raíces cuadradas . 1) Se extrae la raíz cuadrada del primer y tercer término; en el ejemplo a y b . 2) Se forma un producto de dos factores binomios con la suma de estas raíces; entonces ( a + b )( a + b ). 3) Este producto es la expresión factorizada ( a + b ) 2 .

11. Si el ejercicio fuera así: Procedimiento para factorizar Ejemplo 1 : Factorizar x 2 + 10x + 25 La raíz cuadrada de : x 2 es x La raíz cuadrada de : 25 es 5 El doble producto de las raíces: 2(x)(5) es 10x a 2 - 2ab + b 2 = (a - b) 2 a b 1) Se extrae la raíz cuadrada del primer y tercer término; en el ejemplo a y b . 2) Se forma un producto de dos factores binomios con la diferencia de estas raíces; entonces ( a - b )( a - b ). 3) Este producto es la expresión factorizada ( a - b ) 2 Luego x 2 + 10x + 25 = (x + 5) 2

12. Ejemplo 2 : Factorizar 49y 2 + 14y + 1 La raíz cuadrada de : 49y 2 es 7y La raíz cuadrada de : 1 es 1 El doble producto de las raíces: 2(7y)(1) es 14y Ejemplo 3 : Factorizar 81z 2 - 180z + 100 La raíz cuadrada de : 81z 2 es 9z La raíz cúbica de : 100 es 10 El doble producto de las raíces: 2(9z)(10) es 180z principal Luego 49y 2 + 14y + 1 = (7y + 1) 2 Luego 81z 2 - 180z + 100 = (9z - 10) 2

13. TRINOMIO DE LA FORMA: x2+bx+c Regla para conocer si es un trinomio de la forma x 2 + bx + c. 1. El coeficiente del primer término es 1. 2. El primer término es una letra cualquiera elevada al cuadrado. 3. El segundo término tiene la misma letra que el primero con exponente 1 y su coeficiente es una cantidad cualquiera, positiva o negativa. x 2 + b x + c = ( x + d )( x + e ) Procedimiento para factorizar x x d e = = d x e x 1) Se extrae la raíz cuadrada del 1er. término; aquí, x . 2) Dos números d , e , tales que multiplicados den " c ". b x 3) Sumados resulten " b " ( d + e = b ). 4. El tercer término es independiente de la letra que aparece en el 1° y 2° términos y es una cantidad cualquiera, positiva o negativa.

14. Ejemplo 1 : Factorizar Luego x 2 + 6x + 8 = (x + 4)(x + 2) Ejemplo 2 : Factorizar y 2 - 13 y + 40 = ( y - 8 )( y - 5 ) y y - 8 - 5 = = - 8 y - 5 y - 13 y Luego y 2 - 13y + 40 = (y - 8)(y - 5)

15. principal Ejemplo 5 : Factorizar z 2 - z - 272 = ( z - 17 )( z + 16 ) Descomponer 272 en sus factores primos z z - 17 + 16 = = - 17 z + 16 z - z

16. TRINOMIO DE LA FORMA: ax2+bx+c Procedimiento para factorizar 1) Se traza un aspa entre los términos, ax 2 y c . 2) Se descompone en los extremos del aspa los coeficientes a y c . 3) Se comprueba el término que falta con el producto es aspa, " b " ( d g + e f = b ). Ejemplo 1 : Factorizar Luego 6x 2 + 13x + 6 = (3x + 2)(2x + 3)

17. principal Ejemplo 2 : Factorizar Luego 20x 2 - 2x - 6 = (4x + 2)(5x - 3) Ejemplo 3 : Factorizar Luego 10x 2 - 11x + 3 = (5x - 3)(2x - 1) Ejemplo 4 : Factorizar Luego 24x 2 - 26x - 5 = (6x - 1)(4x + 5)

18. FIN