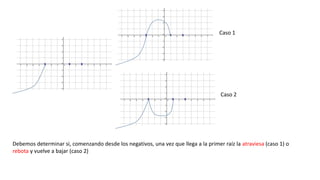
El documento describe las funciones polinómicas. Explica que son funciones cuya fórmula es un polinomio de grado mayor que 2. Para representarlas gráficamente, siempre hay que factorizarlas para encontrar sus raíces. Luego, se utilizan los intervalos determinados por las raíces y el signo de la función en un punto de cada intervalo para saber si la gráfica comienza desde arriba o abajo. Finalmente, de acuerdo al orden de multiplicidad de cada raíz, se determina si la gráfica atraviesa o rebota en

1. Funciones polinómicas
• Repaso rápido de otras funciones estudiadas
• Definición
• Grafico aproximado

2. Que funciones conocemos?
• Función lineal
Su ecuación general es y= ax+b.
Es una ecuación de grado 1
Su representación grafica es una recta
Ejemplo Y=5x+1 pendiente=5 ordenada al origen=1

3. • Funcion cuadrática
Su ecuación general es: y= a𝑥2 + 𝑏𝑥 + 𝑐
Es una ecuación de grado 2
Su representación grafica es una parábola
Ejemplo: y=𝑥2 + 3𝑥 − 1

4. Función polinómica
• Es una función cuya formula es un polinomio de grado mayor que 2
• Para poder representarla gráficamente debemos SIEMPRE factorizarla y asi
poder encontrar sus raíces.
Ejemplo:
𝑓 𝑥 = 𝑥3
− 𝑥2
− 9𝑥 + 9 es una función polinómica de grado 3
si la factorizamos encontraremos 3 raíces
𝑥 − 3 𝑥 + 3 𝑥 − 1
Sus raíces están en 𝑥1 = 3 𝑥2= -3 𝑥3 = 1
Son tres raíces de orden 1. (exponente al que esta elevado cada paréntesis)

5. Son esos tres puntos donde la función pasara por el eje x
Luego deberemos armar los intervalos determinados por esas raíces:
−∞; −3
−3; 1
1; 3
3; +∞
Tomaremos un punto cualquiera perteneciente al PRIMER intervalo
En el intervalo −∞; −3 hay infinitos valores posibles. Tomaremos uno cualquiera.
Por ejemplo x=-20
Debemos reemplazar el valor elegido en la función factorizada para poder analizar el SIGNO que tendrá la función.
De ser positivo sabremos que nuestro grafico comenzará “desde arriba”. Si fuera negativo vendrá “desde abajo”

6. Función factorizada: F(x)= 𝑥 − 3 𝑥 + 3 𝑥 − 1
Intervalos:
−∞; −3 x=-20 (valor elegido) F(-20)= −20 − 3 −20 + 3 −20 − 1
−3; 1
1; 3 que valor toma la función para x=-20
3; +∞
-23 -17 -21
esta multiplicación no importa cuanto
da pero si sabemos que da negativo
- . - . - = -
Esto quiere decir que mi función debo comenzar a dibujarla “viniendo ” de
abajo.

7. Debemos determinar si, comenzando desde los negativos, una vez que llega a la primer raíz la atraviesa (caso 1) o
rebota y vuelve a bajar (caso 2)
Caso 1
Caso 2

8. • Utilizaremos el siguiente criterio:
• Si una raíz tiene orden impar (ver diapositiva 3) la grafica atraviesa
por la raíz
• Si una raíz tiene orden de multiplicidad par, la grafica rebota en esa
raíz.
F(x)= 𝑥 − 3 𝑥 + 3 𝑥 − 1
𝑥1 = 3 𝑚𝑢𝑙𝑡𝑖𝑝𝑙𝑖𝑐𝑖𝑑𝑎𝑑 𝑖𝑚𝑝𝑎𝑟: 𝑎𝑡𝑟𝑎𝑣𝑖𝑒𝑠𝑎
𝑥2= -3 𝑚𝑢𝑙𝑡𝑖𝑝𝑙𝑖𝑐𝑖𝑑𝑎𝑑 𝑖𝑚𝑝𝑎𝑟: 𝑎𝑡𝑟𝑎𝑣𝑖𝑒𝑠𝑎
𝑥3 = 1 multiplicidad impar: atraviesa

9. ¿cuáles serían las raíces y que orden de multiplicidad podría tener cada una?