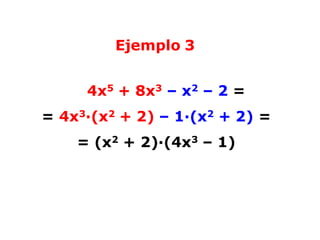Incrustar presentación
Descargar como PDF, PPTX





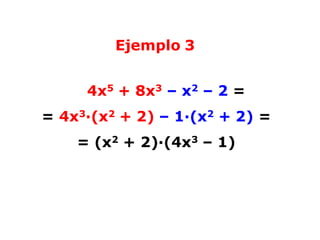



El documento explica cómo aplicar el método de factor común en grupos para factorizar polinomios. Este método involucra separar los términos del polinomio en grupos y extraer el factor común de cada grupo, para luego extraer el factor común común entre los grupos resultantes. El documento ilustra este método a través de seis ejemplos de factorización de polinomios.