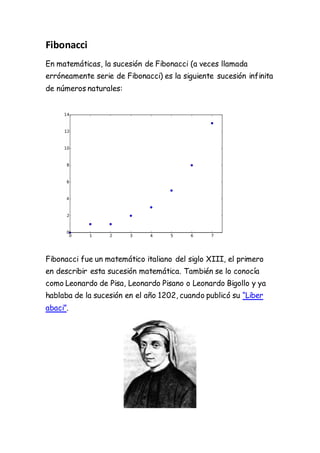
Fibonacci fue un matemático italiano del siglo XIII que describió por primera vez la sucesión de Fibonacci, en la que cada número es la suma de los dos anteriores. Esta sucesión se encuentra en muchos patrones naturales como la espiral de los girasoles y las piñas. La sucesión de Fibonacci tiene muchas propiedades interesantes y amplias aplicaciones en matemáticas.

1. Fibonacci
En matemáticas, la sucesión de Fibonacci (a veces llamada
erróneamente serie de Fibonacci) es la siguiente sucesión infinita
de números naturales:
Fibonacci fue un matemático italiano del siglo XIII, el primero
en describir esta sucesión matemática. También se lo conocía
como Leonardo de Pisa, Leonardo Pisano o Leonardo Bigollo y ya
hablaba de la sucesión en el año 1202, cuando publicó su “Liber
abaci”.

2. Fibonacci era hijo de un comerciante y se crió viajando, en un
medio en donde las matemáticas eran de gran importancia,
despertando su interés en el cálculo.
Se dice que sus conocimientos en aritmética y matemáticas
crecieron enormemente con los métodos hindúes y árabes que
aprendió durante su estancia en el norte de África y luego de
años de investigación, Fibonacci dió con interesantes avances.
Algunos de sus aportes se refieren a la geometría, la aritmética
comercial y los números irracionales, además de haber sido vital
para desarrollar el concepto del cero.
La espiral de Fibonacci: una aproximación de la espiral
áurea generada dibujando arcos circulares conectando las
esquinas opuestas de los cuadrados ajustados a los valores de la
sucesión; adosando sucesivamente cuadrados de lado 0, 1, 1, 2, 3,
5, 8, 13, 21 y 34.
De hecho, cuanto más grandes los números de Fibonacci, más
cerca está la aproximación.

3. Fibonacci ha pasado a la historia por su famosa sucesión, la cual
representa un buen número de situaciones prácticas upongamos
una pareja de conejos, los cuales pueden tener descendencia una
vez al mes a partir 1 – 1 – 2 – 3 – 5 – 8 – 13 – 21 – 34 – 55 – 89 -
144- ....... pero la más anecdótica es la relacionada con una teórica
cría de conejos en una granja.
Supongamos una pareja de conejos, los cuales pueden tener
descendencia una vez al mes a partir del segundo mes de vida.
Suponemos asimismo que los conejos no mueren y que cada
hembra produce una nueva pareja (conejo, coneja) cada mes. La
pregunta es, ¿cuántas parejas de conejos existen en la granja al
cabo de n meses?.
El número de parejas coincide con los términos de la sucesión de
Fibonacci.
La sucesión de Fibonacci es uno de los temas más sorprendentes
de la Matemática, existen multitud de aplicaciones en los que
aparece esa sucesión, existiendo una amplísima bibliografía

4. dedicada exclusivamente al estudio de sus propiedades y
aplicaciones.
Curiosidades de la sucesión de Fibonacci:
 Dos números de Fibonacci consecutivos cualesquiera son
siempre primos entre sí.
 En los girasoles, las semillas se distribuyen en forma de
espirales logarítmicas, unas en sentido horario y otras en
sentido antihorario, si contamos el número de espirales que
hay en un sentido y las que hay en el otro aparecen
términos de Fibonacci consecutivos.
 Si tomas dos números de Fibonacci consecutivos, su
cociente está muy cerca de la razón aúrea "φ" que tiene el
valor aproximado 1.618034...
 Las margaritas también obedecen a esta secuencia, y
acomodan sus semillas en forma de 21 y 34 espirales.
Las piñas, prácticamente cualquier variedad que
encuentres, también presentan un número de espirales que
coincide con dos términos de la sucesión de los números de
Fibonacci, por lo general 8 y 13 o 5 y 8.
 A una escala mucho mayor, los brazos en espiral de las
galaxias también se acomodan según los números
de Fibonacci.

5.  En el triángulo de Tartaglia (Pascal) sumando los términos
de las diagonales secundarias, obtenemos los términos de la
sucesión de Fibonacci, tal como se observa en la figura.
 La suma de diez elementos consecutivos cualesquiera de la
sucesión de Fibonacci es igual a 11 veces, el 7º elemento de
ese grupo.¡OJO!. No hay que comenzar necesariamente por
el primer término de la sucesión.
1 – 1 – 2 – 3 – 5 – 8 – 13 – 21 – 34 – 55 – 89 – 144 - 233 .......
1+1+2+3+5+8+13+21+34+55 = 143 = 11 x 13
 Usando los términos de la sucesión de Fibonacci podemos
dibujar rectángulos de dimensiones iguales a los términos
de la sucesión, expresadas, por ejemplo, en centímetros
13x21
8x13
5x8
3x5
2x3