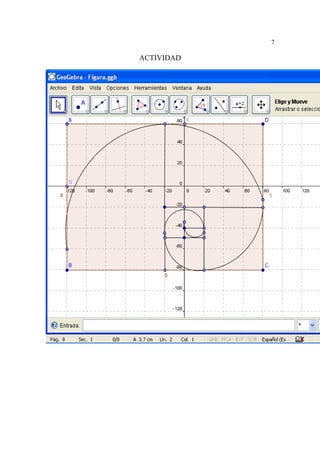
Este documento presenta información sobre el número áureo y la serie de Fibonacci. Explica que el número áureo surge de partir un segmento en dos partes cuya proporción es constante, y que la serie de Fibonacci es una sucesión donde cada número es la suma de los dos anteriores. También describe la relación entre estos conceptos matemáticos y su presencia en la naturaleza, como en la disposición de hojas, flores y ramas de árboles.

1. Escuela Secundaria Técnica 118
Materia: Matemáticas
Tema: El número áureo y la serie de Fibonacci
Profesor: Luís Miguel Villarreal Matias
Alumno: Carlos Ivan Flores Gutiérrez
Grado y Grupo: 3° “A”
Fecha de entrega: 25-Octubre-2012

2. INDICE
Introducción………………………………………………………………….3
Contenido…………………………………………………………………….4-6
Conclusión……………………………………………………………………7
Actividad……………………………………………………………………...8

3. INTRODUCCION
En el siguiente trabajo presentare una pequeña referencia del numero áureo y la serie de
Fibonacci y como se relacionan entre los dos pero también como estos se relacionan en
la naturaleza y la vida cotidiana.
Espero sea de su agrado este trabajo.
3

4. CONTENIDO
Numero áureo:
¿Que es el numero áureo?
El número áureo es el valor numérico de la proporción que guardan entre sí dos
segmentos de recta a y b que cumplen la siguiente relación:
El segmento menor es b. El cociente es el valor del número áureo: φ.
Surge al plantear el problema geométrico siguiente: partir un segmento en otros dos, de
forma que, al dividir la longitud total entre el mayor, obtengamos el mismo resultado
que al dividir la longitud del mayor entre la del menor.
Cálculo del valor del número áureo Dos números a y b están en proporción áurea si se
cumple:
Si al número menor (b) le asignamos el valor 1, la igualdad será:
Multiplicando ambos miembros por a, obtenemos:
Igualamos a cero:
La solución positiva de la ecuación de segundo grado es:
Que es el valor del número áureo, equivalente a la relación .
4

5. Serie de Fibonacci
¿Qué es la serie de Fibonnacci?
En matemática, la sucesión de Fibonacci (a veces mal llamada serie de Fibonacci) es la
siguiente sucesión infinita de números naturales:
La sucesión inicia con 0, y a partir de ahí cada elemento, es la suma de los dos
anteriores (0, 1, 1, 2, 3, 5,8...)
A cada elemento de esta sucesión se le llama número de Fibonacci. Esta sucesión fue
descrita en Europa por Leonardo de Pisa, matemático italiano del siglo XIII también
conocido como Fibonacci. Tiene numerosas aplicaciones en ciencias de la computación,
matemáticas y teoría de juegos. También aparece en configuraciones biológicas, como
por ejemplo en las ramas de los árboles, en la disposición de las hojas en el tallo, en la
flora de la alcachofa y en el arreglo de un cono.
Relación entre el número áureo y la serie de fibonacci
Si se denota el enésimo número de Fibonacci como Fn, y al siguiente número de
Fibonacci, como Fn + 1, descubrimos que, a medida que n aumenta, esta razón oscila, y es
alternativamente menor y mayor que la razón áurea. Podemos también notar que la
fracción continua que describe al número áureo produce siempre números de Fibonacci
a medida que aumenta el número de unos en la fracción. Por ejemplo: ;
;y , lo que se acerca considerablemente al número
áureo. Entonces se tiene que:
Esta propiedad fue descubierta por el astrónomo alemán Johannes Kepler, pero pasaron
más de cien años antes de que fuera demostrada por el matemático inglés Robert
Simson.
A mediados del siglo XIX, el matemático francés Jacques Philippe Marie Binet
redescubrió una fórmula. La fórmula permite encontrar el enésimo número de Fibonacci
sin la necesidad de producir todos los números anteriores. La fórmula de Binet depende
exclusivamente del número áureo:
5

6. El numero áureo en la naturaleza
Como ya lo mencione con anterioridad el numero áureo esta en la
naturaleza y unos ejemplos claros de esto son los que les mostrare a
continuación.
• La disposición de los pétalos de las flores
• La relación entre las nervaduras de las hojas de los árboles
• La relación entre el grosor de las ramas principales y el tronco, o entre las ramas
principales
• La cantidad de espirales de una piña (ocho y trece espirales), flores o
inflorescencias. Estos números son elementos de la sucesión de Fibonacci y el
cociente de dos elementos consecutivos tiende al número áureo.
• En la cantidad de elementos constituyentes de las espirales o dobles espirales de
las inflorescencias, como en el caso del girasol, y en otros objetos orgánicos
como las piñas de los pinos se encuentran números pertenecientes a la sucesión
de Fibonacci. El cociente de dos números sucesivos de esta sucesión tiende al
número áureo.
La serie de Fibonacci en la naturaleza
Los machos de una colmena de abejas tienen un árbol genealógico que cumple con esta
sucesión. El hecho es que un zángano (1), el macho de la abeja, no tiene padre, pero sí
que tiene una madre (1, 1), dos abuelos, que son los padres de la reina (1, 1, 2), tres
bisabuelos, ya que el padre de la reina no tiene padre (1, 1, 2, 3), cinco tatarabuelos (1,
1, 2, 3, 5), ocho tras tatarabuelos (1, 1, 2, 3, 5, 8) y así sucesivamente, cumpliendo con
la sucesión de Fibonacci.

7. 6
CONCLUCION
En este trabajo se mostró lo que es el numero áureo y la serie de Fibonacci para tener
una mejor comprensión del tema así mismo se mostró como se relacionan entre si, y
como se relaciona con la naturaleza, así que estamos en contacto diario con el numero
áureo y la serie de Fibonacci.
Espero haya sido de su agrado este trabajo.

8. 7
ACTIVIDAD