Este documento describe el diseño de un filtro FIR pasabanda a partir de un filtro Butterworth pasabanda en MATLAB. Primero se diseña un filtro Butterworth pasabanda con una banda de paso de 60-200Hz y una banda eliminada de 10-250Hz. Luego, usando los parámetros de orden y frecuencia de corte del filtro Butterworth, se implementa un filtro FIR pasabanda en MATLAB. Finalmente, se grafican las respuestas en frecuencia de ambos filtros para compararlos.

1. FACULTAD DE INGENIERIA ELECTRONICA

2. PROCESAMIENTO DIGITAL DE SEÑALESDISEÑO DE UN FILTRO FIR PASABANDA A PARTIR DE UN FILTRO BUTTERWORTH PASABANDA EN MATLABChristopher LeónQUITO, FEBRERO 2011

3. INTRODUCCIONPara realizar el diseño de un filtro FIR pasabanda, primero vamos a realizar el filtro Butterworth pasabandas ya que de este extraeremos los datos necesarios para la creación del filtro FIR.Como se hace para todo filtro, se partirá de las características que se necesitan de este, las cuales podremos apreciar en el siguiente ejemplo practico.

4. PLANTEAMIENTODiseñar un filtro pasa banda cuya banda de paso vaya de 60Hz hasta 200Hz con menos de 3dB de tolerancia en la banda de paso y 40 dB de atenuación en la banda eliminada, la cual esta a 50 Hz a cada lado de la banda de paso. La frecuencia de muestreo es de 1000Hz.

5. FILTRO BUTTERWORTHDel enunciado anterior podemos extraer los siguientes datos:Frecuencia de muestreo= 1000HzBanda de paso= 60-200HzBanda eliminada= 50Hz a cada lado (10-250Hz)Atenuación banda de paso= menor a 3dBAtenuación banda eliminada= 40dB

6. Código en MATLAB:Primero definimos la frecuencia de muestreo:fm=1000;Ahora calculamos la frecuencia de shannon o NyquistPara esto dividimos la frecuencia de muestreo para 2.fe=fm/2;FILTRO BUTTERWORTH

7. FILTRO BUTTERWORTHBasándonos en esta frecuencia transformamos las frecuencias de la banda de paso y la banda eliminada:Wp=[60 200]/fe;Ws=[10 250]/fe;Ahora colocamos las atenuaciones tanto de la banda de paso como de la banda eliminadaRp=3;Rs=40;

8. FILTRO BUTTERWORTHAhora obtendremos el orden (n) y las frecuencias de corte (Wn) por medio de la función “buttord”[n,Wn]=buttord(Wp,Ws,Rp,Rs)Luego obtenemos los coeficientes del filtro Butterworth con la función “butter”[b,a]=butter(n,Wn);

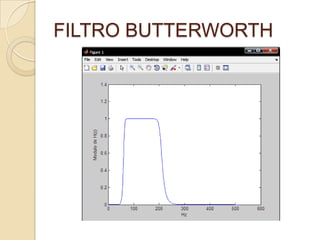
9. FILTRO BUTTERWORTHAhora obtendremos el grafico del modulo de la ganancia compleja.[h,f]=freqz(b,a,[],fm);plot(abs(h))xlabel('Hz')ylabel('Modulo de H(z)')Con lo cual obtenemos el siguiente grafico:

10. FILTRO BUTTERWORTH

11. FILTRO FIRY con esto ha quedado listo nuestro filtro Butterworth pasabanda.Ahora procederemos a implementar el filtro FIR a partir de filtro que diseñamos.

12. FILTRO FIRPara crear el filtro FIR utilizamos el comando FIR1, añadiendo el orden y frecuencias de corte de nuestro filtro anteriorb = fir1(n,Wn);

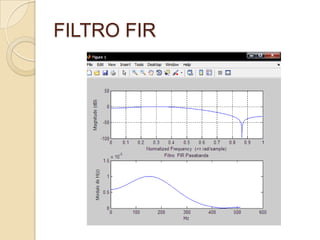
13. FILTRO FIRAhora graficaremos la magnitud del filtro en dB junto con el grafico del modulo de la ganancia compleja.subplot(2,1,1)freqz(b,1,512) subplot(2,1,2)[h,f]=freqz(b,fm)plot(abs(h))xlabel('Hz')ylabel('Modulo de H(z)')title('Filtro FIR Pasabanda')

14. FILTRO FIR

15. FILTRO FIRY con esto queda listo el filtro FIR pasabandas para realizar el proceso de filtrado de nuestras señales.

16. MUCHAS GRACIAS