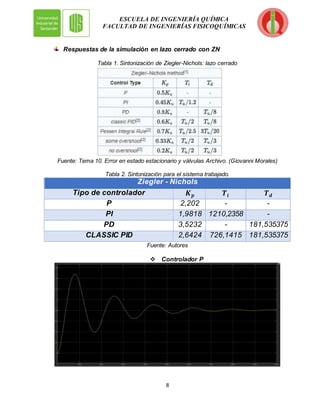
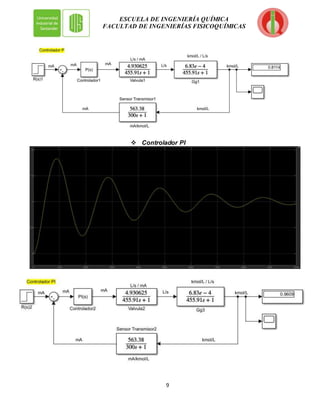
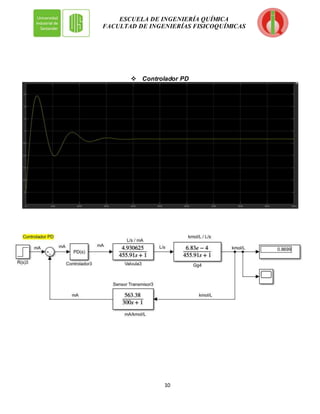
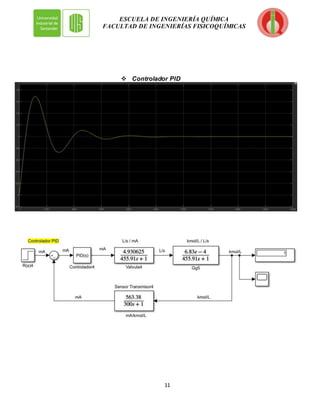
El documento presenta el modelado y simulación de un sistema de control en lazo cerrado para la evaporación de una solución de NaOH. Se incluyen diagramas del proceso y del sistema de control, así como las funciones de transferencia de cada elemento. Adicionalmente, se realizó la sintonización de Ziegler-Nichols para controladores P, PI, PD y PID, y se simularon las respuestas a perturbaciones con cada uno. El documento concluye presentando las conclusiones y recomendaciones del estudio.

1. 1
ESCUELA DE INGENIERÍA QUÍMICA
FACULTAD DE INGENIERÍAS FISICOQUÍMICAS
Asignación Semestral
Segundo Entrega: Evaporación de una solución de 𝑵𝒂𝑶𝑯 para venta comercial a
partir de la caustización del 𝑵𝒂𝑪𝑶𝟑.
Presentado por:
Cristian Jhaidiver Infante Diaz
Nestor Alexis Gómez Celis
Juan Sebastián Suarez Ríos
Presentado a:
Ing. GIOVANNI MORALES MEDINA
Universidad Industrial de Santander-UIS
Control de Procesos Químicos
2022-l

2. 2
ESCUELA DE INGENIERÍA QUÍMICA
FACULTAD DE INGENIERÍAS FISICOQUÍMICAS
 Diagrama del proceso.
Figura 1. Modelado grafico del sistema a realizar estudio
Fuente: Autores
 Diagrama global reducido
Figura 2. Diagrama de bloques reducido.
Fuente: Autores
Función de transferenciaparacontrol Feedback Perturbacionesparalavariable de salida(concentración)

3. 3
ESCUELA DE INGENIERÍA QUÍMICA
FACULTAD DE INGENIERÍAS FISICOQUÍMICAS
𝐶𝐴2 (𝑠) = 𝐺1(𝑠) ∗ 𝐹1 (𝑠) + 𝐺2(𝑠) ∗ 𝐹2 (𝑠)
𝑇5(𝑠) = 𝐺3(𝑠) ∗ 𝐹4(𝑠) + 𝐺4(𝑠) ∗ 𝑇4(𝑠) + 𝐺5(𝑠) ∗ 𝑇2(𝑠)
𝑇2(𝑠) = 𝐺6(𝑠) ∗ 𝐹1(𝑠) + 𝐺7(𝑠) ∗ 𝑇1(𝑠) + 𝐺8(8)∗ 𝐹2(𝑠) + 𝐺9(𝑠) ∗ 𝑇5(𝑠)
𝐹1 ∗
𝐺6
1 − 𝐺5 ∗ 𝐺9
= 𝑇2 ; 𝐺𝑔1 =
𝐺6
1 − 𝐺5 ∗ 𝐺9
𝐹1 ∗ 𝐺1 = 𝐶𝐴2 → 𝐺1 =
𝐶𝐴2
𝐹1
[
𝑘𝑚𝑜𝑙/𝐿
𝐿/𝑠
] ; 𝐺𝑔2 = 𝐺1
𝐹2 ∗
𝐺8
1 − 𝐺5 ∗ 𝐺9
= 𝑇2 ; 𝐺𝑔3 =
𝐺8
1 − 𝐺5 ∗ 𝐺9
𝐹2 ∗ 𝐺2 = 𝐶𝐴2 ; 𝐺𝑔4 = 𝐺2
𝑇1 ∗
𝐺7
1 − 𝐺5 ∗ 𝐺9
= 𝑇2 ; 𝐺𝑔5 =
𝐺7
1 − 𝐺5 ∗ 𝐺9
𝐹4 ∗
𝐺3 ∗ 𝐺9
1 − 𝐺5 ∗ 𝐺9
= 𝑇2 ; 𝐺𝑔6 =
𝐺3 ∗ 𝐺9
1 − 𝐺5 ∗ 𝐺9
𝑇4 ∗
𝐺4 ∗ 𝐺9
1 − 𝐺9 ∗ 𝐺5
= 𝑇2 ; 𝐺𝑔7 =
𝐺4 ∗ 𝐺9
1 − 𝐺9 ∗ 𝐺5
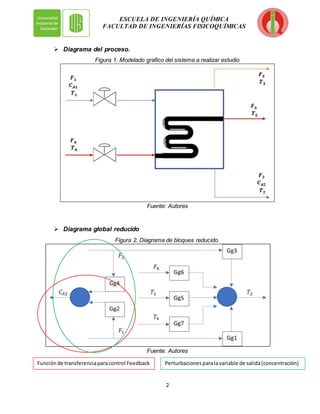
Para la realización del lazo cerrado, se utilizó una función de transferencia global según
el sistema ya establecido y así ejemplificar de forma gráfica, matemática y simulada el
comportamiento de un sistema controlado Feedback respecto a los diversos
controladores utilizados en un sistema de control correctivo.

4. 4
ESCUELA DE INGENIERÍA QUÍMICA
FACULTAD DE INGENIERÍAS FISICOQUÍMICAS
Esquema de control
Figura 3. Modelado grafico del sistema en lazo cerrado (Feedback)
Fuente: Autores
Figura 4. Modelado gráfico simulado en lazo cerrado en Simulink - MATLAB (Feedback)
Fuente: Autores

5. 5
ESCUELA DE INGENIERÍA QUÍMICA
FACULTAD DE INGENIERÍAS FISICOQUÍMICAS
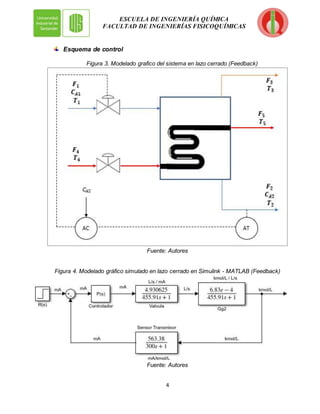
Elementos del lazo de control
 Proceso:
𝐺𝑔2 = 𝐺1 =
6,83∗10−4
455,91𝑠+1
[
𝑘𝑚𝑜𝑙 /𝐿
𝐿/𝑠
], Esta ganancia global se usó para ejemplificar el sistema a
controlar. La figura 2 se hace muestra de cómo se encuentra el sistema con las funciones
globales, entonces se tiene la variable de perturbación (flujo de entrada 1 en L/s), la
ganancia global del proceso y la variable de salida (concentración de hidróxido de sodio
en kmol/L).
𝐺𝑃 (𝑠) = 𝐺𝑔2 = 𝐺1 =
6,83 ∗ 10−4
455,91𝑠 + 1
[
𝑘𝑚𝑜𝑙/𝐿
𝐿/𝑠
]
 Sensor transmisor:
𝐶𝐴10
= 6,6 ∗ 10−3 𝑘𝑚𝑜𝑙𝐴/𝐿
𝐶𝐴20
= 0,035 𝑘𝑚𝑜𝑙𝐴/𝐿
𝐾𝑆𝑇 =
20 − 4
0,035 − 6,6 ∗ 10−3
[
𝑚𝐴
𝑘𝑚𝑜𝑙/𝐿
],
Entonces la ganancia del sensor transmisor es: 𝐾𝑆𝑇 = 563,38[
𝑚𝐴
𝑘𝑚𝑜𝑙 /𝐿
]
𝐻(𝑠) =
563,38
300𝑠 + 1
[
𝑚𝐴
𝑘𝑚𝑜𝑙/𝐿
] 𝑦 𝜏 = 300 [𝑠]
Las unidades de tiempo se hicieron respecto al sistema de unidades del Simulink en
MATLAB.
 Controlador:
𝐺𝐶 (𝑠) = 𝑘𝑐
El comportamiento de este sistema se evaluará respecto a la ganancia ultima para
encontrar el sistema en lazo cerrado con controlador P (proporcional), y así de forma
análoga observar el comportamiento de oscilador armónico conociendo 𝐾𝑢 y 𝑇𝑢, para
definir los parámetros por sintonización de Ziegler – Nichols en lazo cerrado para los tipos
de controladores en sistema ideal.

6. 6
ESCUELA DE INGENIERÍA QUÍMICA
FACULTAD DE INGENIERÍAS FISICOQUÍMICAS
 Válvula:
Se supone un sobredimensionamiento del 100%, también sistema lineal por lo cual
𝑘𝑚𝑘𝑣𝑝𝑘𝑐𝑣 = ±
𝑄𝑀𝐴𝑋
16𝑚𝐴
.
𝑄𝑀𝐴𝑋 = 78,89 [
𝐿
𝑠
], flujo volumétrico del trabajo en el sistema.
𝐾𝑣 =
𝑄𝑀𝐴𝑋
𝑅𝑎𝑛𝑔𝑜 𝑑𝑒 𝐶𝑜𝑟𝑟𝑖𝑒𝑛𝑡𝑒
=
78 ,89
20 −4
= 4,930625 [
𝐿/𝑠
𝑚𝐴
], La válvula usada es para un sistema
Cerrada en Falla, o sea es una válvula de aire para abrir. Ganancia de la válvula positiva.
𝐺𝑉 (𝑠) =
4,930625
455,91𝑠 + 1
[
𝐿/𝑠
𝑚𝐴
]
La constante de tiempo en la válvula se asume igual a la constante de tiempo de la función
de transferencia del proceso para efectos de estudio.
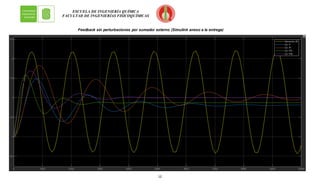
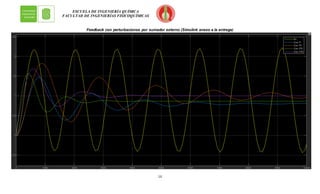
Condición última obtenida por simulación
Gráficamente se tiene: (asumiendo que la ganancia es 𝒌𝒄 = 𝟒,𝟒)

7. 7
ESCUELA DE INGENIERÍA QUÍMICA
FACULTAD DE INGENIERÍAS FISICOQUÍMICAS
Matemáticamente:
1 + 𝐻(𝑆) ∗ 𝐺𝐶 (𝑆) ∗ 𝐺𝑉 (𝑆) ∗ 𝐺𝑃 (𝑆) = 0
1 +
563,38
300𝑠 + 1
∗ 𝑘𝑐 ∗
4,930625
455,91𝑠 + 1
∗
6,83 ∗ 10−4
455,91𝑠 + 1
= 0
(300𝑠 + 1)(455,91𝑠 + 1)(455,91𝑠 + 1) + (563.38)(𝑘𝑐)(4,930625)(6,83 ∗ 10−4) = 0
Polinomio característico:
62356178,43𝑠3
+ 481399,9281𝑠2
+ 1211,82𝑠 + 1 + 1,89725𝑘𝑐 = 0
 ℝ: − 481399,9281𝑤2
+ 1 + 1,89725𝑘𝑐 = 0
 𝕀: − 62356178,43𝑤3
+ 1211,82𝑤 = 0
𝒘𝟐
= 𝟏,𝟗𝟒𝟑𝟑𝟖 ∗ 𝟏𝟎−𝟓
, 𝒘 = 𝟒,𝟒𝟎𝟖𝟑𝟕𝟖 ∗ 𝟏𝟎−𝟑
, 𝑻 =
𝟐𝝅
𝒘
= 𝟏𝟒𝟐𝟓.𝟐𝟖𝟑 [𝒔]
𝒌𝒄 = 𝟒,𝟒𝟎𝟒; 𝑻𝒖 = 𝟏𝟒𝟐𝟓,𝟐𝟖𝟑 𝒚 𝒌𝒖 = 𝟒, 𝟒𝟎𝟒

8. 8
ESCUELA DE INGENIERÍA QUÍMICA
FACULTAD DE INGENIERÍAS FISICOQUÍMICAS
Respuestas de la simulación en lazo cerrado con ZN
Tabla 1. Sintonización de Ziegler-Nichols: lazo cerrado
Fuente: Tema 10. Error en estado estacionario y válvulas Archivo. (Giovanni Morales)
Tabla 2. Sintonización para el sistema trabajado.
Ziegler - Nichols
Tipo de controlador 𝑲𝒑 𝑻𝒊 𝑻𝒅
P 2,202 - -
PI 1,9818 1210,2358 -
PD 3,5232 - 181,535375
CLASSIC PID 2,6424 726,1415 181,535375
Fuente: Autores
 Controlador P

9. 9
ESCUELA DE INGENIERÍA QUÍMICA
FACULTAD DE INGENIERÍAS FISICOQUÍMICAS
 Controlador PI

10. 10
ESCUELA DE INGENIERÍA QUÍMICA
FACULTAD DE INGENIERÍAS FISICOQUÍMICAS
 Controlador PD

11. 11
ESCUELA DE INGENIERÍA QUÍMICA
FACULTAD DE INGENIERÍAS FISICOQUÍMICAS
 Controlador PID

12. 12
ESCUELA DE INGENIERÍA QUÍMICA
FACULTAD DE INGENIERÍAS FISICOQUÍMICAS
Feedback sin perturbaciones por sumador externo (Simulink anexo a la entrega)

13. 13
ESCUELA DE INGENIERÍA QUÍMICA
FACULTAD DE INGENIERÍAS FISICOQUÍMICAS
Feedback con perturbaciones por sumador externo (Simulink anexo a la entrega)

14. 14
ESCUELA DE INGENIERÍA QUÍMICA
FACULTAD DE INGENIERÍAS FISICOQUÍMICAS
Conclusiones
Recomendaciones
Referencias