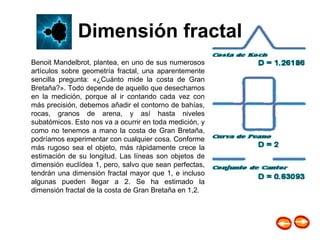
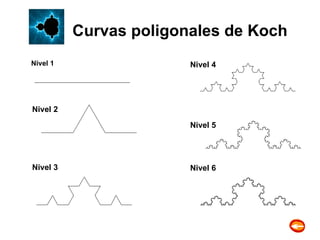
Este documento proporciona una introducción a los fractales, incluyendo una breve historia, la dimensión fractal, ejemplos como las curvas de Koch y el triángulo de Sierpinski, y tipos como funciones iteradas, atractores caóticos y fractales aleatorios.

1. FRACTALES

2. Fractal es… Un poco de historia Dimensión Dimensión fractal Curvas poligonales de Koch Tipos de fractales Funciones iteradas Lindenmayer y Sierpinski Órbitas caóticas Aleatorios y circulares Galería de fractales

3. Fractal es... La palabra fractal es, fundamentalmente, un adjetivo, una característica que, en mayor o menor medida, tienen todos los elementos que poseen forma. Es un concepto matemático acuñado hace bien poco, durante el siglo XX. La razón por la cual un término matemático como éste, ha traspasado las fronteras de los libros de álgebra o geometría, es claramente visual. Algunos algoritmos matemáticos generan imágenes espectaculares. Estas imágenes se conocen también como fractales.

4. Un poco de historia G. Cantor (1845-1918) G. Peano (1858-1932) N. Koch (1815-1897) W. Sierpinski (1882-1969) G. Julia (1893-1978) B. Mandelbrot (1924- )

5. Dimensión La noción "popular" de dimensión no es todo lo correcta que cabría esperar. A menudo se habla de estructuras bidimensionales o tridimensionales equivocadamente. Por ejemplo, una figura formada por las aristas de un cubo (izquierda) es unidimensional. Si está formada por sus caras (derecha) es bidimensional. Sólo si incluye el interior es tridimensional. La confusión reside en que los tres objetos anteriores únicamente pueden visualizarse en un espacio euclídeo de tres dimensiones. Otro ejemplo: la recta 3w=2x=y=4z es unidimensional, pero cualquier intento de dibujarla es ridículo, porque sólo se podría en un espacio de cuatro dimensiones. ¿Alguien vive en algún sitio así..?

6. Dimensión fractal Benoit Mandelbrot, plantea, en uno de sus numerosos artículos sobre geometría fractal, una aparentemente sencilla pregunta: «¿Cuánto mide la costa de Gran Bretaña?». Todo depende de aquello que desechamos en la medición, porque al ir contando cada vez con más precisión, debemos añadir el contorno de bahías, rocas, granos de arena, y así hasta niveles subatómicos. Esto nos va a ocurrir en toda medición, y como no tenemos a mano la costa de Gran Bretaña, podríamos experimentar con cualquier cosa. Conforme más rugoso sea el objeto, más rápidamente crece la estimación de su longitud. Las líneas son objetos de dimensión euclídea 1, pero, salvo que sean perfectas, tendrán una dimensión fractal mayor que 1, e incluso algunas pueden llegar a 2. Se ha estimado la dimensión fractal de la costa de Gran Bretaña en 1,2.

7. Curvas poligonales de Koch Definidas por Helge von Koch en 1904, estas curvas se forman a partir de un segmento, por la sustitución de su tercio central por dos segmentos de longitud tambien un tercio, pero formando ángulos de 60º. Proceso que se repite recursivamente en cada segmento de las figuras que progresivamente se van obteniendo. Ver desarrollo

8. Curvas poligonales de Koch Nivel 1 Nivel 2 Nivel 3 Nivel 4 Nivel 5 Nivel 6

9. Algoritmos de escape Esta figura es un fractal de Mandelbrot. Para cada punto se calculan una serie de valores mediante la repetición de una formula hasta que se cumple una condición, momento en el cual se asigna al punto un color relacionado con el número de repeticiones. Los fractales de este tipo precisan de millones de operaciones, por lo cual sólo pueden dibujarse con la inestimable ayuda del ordenador. Una característica especial del fractal Mandelbrot (y de otros tipos afines) es la de generar un infinito conjunto de fractales, ya que por cada punto se puede generar un fractal tipo Julia, que no es sino una ligera modificación en la fórmula del Mandelbrot. | área fractal | tipos de fractal | 1. Mandelbrot 2. Helecho de Barnsley 3. Triángulo de Sierpinski 4. Atractor de Lorenz 5. Difusión 6. Celular 1. Mandelbrot 2. Helecho de Barnsley 3. Triángulo de Sierpinski 4. Atractor de Lorenz 5. Difusión 6. Celular | index | intro | software | galerías | misc | · área fractal · sysifus, 24 de junio de 1999. · Tipos de fractales

10. El sistema de funciones iteradas (IFS) es un método creado por M. Barnsley, basándose en el principio de autosemejanza. En un fractal IFS siempre se puede encontrar una parte de la figura que guarda una relación de semejanza con la figura completa. Esa relación es a menudo muy difícil de apreciar, pero en el caso del helecho es bastante clara: cualquier hoja es una réplica exacta de la figura completa. Funciones iteradas

11. La idea es sencilla y antigua. Un triángulo en el que se aloja otro, uniendo los puntos medios de cada uno de sus lados. Esto se repite con todos y cada uno de los triángulos formados que tengan la misma orientación que el original, y así sucesivamente. El triángulo de Sierpinski es uno de los pocos fractales que se puede dibujar con exactitud sin ayuda de un ordenador, siguiendo las instrucciones anteriores. Lindenmayer y Sierpinski

12. Cuando estudiamos en el colegio el sistema solar nos dijeron que los planetas describían órbitas elípticas. Como en todo, eso es cierto sólo hasta cierto nivel. El atractor de Lorenz se consigue llevando esa incertidumbre hasta el extremo. La figura siguiente básicamente está formada por un hilo infinitamente largo que va describiendo una trayectoria tridimensional acercándose y alejándose de dos puntos de atracción. Este tipo de modelo nació con un estudio sobre órbitas caóticas desarrollado por E. Lorenz en 1.963. Órbitas caóticas

13. Ciertas categorías de fractal no encajan del todo dentro de las características que hemos descrito en algún otro sitio. Estructuras como el plasma o las imágenes de difusión (figura 1) dependen en cierta medida del azar, por lo cual son únicas e irrepetibles. Los autómatas celulares están en el otro extremo. Funcionan con sencillas reglas que colorean zonas a partir del color de las adyacentes. Pese a que en principio pueda parecer que las imágenes conseguidas con este método vayan a ser sencillas y simétricas, no tiene por qué ser así, como se demuestra en la figura 2. figura 1 figura 2 Aleatorios y circulares

14. Galer í a de fractales