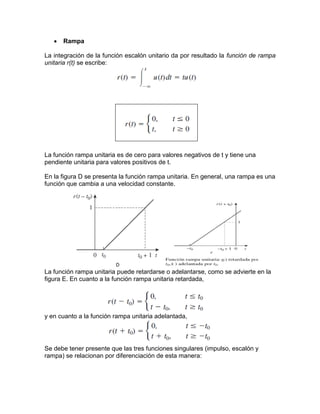
Este documento describe tres funciones singulares comúnmente usadas en análisis de circuitos eléctricos: la función escalón, la función impulso y la función rampa. La función escalón cambia abruptamente de 0 a 1 en un momento dado, la función impulso es la derivada de la función escalón y tiene un valor infinito en un punto, y la función rampa es la integral de la función escalón y tiene una pendiente constante. Estas funciones singulares son herramientas matemáticas útiles para modelar cambios abruptos en tensiones y corrientes en circuitos.

1. REPÚBLICA BOLIVARIANA DE VENEZUELA
INSTITUTO UNIVERSITARIO POLITÉCNICO
“SANTIAGO MARIÑO”
ESCUELA DE INGENERIA INDUSTRIAL
AMPLIACION MARACAIBO
Funciones Singulares
REALIZADO POR:
RINCON CABALLERO ERWIN JOSE
C.I.N°:
20371783
MARACAIBO, MARZO DE 2017

2. CONTENIDO
Funciones singulares.
•Escalón.
•Rampa.
•Impulso.

3. DESARROLLO
Funciones singulares.
Un conocimiento básico de las funciones singulares permitirá dotar de sentido a la
respuesta de circuitos de primer orden a una súbita aplicación de una fuente
independiente de tensión o de corriente de cd. Las funciones singulares (también
llamadas funciones de conmutación) son muy útiles en análisis de circuitos. Sirven
como aproximaciones aceptables de las señales de conmutación que aparecen en
circuitos con operaciones de conmutación. Son de utilidad en la precisa y
compacta descripción de algunos fenómenos de circuitos, especialmente la
respuesta escalón de circuitos RC o RL
Las funciones singulares son discontinuas o tienen derivadas discontinuas. Las
tres funciones singulares de uso más común en análisis de circuitos son las
funciones de escalón unitario, de impulso unitario y de rampa unitaria
•Escalón.
La función de escalón unitario u(t) es de 0 para valores negativos de t y de
1 para valores positivos de t.
En términos matemáticos,
La función escalón unitario está indefinida en t _ 0, donde cambia abruptamente
de 0 a 1. Es adimensional, al igual que otras funciones matemáticas, como seno y
coseno. En la figura A se describe de manera gráfica la función escalón unitario.

4. Si el cambio abrupto ocurre en (donde ) en lugar de t =0, la función
escalón unitario se convierte en:
Lo cual equivale a decir que u(t) se atrasa segundos, como se muestra en la figura
A.), simplemente se remplaza cada t por Si el cambio ocurre en t =- to, la función
escalón unitario se convierte en:
Lo que significa que está adelantada segundo, como se muestra en la figura B
Se usa la función escalón para representar un cambio abrupto de tensión o
corriente, como los cambios que ocurren en los circuitos de sistemas de control y
de computadoras digitales. Por ejemplo, la tensión:
Puede expresarse en términos de la función escalón unitario como:

5. •Impulso.
La derivada de la función escalón unitario es la función ímpulso unitario que se
expresa como:
La función impulso unitario, también conocida como función delta, se muestra en
la figura C
La función impulso unitario es de cero siempre, excepto en t =0,donde está
indefinida.
Las corrientes y tensiones impulsivas ocurren en circuitos eléctricos como
resultado de operaciones de conmutación o fuentes impulsivas. Aunque la función
impulso unitario no es físicamente realizable (lo mismo que las fuentes ideales, los
resistores ideales, etc.), es una herramienta matemática muy útil.
El impulso unitario puede considerarse un choque aplicado o su resultante. Puede
visualizarse como un pulso de área unitaria de muy corta duración. Esto puede
expresarse matemáticamente como:
Donde denota el momento inmediato anterior a t=0 y t=0+
es el momento
inmediato posterior a t=0 Por esta razón, se acostumbra escribir 1 (el cual denota
área unitaria) junto a la flecha que se usa para simbolizar la función impulso
unitario, como en la figura C. El área unitaria se conoce como la fuerza de la
función impulso. Cuando una función impulso tiene una fuerza distinta a la unidad,
el área del impulso es igual a su fuerza.

6.  Rampa
La integración de la función escalón unitario da por resultado la función de rampa
unitaria r(t) se escribe:
La función rampa unitaria es de cero para valores negativos de t y tiene una
pendiente unitaria para valores positivos de t.
En la figura D se presenta la función rampa unitaria. En general, una rampa es una
función que cambia a una velocidad constante.
La función rampa unitaria puede retardarse o adelantarse, como se advierte en la
figura E. En cuanto a la función rampa unitaria retardada,
y en cuanto a la función rampa unitaria adelantada,
Se debe tener presente que las tres funciones singulares (impulso, escalón y
rampa) se relacionan por diferenciación de esta manera:

7. O por integración de este modo:
La función de escalón unitario constituye una manera útil para el modelo del cierre o la apertura de
un interruptor, siempre que se tenga cuidado de vigilar la condiciones iniciales de los circuitos RL o
RC

8. Bibliografía
 Robert L. Boylestad, Louis Nashelsky
 Fundamentos de de Electrónica
 Cuarta edición edit. Person Education.
 Donald L. Schilling, Charles Belove
 Circuitos Electrónicos
 Tercera edición edit. Mc Graw Hill http://es.wikipedia.org