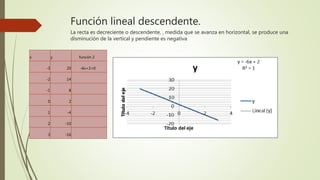
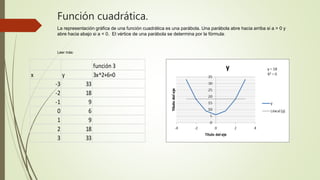
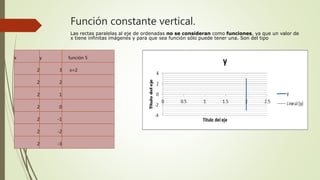
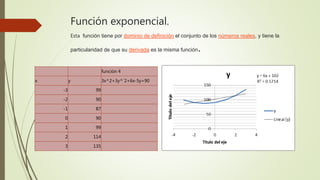
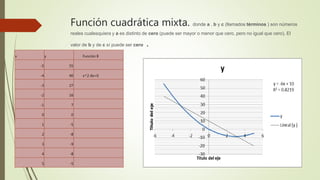
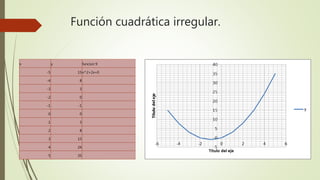
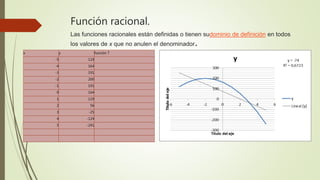
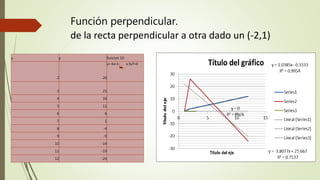
El documento describe 10 tipos diferentes de funciones matemáticas: 1) función lineal ascendente, 2) función lineal descendente, 3) función cuadrática, 4) función constante horizontal, 5) función constante vertical, 6) función exponencial, 7) función cuadrática mixta, 8) función cuadrática irregular, 9) función racional, 10) función perpendicular. Para cada función, se proporcionan ejemplos numéricos que ilustran sus características.

1. FUNCIÓNES .
- GARCÍA GARCÍA DIANA KARINA
- CASTRO ROMERO ESMERALDA
- RODRIGUEZ CALZADA ERNESTO
- CALCULO DIFERENCIAL
- PROFESOR JOSE ERASMO OTLICA LUCERO

2. Función lineal ascendente.
Si la recta es creciente o ascendente , a medida que avanza en horizontal se produce un aumento
de la vertical y su pendiente es positiva.
x y función 1
-3 -3 3x+6=0
-2 0
-1 3
0 6
1 9
2 12
3 15

3. Función lineal descendente.
La recta es decreciente o descendente, , medida que se avanza en horizontal, se produce una
disminución de la vertical y pendiente es negativa.
x y funcón 2
-3 20 -6x+2=0
-2 14
-1 8
0 2
1 -4
2 -10
3 -16

4. Función cuadrática.
La representación gráfica de una función cuadrática es una parábola. Una parábola abre hacia arriba si a > 0 y
abre hacia abajo si a < 0. El vértice de una parábola se determina por la fórmula:
Leer más:
función 3
x y 3x^2+6=0
-3 33
-2 18
-1 9
0 6
1 9
2 18
3 33

5. Función constante horizontal.
aquella función matemática que toma el mismo valor para cualquier valor de la variable
independiente.
x y funciòn 6
3 2y=2
2 2
1 2
0 2
-1 2
-2 2
-3 2

6. Función constante vertical.
Las rectas paralelas al eje de ordenadas no se consideran como funciones, ya que un valor de
x tiene infinitas imágenes y para que sea función sólo puede tener una. Son del tipo
x y función 5
2 3 x=2
2 2
2 1
2 0
2 -1
2 -2
2 -3

7. Función exponencial.
Esta función tiene por dominio de definición el conjunto de los números reales, y tiene la
particularidad de que su derivada es la misma función.
funciòn 4
x y 3x^2+3y^`2+6x-5y+90
-3 99
-2 90
-1 87
0 90
1 99
2 114
3 135

8. Función cuadrática mixta. donde a , b y c (llamados términos ) son números
reales cualesquiera y a es distinto de cero (puede ser mayor o menor que cero, pero no igual que cero). El
valor de b y de c sí puede ser cero .
x y Funciòn 8
-5 55
-4 40 x^2-6x=0
-3 27
-2 16
-1 7
0 0
1 -5
2 -8
3 -9
4 -8
5 -5

9. Función cuadrática irregular.
x y funcion 9
-5 15x^2+2x=0
-4 8
-3 3
-2 0
-1 -1
0 0
1 3
2 8
3 15
4 24
5 35

10. Función racional.
Las funciones racionales están definidas o tienen sudominio de definición en todos
los valores de x que no anulen el denominador.
x y función 7
-5 119
-4 164
-3 191
-2 200
-1 191
0 164
1 119
2 56
3 -25
4 -124
5 -241

11. Función perpendicular.
de la recta perpendicular a otra dado un (-2,1)
y y funcion 10
2 26
y=-5x+1 x-5y7=0
3 21
4 16
5 11
6 6
7 1
8 -4
9 -9
10 -14
11 -19
12 -24