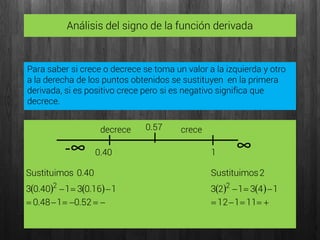
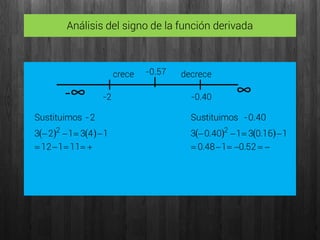
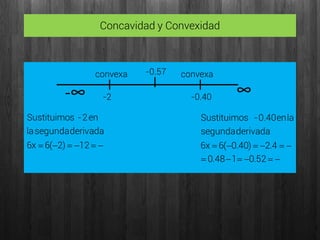
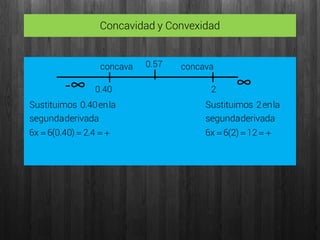
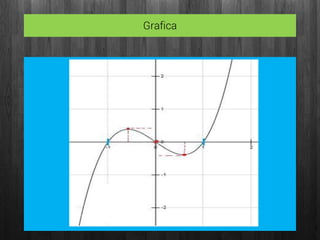
Este documento presenta el análisis de máximos y mínimos de la función f(x)=x3-x. Incluye el cálculo del dominio, asíntotas, puntos de corte con los ejes, puntos críticos analizando la derivada, puntos de inflexión y concavidad/convexidad. Los resultados clave son que la función tiene un mínimo en (-0.57, -0.39) y un máximo en (0.57, 0.39).

1. República Bolivariana de Venezuela
Ministerio del Poder Popular para la Defensa
Universidad Nacional Experimental Politécnica de la Fuerza Armada Nacional
Núcleo Maracay- Sede Aragua
Calculo de Máximos y Mínimos
para la funcion
Integrantes:
Miguel Chacón
Erick Benítez
Williams Arzola
Profesora:
Yasmin Brito
Sección 1SN101
xxy  3

2. Calculo del dominio
El Dominio corresponde a los valores del eje x donde existe
f(x),teniendo en cuenta que y=f(x).
Ya que es una función polinómica su dominio son todos los reales
RyDom:seriaxxyPara 3


3. Calculo de las Asíntotas
Asíntota Vertical: Las asíntotas verticales son rectas verticales a las
cuales la función se va acercando indefinidamente sin llegar nunca
a cortarlas. Son dadas por números que no pertenecen al dominio
de la función, como el dominio de la función son todos los reales
quiere decir que no hay asíntotas verticales.


xx3
x
lim
Asíntota Horizontal: Para calcular la asíntota horizontal hay que
resolver el limite de la función.
Como el resultado es infinito no hay asíntota horizontal

4. Puntos de corte con los ejes
-11x0x x321 
Corte eje x:Para hallar el punto de corte con el eje “x” hacemos y = 0
y resolvemos la ecuación.
 
01)+1)(x-(x
01xx
0xx
xxy
2
3
3





5. Puntos de corte con los ejes
Corte eje y: Para hallar el punto de corte con el eje “y” hacemos x =
0 y resolvemos la ecuación
0y
00y
xxy
3
3




6. Puntos criticos
Derivamos la función xxy 3

1x3xxy 23

57.0x
57.0x
3
3
x
3
1
x
3
1
x1x301x3
0aIgualamos
2
1
22




7. Análisis del signo de la función derivada
Para saber si crece o decrece se toma un valor a la izquierda y otro
a la derecha de los puntos obtenidos se sustituyen en la primera
derivada, si es positivo crece pero si es negativo significa que
decrece.
0.57
-∞ ∞0.40 1
   


11112
143123
2sSustituimo
2
   


52.0148.0
116.03140.03
40.0sSustituimo
2
decrece crece

8. Análisis del signo de la función derivada
-0.57
-∞ ∞-2 -0.40
   


52.0148.0
116.03140.03
0.40-sSustituimo
2
   


11112
143123
2-sSustituimo
2
crece decrece

9. Puntos criticos
39.0y57.018.0y
)57.0()57.0(y
xxy
0.57-sSustituimo
3
3



Para conocer el valor en “y” de los máximos y mínimos se
sustituyen los puntos obtenidos (-0.57 y 0.57) en la función original.
39.0y57.018.0y
)57.0()57.0(y
xxy
0.57sSustituimo
3
3




10. Puntos de inflexion
Para saber si es cóncava o convexa derivamos por segunda vez la
función, igualamos la función derivada por segunda vez a cero y
resolvemos la ecuación.
x61x3y
vezsegundaporDerivamos
2

0x0x6
0aIgualamos


11. Concavidad y Convexidad
-0.57
-∞ ∞-2 -0.40


52.0148.0
4.2)40.0(6x6
derivadasegunda
laen0.40-sSustituimo
 12)2(6x6
derivadasegundala
en2-sSustituimo
convexa convexa

12. Concavidad y Convexidad
0.57
-∞ ∞0.40 2
 12)2(6x6
derivadasegunda
laen2sSustituimo
 4.2)40.0(6x6
derivadasegunda
laen40.0sSustituimo
concava concava

13. Datos para la grafica
0:inflexiondePunto
,0)(-Convexa
)0,(Concava
),57.0(0.57)-,(-Crece
0.57),(-0.57Decrece
0.39)-,P(0.570.57enMinimo
0.39),P(-0.570.57-enMaximo
0:YejeelconCorte
,-1)1,(0:XejeelconCorte
x6y
1x3y
xxy
2
3







14. Grafica