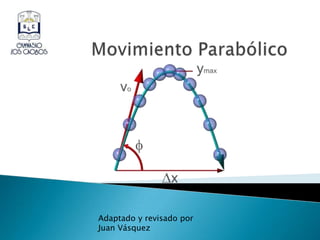
Este documento explica el movimiento parabólico de un proyectil lanzado con cierta velocidad inicial y ángulo. Describe que el movimiento parabólico se compone de movimiento rectilíneo uniforme horizontal y acelerado verticalmente. Presenta ecuaciones para calcular la altura máxima y alcance en función de la velocidad inicial y ángulo. Finalmente, propone varios problemas de aplicación para practicar el cálculo de estas variables.

1. Movimiento ParabólicoAdaptado y revisado por Juan Vásquez

2. El tiro parabólico se puede estudiar como la composición de dos movimientos:Un movimiento rectilíneo uniforme (M.R.U.) en la dirección del eje x.Un movimiento rectilíneo uniformemente acelerado (M.R.U.A.) en la dirección del eje y. ( a = g = 9.8 m/s

3. Diagrama del movimiento

4. Diagrama del movimiento 2

5. En la figura tenemos un proyectil que se ha disparado con una velocidad inicial v0, haciendo un ángulo ϴ con la horizontal, las componentes de la velocidad inicial son:Ecuaciones del Movimiento Parabólico

6. ECUACIONES DEL MOVIMIETO PARABOLICO

7. En el tiro parabólico son de interés la altura máxima y el alcance (o desplazamiento horizontal) conseguido.La altura máxima se alcanza cuando la componente vertical vy de la velocidad se hace cero. Como vy = v0y - gt, se alcanzará la altura máxima cuando t = v0y/g.Utilizando estos datos llegarás fácilmente a la conclusión de que el valor de la altura máxima es:ymax= v0y2/2g = (v02/2g) sen2α

8. El móvil estará avanzando horizontalmente a la velocidad constante v0x durante el tiempo de vuelo, que será 2t(siendo t el tiempo en alcanzar la altura máxima) ya que el móvil tarda lo mismo en subir que en bajar.Por lo tanto el alcance es:Xmax = v0x2t, es deciralcance = Xmax = (v02/g) sen 2α

9. Demostracion virtualhttp://www.educaplus.org/movi/4_3tparabolico.html

10. Problema 1Un avión en vuelo horizontal a una altura de 300 m y con una velocidad de 60 m/s, deja caer una bomba. Calcular el tiempo que tarda en llegar al suelo, y el desplazamiento horizontal de la bomba.Problemas de aplicación

11. Problema 2Se lanza un cuerpo desde el origen con velocidad horizontal de 40 m/s, y con una velocidad vertical hacia arriba de 60 m/s. Calcular la máxima altura y el alcance horizontal.

12. problema 3. Resolver el ejercicio anterior, tomando como lugar de lanzamiento la cima de una colina de 50 m de altura.

13. Problema 4. Se lanza un proyectil desde una colina de 300 m de altura, con una velocidad horizontal de 50 m/s, y una velocidad vertical de -10 m/s (hacia abajo). Calcular el alcance horizontal y la velocidad con que llega al suelo.

14. Problema 5. Un cañón dispara una bala desde lo alto de un acantilado de 200 m de altura con una velocidad de 46 m/s haciendo un ángulo de 30º por encima de la horizontal. Calcular el alcance, el tiempo de vuelo, y las componentes de la velocidad de la bala al nivel del mar. Hallar también la altura máxima. (Hallar primero, las componentes horizontal y vertical de la velocidad inicial).