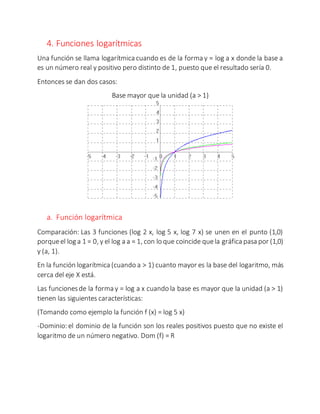
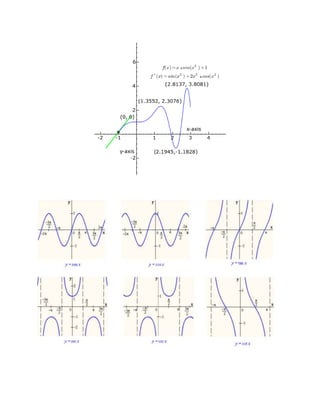
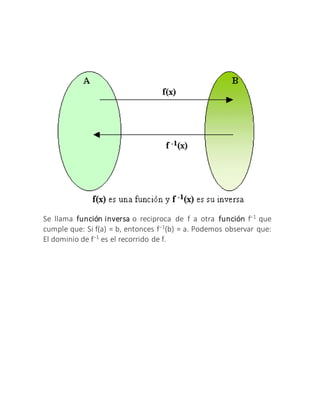
Este documento resume las funciones trascendentes más importantes como las funciones trigonométricas (seno, coseno, tangente, etc.), la función exponencial, las funciones logarítmicas y la función inversa. Describe las propiedades y características de cada función trascendente, incluyendo sus dominios, recorridos y gráficas. También proporciona ejemplos y fórmulas matemáticas para ilustrar cada tipo de función.

1. FUNCIONES TRASCENDENTES.
MICHAEL STEVEN RODRIGUEZ HERNANDEZ
Presentado a:
QUEVIN BARRERA
FUNDACION UNIVERSITARIA DE SAN GIL
INGENIERIA DE SISTEMAS
CALCULO DIFERENCIAL
YOPAL
2017

2. Contenido
1. Clasificación de Funciones Trascendentes
2. Funciones Trigonométricas
a. Seno
b. Coseno
c. Tangente
d. Cotangente
e. Secante
f. Cosecante
3. Funciones Exponencial
a. Propiedades de las Funciones Exponenciales
4. Funciones Logarítmicas
a. Función Logarítmica
5. Función Inversa
6. Bibliografías.

3. 1. FUNCIONES TRASCENDENTES
Las funciones racionales y las irracionales, que han sido tratadas en las páginas
anteriores, se denominan funciones algebraicas.
Las funciones que no son algebraicas se llaman funciones trascendentes.
Son funciones trascendentales elementales
 Función exponencial:
F(x)=ax; a > 0, a ≠ 1.
 Función logarítmica:
F(x)=loga(x); a > 0, a ≠ 1. Es inversa de la exponencial.
 Funciones trigonométricas:
También llamadas circulares:
F(x) =sen(x); f(x) =cos(x); f(x) =tg(x); f(x) =cosec(x); f(x) =sec(x) y f(x) =cotg(x)

4. 2. Funciones trigonométricas
Una función trigonométrica es importante por el hecho de tener un patrón y ser
repetitiva, esto le da la capacidad al que la utiliza de poder interpretar ciertos actos
físicos que requieren de cierta repetitividad para funcionar. Las funciones
trigonométricas más utilizadas son: seno, coseno, tangente, cotangente, secante,
cosecante. Basándonos en lo anterior te dejamos la siguiente tabla que muestra
algunos datos importantes de las funciones trigonométricas más comunes.
Las letras minúsculas son las que utilizamos en el Teorema de Pitágoras, las letras
Mayúsculas, en éste caso, se utilizarán para referirnos a los Ángulos del Triángulo.

5. a. Función Seno (Sen): El dominio de la función seno es el conjunto de todos os
númerosreales los valores pueden ser expresadosen radianes. Para elaborar
la gráfica de la función seno se toma la primera vuelta del círculo unitario.
b. Función Coseno (Cos):
El dominio de la función coseno es el conjunto de todos os númerosreales
los valores pueden ser expresadosen radianes. Para elaborar la gráfica de la
función coseno se toma la primera vuelta del círculo unitario. Recibe el
nombrese cosinusoide.

6. c. Función Tangente (Tan): Ésta Función nos representa la relación entre Lado
adyacente sobre Hipotenusa. Su simbología es la siguiente:
d. Función Cotangente (Cot): Quedescribela relación entre Lado Adyacentecon
Lado Opuesto.

7. e. Función Secante (Sec): Relación entre Hipotenusa sobre Lado Adyacente.
f. Función Cosecante (CsC): Nos muestra la relación entre Hipotenusa sobre
Lado Opuesto:

8. 3. Función Exponencial
En la naturaleza y en la vida social existen numerososfenómenos que se rigen por
leyes de crecimiento exponencial. Tal sucede, por ejemplo, en el aumento de un
capitalinvertido a interéscontinuoo en el crecimiento delaspoblaciones.En sentido
inverso, también las sustanciasradiactivassiguen unaley exponencialen su ritmo de
desintegración para producir otrostipos de átomos y generar energía y radiaciones
ionizantes.
Se llama función exponencial de base a aquella cuya forma genérica es f (x) = ax,
siendo a un número positivo distinto de 1. Por su propia definición, toda función
exponencial tiene por dominio de definición el conjunto de los números reales R.
La funciónexponencialpuedeconsiderarsecomola inversa de la función logarítmica
Representación gráfica de varias funciones exponenciales.

9. a. Propiedades de las funciones exponenciales
Para toda función exponencial de la forma f(x) = ax
, se cumplen las siguientes
propiedades generales:
 La función aplicada al valor cero es siempre igual a 1:
f (0) = a0
= 1.
 La función exponencial de 1 es siempre igual a la base:
F (1) = a1
= a.
 La funciónexponencialde unasuma devaloreses igualalproductodela aplicación
de dicha función aplicada a cada valor por separado.
F (x + x?) = ax+x?
= ax
× ax?
= f (x) × f (x?).
 La función exponencial de una resta es igual al cociente de su aplicación al
minuendo dividida por la función del sustraendo:
F (x - x?) = ax-x?
= ax
/ax?
= f (x)/f (x?).

10. 4. Funciones logarítmicas
Una función se llama logarítmica cuando es de la forma y = log a x donde la base a
es un número real y positivo pero distinto de 1, puesto que el resultado sería 0.
Entonces se dan dos casos:
Base mayor que la unidad (a > 1)
a. Función logarítmica
Comparación: Las 3 funciones (log 2 x, log 5 x, log 7 x) se unen en el punto (1,0)
porqueel log a 1 = 0, y el log a a = 1, con lo que coincide quela gráfica pasa por (1,0)
y (a, 1).
En la función logarítmica (cuando a > 1) cuanto mayor es la base del logaritmo, más
cerca del eje X está.
Las funcionesde la forma y = log a x cuando la base es mayor que la unidad (a > 1)
tienen las siguientes características:
(Tomando como ejemplo la función f (x) = log 5 x)
-Dominio: el dominio de la función son los reales positivos puesto que no existe el
logaritmo de un número negativo. Dom (f) = R

11. En este tramo la función es negativa porque al introducir la anti imagen de un
número racional la imagen que da, es un número negativo, lo que no quiere decir
que existan imágenes para númerosnegativos en esta función, ya que es imposible.
Log -x”
-Recorrido: el recorrido de la función es toda la recta real
Ya que se ve como la función llega de -" y continua hacia +”.
-Continuas y crecientes: la función es creciente en todo su dominio porque...
...x < x’! f(x) " f(x'), ycontinua porquetodos sus puntostienen imagen, tienen límite,
y el límite de un punto coincide con la imagen del punto.
-Simetría: la función no es ni simétrica impar (por no ser simétrica respecto del
origen) ni tampoco par (por no ser simétrica respecto del eje de coordenadas

12. No es simétrica respecto del origen
No es simétrica respecto del eje de ordenadas
-Asíntotas: Partiendo del Dominio de la función (Dom (f) = R+)
No se ven números concretos candidatos a asíntota por lo que viendo la gráfica
deducimos que
x = 0, es una asíntota vertical y al probarlo comprobamos que es cierto.
Lim log 5 x = -”
x! 0 +
Lim log 5 x = +”
X! 0 -
No tiene asíntotas horizontales porqueel limite cuando la función tiende a infinito
no es un número concreto, (a simple vista se aprecia) al igualque no tiene asíntotas
oblicuas.

14. 5. FUNCIONES INVERSAS
Dada una función f(x), su inversa es otra función, designada por f-1
(x)
de forma que se verifica: si f(a) = b, entonces f-1
(b) = a
 Pasos a seguir para determinar la función inversa de una dada:
 Despejar la variable independiente x.
 Intercambiar la x por la y, y la y por la x.
La función así obtenida es la inversa de la función dada.
Las gráficas de dos funciones inversas son simétricas respecto de la
bisectriz del 1.er
cuadrante y del 3.er
cuadrante.
Las funciones f y g son llamadas funciones inversas si:
g(f(x)) = x para cada x en el dominio de f, y
f(g(x)) = x para cada x en el dominio de g.
Cuando f y g son funciones inversas, escribimos g(x) como f−1(x).

15. Se llama función inversa o reciproca de f a otra función f−1
que
cumple que: Si f(a) = b, entonces f−1
(b) = a. Podemos observar que:
El dominio de f−1
es el recorrido de f.

16. BIBLIOGRAFIAS
 https://matematicasiesoja.wordpress.com/2014/05/28/la-funcion-
de-las-funciones/
 http://recursostic.educacion.es/descartes/web/materiales_didactic
os/Procedimiento_analizar_funcion/2bcnst_14_10.htm
 http://calculo.cc/temas/temas_bachillerato/primero_ciencias_soci
ales/funciones_elementales/teoria/exponenciales.html
 http://edumatematicas.pbworks.com/w/file/fetch/67447369/FUN
CIONES%20TRASCENDENTES.pdf