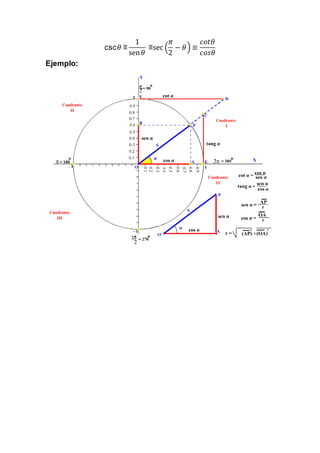
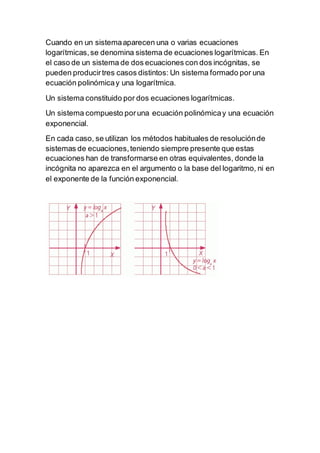
El documento trata sobre funciones trascendentes como las funciones trigonométricas, exponenciales y logarítmicas. Explica las propiedades de estas funciones, incluyendo sus gráficas y derivadas. También cubre temas como ecuaciones y sistemas de ecuaciones que involucran funciones logarítmicas y exponenciales.

1. FUNCIONES TRASCENDENTES
YUMILA SOGAMOSO TARACHE
FUNDACION UNIVERSITARIA UNISANGIL
INGENIERIA DE SISTEMAS
CALCULO DIFERENCIAL
YOPAL-CASANARE
2017

2. FUNCIONES TRASCENDENTES
PRESENTADO A
ING. QUEVIN YOHAN BARRERA
FUNDACION UNIVERSITARIA UNISANGIL
INGENIERIA DE SISTEMAS
CALCULO DIFERENCIAL
YOPAL-CASANARE
2017

3. CONTENIDO
1.FUNCIONES TRASCENDENTES
1.1 EJEMPLOS
2. FUNCIONES TRIGONOMETRICAS
2.2 EQUIVALENCIAS DE RADIANES
2.3 GRAFICA
3. FUNCIONES INVERSAS
3.1 EJEMPLO
4. FUNCIONES EXPONENCIALES
4.1 PROPIEDADES
4.2 DERIVADAS
5. FUNCIONES LOGARITMICA
5.1 ECUACIONES LOGARITMICAS
5.2 SISTEMA DE ECUACIONES LOGARITMICAS

4. Funciones Trascendentes
Son Aquellas funciones que no satisfacen una ecuación polinómica:
con este tipo de funciones la variable independiente se encuentra
como exponente, índice de raíz.
una función de una variable es trascendente si es independiente de
un sentido algebraico
se define por la expresión:
𝑓( 𝑥) = a 𝑥
donde a>0 y a≠1
características
su recorrido es (0+∞)
la función corta en el eje y en (0,1)
el eje x es una asíntota horizontal
ejemplo:5 𝑥
= 50
=1
= 51
=5
= 5−1
=
1
25

5. El logaritmo y la función exponencial son algunos ejemplos de
funciones trascendentes.El término funcióntrascendente amenudo
es utilizado para describira las funciones trigonométricas ya que
también son funciones trascendentes,o sea
el seno, coseno,tangente, cotangente, secante, y la cosecante.
Una función que no pertenece al conjunto de las funciones
trascendentes se dice que es una función algebraica.Ejemplos de
funciones algebraicas son las funciones racionales y la función raíz
cuadrada.
La operaciónde calcular la función primitiva (o integral indefinida)
de una función algebraica es una fuente de funciones
trascendentes.Por ejemplo,la función logaritmo surgió a partir de
la función recíprocaen un intento para calcular el área de un sector
hiperbólico.Por lo tanto el ángulo hiperbólico y las funciones
hiperbólicas senh, cosh, y tanh son todas funciones trascendentes.

6. Función Trigonométrica
son las funciones establecidas con el fin de extender la definiciónde
las razones trigonométricas a todos los números reales y complejos.
las funciones trigonométricas se definen comúnmente como el
cociente entre dos lados de un triangulo rectángulo asociados a
sus ángulos
Las funciones trigonométricas son funciones cuyos valores son
extensiones del concepto de razón trigonométrica en un triángulo
rectángulo trazado en una circunferencia unitaria (de radio unidad).
Definiciones más modernas las describen como series infinitas o
como la solución de ciertas ecuaciones diferenciales, permitiendo
su extensión a valores positivos y negativos, e incluso a números
complejos.
Existen seis funciones trigonométricas básicas. Las últimas cuatro,
se definen en relación de las dos primeras funciones, aunque se
pueden definir geométricamente o por medio de sus relaciones.
Algunas funciones fueron comunes antiguamente, y aparecen en
las primeras tablas, pero no se utilizan actualmente ; por ejemplo
el verseno (1 − cos θ) y la exsecante (sec θ − 1).
equivalencias en radianes
seno 𝜃 ≡
1
csc 𝜃
≡cos (
𝜋
2
− 𝜃) ≡
𝑐𝑜𝑠𝜃
𝑐𝑜𝑡𝜃
cos𝜃 ≡
1
sec 𝜃
≡sen (
𝜋
2
− 𝜃) ≡
𝑠𝑒𝑛𝜃
𝑡𝑎𝑛𝜃
tan 𝜃 ≡
1
cot 𝜃
≡cot(
𝜋
2
− 𝜃) ≡
𝑠𝑒𝑛𝜃
𝑐𝑜𝑠𝜃
cot𝜃 ≡
1
tan 𝜃
≡tan (
𝜋
2
− 𝜃) ≡
𝑐𝑜𝑠𝜃
𝑠𝑒𝑛𝜃
sec𝜃 ≡
1
cos 𝜃
≡csc (
𝜋
2
− 𝜃) ≡
𝑡𝑎𝑛𝜃
𝑠𝑒𝑛𝜃

7. csc𝜃 ≡
1
sen 𝜃
≡sec (
𝜋
2
− 𝜃) ≡
𝑐𝑜𝑡𝜃
𝑐𝑜𝑠𝜃
Ejemplo:

8. Funciones inversas
Dada una función 𝑓( 𝑥), su inversa es otra función, designada por
f−1
(𝑥) de forma que se verifica: si 𝑓( 𝑎) = 𝑏, entonces f−1
(𝑏)=a
pasos a seguir para determinar inversa de una dada
- despejar la variable independiente x
_
Intercambiar la x por la y, y la y por la x.
La función así obtenida es la inversa de la función dada.
-Las gráficas de dos funciones inversas son simétricas
respecto de la bisectriz del 1.er
cuadrante y del 3.er
cuadrante.
Ejemplo

9. Función exponencial
es conocidaformalmente como la función real ex
, donde e es
el número de Euler, aproximadamente 2.71828.;esta función tiene
por dominio de definiciónel conjunto de los números reales, y tiene
la particularidad de que su derivada es la misma función. Se denota
equivalentemente como f(x)=ex
o exp(x), donde e es la base de los
logaritmos naturales y corresponde a la función
inversa del logaritmo natural.
En términos mucho más generales,una función real E(x) se dice
que es del tipo exponencial en base a si tiene la forma
𝐸( 𝑋) = 𝐾. 𝑎 𝑋
La función exponencial ex
puede ser definida de diversas maneras
equivalentes entre sí, como una serie infinita o bien como un límite
de una sucesión.En particular puede ser definidacomo una serie
de potencias
𝑒 𝑥
= ∑(
xn
n!
= 1 + x +
x2
2!
+
x3
3!
+
x4
4!
+ ⋯)
∞
𝑛=0
o como el límite de la sucesión:
𝑒 𝑥
= lim
n→∞
(1 +
x
n
)
n
x=∫
1
𝑡
𝑦
1
𝑑𝑡
Propiedades
La función exponencial (y exponenciales en base distinta a e)
satisfacenlas siguientes propiedades generales.
 Son las únicas funciones que son igual a su derivada
(multiplicada por una constante, en el caso de que tengan una
base distinta a e)
𝑒𝑥𝑝( 𝑥 + 𝑦) = exp( 𝑥). exp⁡( 𝑦)

10. 𝑒𝑥𝑝( 𝑥 − 𝑦) = exp( 𝑥)/exp⁡( 𝑦)
exp(−𝑥) =
1
exp⁡( 𝑥)
exp(0) = 1
Derivadas
La importancia de las funciones exponenciales en matemática y
ciencias radica principalmente de las propiedadesde
su derivada. En particular,
𝑑
𝑑𝑥
𝑒 𝑥
= 𝑒 𝑥
Es decir, ex
es su propia derivada. Es la única función con esa
propiedad (sin tomar en cuenta la multiplicación de la función
exponencial por una constante). Otras formas de expresar lo
anterior:
 La pendiente del gráfico en cualquier punto es la altura de la
función en ese punto.
 La razón de aumento de la función en x es igual al valor de la
función en x.
 La función es solución de la ecuación diferencial 𝑦1
= 𝑦.2
Si la base de la función exponencial es cualquier número
real a mayor que 0, entonces su derivada se puede generalizar así
𝑑
𝑑𝑥
𝑎 𝑥
= 𝑎 𝑥
.ln(𝑎)
donde la función ln(a) es el logaritmo natural de a. En el caso
particular de a = e resulta que ln(e) = 1 y por lo tanto
𝑑
𝑑𝑥
𝑒 𝑥
= 𝑒 𝑥

12. Funciones logarítmicas
Como la exponencial, la función logarítmicase utiliza con asiduidad
en los cálculos y desarrollos de las matemáticas, las ciencias
naturales y las ciencias sociales.Entre otros fines,se usa
ampliamente para "comprimir" la escala de medidade magnitudes
cuyo crecimiento,demasiado rápido,dificulta su representación
visual o la sistematización del fenómeno que representa.
Una función logarítmica es aquella que genéricamente se expresa
como
𝑓( 𝑥) == logaX⁡⁡⁡siendo a la base de esta función, que ha de ser
positiva y distinta de 1.
La función logarítmica es la inversa de la función exponencial
log 𝑎 𝑥 = 𝑏 ⇔ab=x
Ecuaciones logarítmicas
Cuando en una ecuación la variable o incógnita aparece como
argumento o como base de un logaritmo, se llama logarítmica.
La resoluciónde ecuaciones logarítmicas se basa en los mismos
procedimientos utilizados en la resolución de las ecuaciones
habituales. Aunque no existen métodos fijos, habitualmente se
procura convertir la ecuación logarítmica en otra equivalente donde
no aparezca ningún logaritmo. Para ello, se ha de intentar llegar a
una situación semejante a la siguiente:
log 𝑎 𝑓(𝑥) = log 𝑎 𝑔(𝑥)
Sistemas de ecuaciones logarítmicas

13. Cuando en un sistemaaparecen una o varias ecuaciones
logarítmicas,se denomina sistema de ecuaciones logarítmicas. En
el caso de un sistema de dos ecuaciones con dos incógnitas, se
pueden producirtres casos distintos: Un sistema formado por una
ecuación polinómicay una logarítmica.
Un sistema constituido por dos ecuaciones logarítmicas.
Un sistema compuesto poruna ecuación polinómicay una ecuación
exponencial.
En cada caso, se utilizan los métodos habituales de resoluciónde
sistemas de ecuaciones,teniendo siempre presente que estas
ecuaciones han de transformarse en otras equivalentes, donde la
incógnita no aparezca en el argumento o la base del logaritmo, ni en
el exponente de la función exponencial.