Geoestadistica lineal

GEOESTADÍSTICA Geoestadística Lineal
1
CURSO DE GEOESTADISTICA INGENIERIA EN MINAS
IIINNNGGGEEENNNIIIEEERRRIIIAAA EEENNN MMMIIINNNAAASSS
AAAPPPUUUNNNTTTEEESSS CCCUUURRRSSSOOO GGGEEEOOOEEESSSTTTAAADDDIIISSSTTTIIICCCAAA
LLLIIINNNEEEAAALLL...
PPPAAARRRTTTEEE 111
TTTEEEOOORRRIIIAAA...
1

2
REFERENCIAS BIBLIOGRAFICAS.
• SERGE SEGURET “APUNTE DE TRABAJO ENSMP”
• DAVID M. “GEOSTATISTICAL ORE RESERVE
ESTIMATION”
• XAVIER EMERY “CURSO : GEOSTADISTICA LINEAL
UNIVERSIDAD DE CHILE “
• MARCO ALFARO “CURSO DE GEOESTADISTICA UNIVERSIDAD
DE ANTOFAGASATA”
• MARCO ALFARO “ APLICACIÓN DE LA TEORIA DE VARIABLES
REGIONALIZADAS”
• CLAUDIO PACHECO “APLICACION PRACTICA DE LA
GEOESTADISTICA A UN YACIMIENTO SIMULADO”
• MARIO ROSSI “GEOESTADISTICA DE INDICADORES”
• BUSTILLO R./ LOPEZ J. “MANUAL DE EVALUACIÓN Y DISEÑO DE
EXPLOTACIONES MINERAS”
• HOWARD L. HARTMAN “SME MINING ENGINEERING HANDBOOK”
• JOSE DELGADO “APUNTES DE TRABAJO U.A”
2

3
1. INTRODUCCION
1.1 DEFINICION E HISTORIA.
La geoestadística es una disciplina relativamente nueva que se ha desarrollado y
consolidado en los últimos treinta años como una ciencia predictiva, con una sólida base
teórica y un decidido énfasis en aplicaciones a casos de la vida real, como por ejemplo a la
estimación de reservas de minerales.
La geoestadística existe únicamente como respuesta a necesidades prácticas
concretas (y esta es la base de su éxito). Con esta filosofía, la Geoestadística nació por
inspiración de un ingeniero de minas sudafricano, Daniel Krige, (Krige 1951; Krige,
1957), se desarrolló por más de quince años casi exclusivamente en el campo minero, y se
mantiene aún como una ciencia aplicada. En un esfuerzo por generar un modelo teórico,
fue la escuela matemática francesa la que consolidó sus bases en lo que hoy se conoce
como la teoría de las variables regionalizadas ( George Matheron, 1962). Esta concepción
teórica nace de la necesidad de diferenciar datos numéricos, aparentemente del mismo
tipo, pero cuya posición espacial, los hace distintos para análisis geológicos.
Esto ha originado una nueva definición de la geoestadística; la aplicación de la
teoría de las variables regionalizadas al reconocimiento y estimación de un fenómeno
natural.
1.2. CAMPO DE APLICACION
El campo de aplicación más importante de la geoestadística es, sin duda, la
minería. Sin embargo, el formalismo teórico que la sustenta es de un carácter más general,
permitiendo que esta teoría se aplique a muchos campos distintos al ámbito minero, como
son la gravimetría, hidrogeología, reconocimiento forestal, ecología, etc.
Ejemplos importantes de aplicación son:
• En la predicción de leyes de mena globales (de todo un depósito) o locales (por
ejemplo, predicciones de la ley de mena de la semana entrante o de un cierto sector
del yacimiento).
• En la aplicación de sus contenidos temáticos durante las distintas fases de la
exploración, particularmente en la decisión de dónde y cuánto muestrear
(planificación minera).
• En la determinación de las mezclas óptimas de mineral para su envío a la planta.
3

4
1.3 IMPORTANCIA DE LA GEOESTADISTICA EN LA MINERIA
La Geoestadística considera que cualquier punto de un depósito está espacialmente
relacionado con sus vecinos y cuanto más cerca mucho mayor es la correlación. Basado en
esta hipótesis, la geoestadística se convierte en una avanzada herramienta para la
estimación de reservas, resolviendo en gran medida las dudas planteadas por otras
técnicas. La base teórica de la geoestadística permite cuantificar los conceptos geológicos
de:
• Area de influencia ( rango)
• Erraticidad del depósito en estudio ( efecto pepita)
• Zonas de alta, regular y baja mineralización ( anisotropía)
• Estimación, inferencia o interpolación de valores a zonas donde no se tiene
información, minimizando el error posible.
• Error de estimación para cada punto o bloque estimado, lo cual permite conocer los
límites de confiabilidad de la estimación.( Ninguna otra técnica permite conocer estos
valores punto a punto).
• Optimización del muestreo para reducir el error de estimación, y por consiguiente
tener un gran ahorro económico para futuras campañas de muestreo en el mismo
depósito.
• Gráfica de toda esta información, lo que representa una valiosa ayuda en la toma de
decisiones.
La Geoestadística no resuelve todos los problemas en la estimación de recursos
minerales, puede considerarse como una herramienta que bien usada puede dar muy
buenos resultados. Un punto que se debe enfatizar es que cualquiera sea el método de
estimación que se use, siempre el resultado conlleva algún error y la Geoestadística no es
inmune a esta situación.
No se debe olvidar que el objetivo principal de una estimación de reservas
consiste en tratar de representar los resultados de los análisis de los datos del muestreo a
todos los puntos del depósito que interesa, y por lo tanto, obtener el dato de ley y tonelaje
que más se ajuste a la realidad.
La siguiente figura N° 1 representa en forma esquemática la función de la
Geoestadística:
4

5
GEOESTADISTICA
UNIVARIABLE
ESTACIONARIOESTACIONARIONOESTACIONARIO
GEOESTADISTICA
MULTIVARIABLE
LINEALNOLINEALLINEALLINEAL
KRIGING
ORDINARIO
KRIGING
INDICADOR
KRIGING
LOGNORMAL
KRIGING
UNIVERSAL
KRIGING
DISYUNTIVO
EXPECTACION
CONDICIONAL
COKRIGING
COKRIGING
INDICADOR
NOLINEALLINEALNOLINEAL
5

6
2. VARIABLES REGIONALIZADAS
2.1 DEFINICION
La Geoestadística establece que la distribución estadística de la diferencia en el
valor de una variable (ley) entre pares de puntos (muestras) es similar a lo largo del
yacimiento y que depende de la distancia y orientación entre los pares de puntos. Este
concepto, denominado concepto de estacionariedad, es el punto de partida de la
Geoestadística y, aunque no siempre se cumple, muy frecuentemente se asume. Así pues,
si bien la Estadística clásica considera sólo la magnitud de los datos y no toma en cuenta
ningún aspecto relacionado con la posición del dato, la Geoestadística considera no sólo el
valor del punto, sino también la posición de ese punto dentro del cuerpo mineralizado y su
relación con otras muestras. Desde un punto de vista práctico, estacionariedad implica la
decisión de trabajar con muestras localizadas en una determinada área, en forma conjunta
y derivar estadísticas e inferir parámetros de la función aleatoria de ellas. Si una función
aleatoria es estacionaria, entonces los descriptores univariables (como por ejemplo la
media, o la mediana) son independientes de las coordenadas de la muestra. De la misma
manera, parámetros como la covarianza o el correlograma son independientes de la
ubicación de cada una de las variables, y dependientes de su separación.
Una regionalización es el desplazamiento en el espacio (o en el tiempo) de un
cierto fenómeno que puede caracterizarse por magnitudes.
Una variable puede considerarse "Regionalizada" si está distribuida en el espacio y
si tiene (o muestra) algún grado de correlación espacial.
La ley de mena, espesor de una formación y la cota (altitud) de la superficie de la
tierra, son ejemplos de variables regionalizadas. En realidad, casi todas las variables que
se encuentran en las ciencias de la tierra pueden ser consideradas como variables
regionalizadas. Una variable regionalizada es una función Z(x), que representa el valor,
según su ubicación en el espacio, de una variable asociada a un fenómeno natural. Pero
esta función Z(x) no se comporta como las funciones matemáticas clásicas, debido que es
muy desordenada en su variación espacial. (ver Fig. N° 2)
FIGURA N° 2 COMPORTAMIENTO IDEAL
z(x)
x
z(x)
x
Lo ideal
matemáticamente
6

7
Una variable regionalizada se presenta bajo dos aspectos aparentemente
contradictorios:
• Un aspecto aleatorio : gran irregularidad y variaciones imprevisibles de un punto
a otro.
• Un aspecto estructural : particular a cada regionalización.
2.2 NOTACIÓN CONDENSADA.
Antes de estudiar ejemplos de variables regionalizadas se menciona que en
geoestadística se utiliza la notación condensada: un punto del espacio se representa por la
letra x; la ley en este punto se representa por Z(x). En consecuencia, se pueden anotar:
Z(x) para una variable regionalizada en un problema unidimensional. (1-D)
Z(x,y) para una variable regionalizada en un problema bidimensional. (2-D)
Z(x,y,z) para una variable regionalizada en un problema tridimensional. (3-D)
2.3 CAMPO Y SOPORTE.
Se llama campo a la zona en la cual se estudia la variable regionalizada.
El soporte es el volumen de la muestra (que puede ser el volumen que se saca para medir
ley). Se usa para indicar el tamaño, la forma y orientación de la muestra, es decir el
volumen y la geometría de la muestra. (ver Fig. N° 3)
El punto x¯es el centro de gravedad del soporte.
FIGURA N° 3 SOPORTE
Testigo
cilíndrico
x
7

8
Se usará Z(x) para representar la ley del volumen de muestra localizado en el punto x.
Nota: en el estudio de una variable regionalizada no es conveniente mezclar soportes
diferentes.
2.4 OBJETIVOS DE LA TEORÍA.
La teoría de las variables regionalizadas se propone dos objetivos principales:
A. En el plano teórico, expresar las características estructurales de una variable
regionalizada mediante una forma matemática adecuada.
B. En el plano práctico, resolver el problema de la estimación de una variable
regionalizada, a partir de un muestreo fragmentario.
A. Características Estructurales
Se entiende por características estructurales:
A.1. Continuidad de las leyes: Diferenciar y caracterizar la regularidad de un
yacimiento en casos tales como en la Fig. N° 4
FIGURA N° 4 CONTINUIDAD DE LAS LEYES
Yacimiento 1
Z (x)1
x
Z (x)2
x
Yacimiento 2
8

9
A.2. Anisotropía: Detectar direcciones privilegiadas de la mineralización (ver Fig. N°5)
B. Problema de Estimación
Se entiende por resolver el problema de estimación, el determinar de manera
satisfactoria una estimación de una variable regionalizada a partir de un conjunto de
muestras, asignando errores a las estimaciones (globales y locales).
(Ec. 1)
Los dos objetivos están relacionados: el error de estimación depende de las
características estructurales (continuidad, anisotropías) y se tendrá un error mayor si la
variable regionalizada es más irregular y discontinua en su variación espacial.
Para alcanzar estos objetivos es necesario introducir un modelo matemático.
3.2.1. MODELO MATEMATICO
Para alcanzar los objetivos propuestos por la geoestadística es necesario disponer
de un modelo matemático. La geoestadística utiliza una cierta interpretación
probabilística de la variable regionalizada, mediante el modelo de las funciones aleatorias.
En estadística clásica, se consideran los valores muestreados como realizaciones
independientes de una misma variable aleatoria, es decir, que se suponen independientes
unas de otras, y obedecen a la misma ley de probabilidad. Se busca entonces modelar la
distribución de probabilidad de los valores y estimar sus parámetros. Sin embargo, cuando
Anisotropía
Hay una dirección
privilegiada de la veta
FIGURA N° 5 ANISOTROPIA
9

10
los datos están ubicados en el espacio geográfico, las hipótesis de la estadística clásica son
raramente aceptables. Por lo tanto se debe definir el concepto de variable regionalizada,
que se trata simplemente de una función definida en todo punto del espacio geográfico y
que representa numéricamente el fenómeno regionalizado estudiado.
Una variable regionalizada posee las siguientes características, contradictorias en
apariencia:
1) localmente, es muy irregular, o errática, y requiere un modelamiento probabilístico;
2) globalmente, presenta cierta estructura en el espacio (zonas de altos valores o “ricas” /
zonas “pobres”), lo que sugiere una cierta interpretación funcional.
Los modelos geoestadísticos consideran el valor z(x) de la variable regionalizada en un
punto x del campo D como una realización de una variable aleatoria Z(x). Las variables
aleatorias Z(x) así definidas no son independientes. Por el contrario, están correlacionadas,
y son precisamente sus correlaciones las que reflejarán la “estructura” del fenómeno
regionalizado, y en especial su grado de continuidad y regularidad espacial. Así en
globallocal
zona
rica
zona
pobre
0 20 40
2
4
6
8
10
12
14
z(x)
0 200 400
0
5
10
15
20
25
30
z(x)
FIGURA N°6: Aspectos local y global de una variable regionalizada
10

11
geoestadística probabilística, se interpreta la variable regionalizada como una
realización de una función aleatoria.
Llamamos funciones aleatorias a un grupo de variables aleatorias distribuidas en el
espacio, cada una identificada por su correspondiente coordenada espacial, y cuya
dependencia entre sí está gobernada por un mecanismo probabilistico. Es decir, una
función aleatoria es una función Z(x) que asigna a cada punto x del espacio un valor que
depende del azar. Al hacer un experimento sobre una función aleatoria se obtiene un a
función ordinaria z(x) llamada realización de la función aleatoria Z(x).
La hipótesis constitutiva de la geoestadística consiste en afirmar que la variable
regionalizada en estudio es la realización de un acierta función aleatoria. Lo anterior
equivale a decir que las leyes de nuestro yacimiento se generaron a partir de un proceso o
experimento muy complejo.
Este enfoque permite tomar en cuenta los aspectos erráticos y estructurados de la
variable regionalizada:
1) localmente, en el punto x, Z(x) es una variable aleatoria (de donde proviene el aspecto
errático);
2) para todo conjunto de puntos x1, x2,… xk, las variables aleatorias Z(x1), Z(x2),… Z(xk)
no son, en general, independientes, sino que están ligadas por unas correlaciones que
cuantifican la “semejanza” entre los valores que toman (de donde proviene el aspecto
estructurado).
En geoestadística lineal, se usan sólo los dos primeros momentos (Los momentos
de una función aleatoria son parámetros descriptivos de su ley espacial, bastantes simples,
como para ser, a menudo, fáciles de calcular.) de la función aleatoria. Entregan una
descripción elemental de la ley espacial, y son suficientes para resolver la mayor parte de
los problemas encontrados en la práctica.
3.2.2. CONTINUIDAD ESPACIAL.
En geoestadística se entiende por medida de la continuidad espacial al análisis de
covariogramas, variogramas y correlogramas.
Se presentan a continuación algunas funciones básicas utilizadas para describir la
medida de la continuidad espacial entre dos variables:
11

12
3.2.1. Covariograma
(Ec. 2)
Donde N(h) es el número de parejas (z(xi), z(xi + h)) de datos a una distancia h dada. m-h
es la media de los valores izquierdos (si existen) de las parejas de datos a distancia h,
definida por:
(Ec.3)
Análogamente,
(Ec. 4)
Define la media de los valores derechos (si existen) de las parejas de datos a distancia h.
3.2.2. Correlograma
(Ec. 5)
donde C(h) es la covarianza, s-h y s+h son las varianzas correspondientes a cada lado de
los pares a distancia h.
12

13
3.2.3. Variograma
Es una representación gráfica de la interdependencia direccional de las leyes de las
muestras.
(Ec. 8)
3.3. RELACIONES ENTRE LAS FUNCIONES DE MEDIDA DE LA
CONTINUIDAD ESPACIAL
Las relaciones entre las funciones con que se caracteriza a la continuidad espacial
se cumple si los datos son considerados como estacionarios. El carácter estacionario
implica la homogeneidad de Z(x) en el espacio y significa que el fenómeno representado
Z(x) se repite indefinidamente en el espacio.
Una función aleatoria es estacionaria de segundo orden si la variable aleatoria z(x0)
admite una esperanza matemática independiente del punto de apoyo x0:
m = E { Z (x)} (Ec. 9)
(Ec. 6)
(Ec. 7)
13

14
y si para todo vector h la covarianza está dada por:
C(h) = E { Z(x0) Z(x0+h) } (Ec. 10)
existe y es independiente de x0. La covarianza da una visión elemental del “acoplamiento”
que existe entre Z(x1) y Z(x2). Es una forma bilineal, donde la varianza es la forma
cuadrática asociada. Pero esta hipótesis supone la existencia de una varianza a priori finita
C(o), es decir
C(0) = E { [Z(x)]2
} (Ec.11)
que es la varianza de la variable aleatoria Z(x0).
Es así como los autores de Africa del Sur (D.G. Krige..) a partir del enorme
archivo de datos del Yacimiento de Oro de Rand, calcularon la varianza de estas muestras
en paneles más y más grandes, finalmente en todo el conjunto del Yacimiento de Rand se
pudo concluir con certeza que no existe en este caso una varianza a priori finita.
Luego se debió reemplazar la hipótesis estacionaria de segundo orden por una
hipótesis más débil, pero de significación análoga:
Hipótesis Intrínseca:
Aún en el caso en que la varianza a priori C(o) no existe (es infinita) puede suceder
que los incrementos: Z (x0+h) - Z(x0) tengan una varianza finita. Diremos entonces que
la función aleatoria Z(x) verifica la hipótesis intrínseca si, para todo vector h, el
incremento Z (x0+h) - Z(x0) verifica las hipótesis:
Hipótesis Intrínseca
(Ec. 12)
E [ ] = m (h)Z Z(x+h) - (x)
14

15
Luego la función g (h) :
(Ec. 13)
Se llama semivariograma o función intrínseca. Una función aleatoria que verifica
la hipótesis intrínseca constituye lo que se llama esquema intrínseco, caracterizado por su
semivariograma.
Si Z(x) verifica la hipótesis estacionaria de segundo orden, el variograma y
covariograma estarán relacionados:
La relación entre el semivariograma y el covariograma cuando las condiciones de
estacionaridad de segundo orden se cumplen está dada por:
(Ec. 15)
donde s2 es la varianza de los datos, C(h) es el covariograma.
La relación entre el semivariograma y el correlograma queda dada por:
E [ - ]z(x+h) z(x)
E {[ ] }2
z(x+h) - z(x)
2γ (h)
= E [ z(x+h)] - E[ z(x) ] = 0
= E { [[ z(x+h)] + [ z(x) ] - 2 z(x+h) z(x)] }2 2
γ (h) = [ - (h)]Cσ
2
= E{ [ z(x) ] } - 2EE{ [z(x+h) ] } + [2 2
z(x+h) z(x)]
= 2 (0) - 2 (h),C C luego se tiene
γ (h) = σ2
- (h)C
(Ec. 14)
15

16
(Ec. 16)
γ (h) = σ ρ2
[ 1- (h)]
γ( )h
Co
γ( )h
h
σ
2
Co
γ( )h En general se cumple: σ =/ 0
2
ρ(0) =1 =/ 0
γ(0) = 0
γ( )h
h
C(h)= σ −γ( )
2
h
σ2
FIGURA N° 3.8
FIGURA N° 3.9
16

17
4. VARIOGRAMA
4.1 DEFINICION
Puesto que la Estadística clásica considera las muestras como aleatorias y
completamente independientes entre sí, mientras que la Geoestadística asume una
correlación entre ellas, una forma de expresar dicha correlación es a través de una función
denominada variograma o semivariograma
El Variograma es considerado un elemento esencial en el análisis espacial de datos.
Básicamente, el Variograma es una herramienta matemática que intenta capturar el nivel
de continuidad de una función aleatoria. David (1978) define el Variograma como una
función que mide el grado de similitud (correlación) o dependencia entre dos pares de
muestras separadas a una distancia h, en una dirección establecida. (ver Fig. N°10)
FIGURA N° 10 VARIOGRAMA
Esta función define, por tanto, la correlación espacial entre los valores
muestreados. El variograma o semivariograma se obtiene calculando, para cada distancia
de separación entre las muestras (lag) en una determinada dirección, la diferencia al
cuadrado de los valores de dichas muestras. La definición teórica de la función
semivariograma g (h) es:
(Ec. 17)
x
x+ h
γ (h) = (1/2) E [ z(x+h) - z(x)]
2
17

18
Y en la práctica se usa el algoritmo siguiente:
(Ec. 18)
Propiedades del Variograma:
• El variograma es simétrico: (h) (h).
• Se anula en el origen: (0) 0.
• Es positivo o nulo: (h) ≥ 0.
La gran ventaja del variograma es que incorpora parámetros estructurales tales como:
• Continuidad o falta de continuidad de la mineralización se refleja en la razón del
incremento del g (h) para valores pequeños de h.
• Zona de influencia conocido como alcance y que representa la distancia en la cual
influye el valor de una muestra sobre las muestras vecinas.
• Anisotropía es una medida de los cambios laterales en la mineralización.
• Correlacion es conocido como meseta y representada en el gráfico por la altura
máxima que alcanza. También es la variación que existe entre las muestras separadas a
cierta distancia dentro de un depósito mineral.
La velocidad del incremento de g(h) con el lag es un reflejo de la velocidad a la cual la
influencia de una muestra disminuye con la distancia, y nos da una definición adecuada de
la denominada zona de influencia. La distancia en la que g(h) se hace constante
corresponde al punto en el que la covarianza cov(h) entre muestras adyacentes disminuye
hasta cero. Esta distancia define el límite de la zona de influencia de una muestra.
γ (h) = (1/2) Promedio
{(diferencias) de leyes
en datos que están a
la distancia h
2
}
18

19
4.2. CONSTRUCCION DE UN VARIOGRAMA
Antes de construir el variograma asociado a una variable regionalizada es
conveniente efectuar un análisis de los datos. Entre otras cosas hay que examinar:
• Soporte de la variable: ¿ está bien definido?
• Método de muestreo.
• Implantación y orientación de sondeos.
• Técnicas de análisis: ¿existen errores de cuarteo, de análisis?
• Crítica general del reconocimiento. ¿es sistemático, existen sesgos?
• Homogeneidad: no mezclar zonas heterogéneas.
La siguiente figura N° 11 muestra el papel del variograma como herramienta en el
análisis espacial de datos.
En la práctica, la construcción de un Variograma se puede lograr en una, dos o tres
dimensiones (en otras palabras, en una línea, una superficie o un volumen).
19

20
TIPOS
ESTRUCTURASANISOTROPIAS
SOPORTECORREGIONALIZACION
VARIOGRAMA
SIMPLE
VARIOGRAMA
INDICADOR
VARIOGRAMA
RESIDUAL
VARIOGRAMA
CRUZADO
VARIOGRAMA
RELATIVO
ZONADEINFLUENCIA
CONTINUIDADCERCA
DELORIGEN
MESETA
RANGO
a1
a2
RANGOS
a1
a2
ELIPTICOESTRATIFICADO
HOR.
VER.
PUNTO
VARIOGRAMA
MUESTRAS
REGULARCONTINUOSEFECTO
PEPITA
ALEATORIO
VARIABLE1
ANALISIS
GEOESTADISTICO
UNIVARIABLE
ANALISIS
GEOESTADISTICO
MULTIVARIABLE
VARIABLE2
VARIOGRAMA
CRUZADO
{
{
20

21
4.2.1.1. COMPORTAMIENTO DEL VARIOGRAMA PARA DISTANCIAS
PEQUEÑAS
Se estudiará el comportamiento de la función g(h), para distancias pequeñas.
Se analizará cuatro casos en la siguiente figura N° 12
FIGURA N° 12 VARIOGRAMAS PARA DISTANCIAS PEQUEÑAS
• Caso 1: Leyes muy regulares y continuas. Z(x) es una función muy regular, su
interpretación en un variograma es en forma parabólica en el origen.
• Caso 2: Leyes un poco irregulares. En este caso la interpretación a través un
variograma genera un comportamiento lineal en el origen.
Ley
0 x
x x+h
γ( )h
0 h
Ley
0 x
γ( )h
→
0 h
→
21

22
Caso 3: Leyes con microvariaciones. Su interpretación a través de un variograma
genera un efecto pepita, es decir existe una discontinuidad aparente.
• Caso 4: Leyes con Irregularidad total. (sin ninguna relación)
γ( )h
→
Ley
I I
0 x 0 d h
→
γ( )h
→
Ley
I I
0 x 0 h
→
Co
22

23
4.2.1.2. COMPORTAMIENTO DEL VARIOGRAMA PARA DISTANCIAS
GRANDES
Se estudiará el comportamiento de la función g(h), para distancias grandes. Se
analizará tres casos en la Fig. N° 13
FIGURA N° 13 VARIOGRAMAS PARA DISTANCIAS GRANDES
• Caso 1: Leyes con crecimiento (decrecimiento) progresivo.
• Caso 2: Leyes con pseudo-periodicidades . En el caso que exista periodicidad no se
observa una tendencia clara del variograma a escala de observación que se tenga.
Normalmente entre lo que podría llamarse un ciclo, se observa la formación de una
dispersión que frecuentemente se conoce como efecto hoyo.
Ley
0 x 0
γ( )h
→
h
→
Ley
0 x 0
γ( )h
→
h
→
23

24
• Caso 3: Fenómeno estacionario (sin pseudo periodicidades y tendencias).
4.2.2. CONSTRUCCION DE UN VARIOGRAMA PARA UNA MALLA REGULAR
BIDIMENSIONAL.
Se usará una malla regular (ver fig. N° 14) para una mejor visión gráfica.
FIGURA N° 14 MALLA REGULAR BIDIMENSIONAL.
Se sabe que el semivariograma depende de “h” que ahora toma un carácter
vectorial en dos dimensiones. (ver fig. N° 15)
Ley
0 x 0 a
γ( )h
→
h
→
θ
24

25
FIGURA N° 15 DIAGRAMA VECTORIAL
En este caso h es un vector
h = (hx, hy) coordenadas cartesianas
h = (h,θ) coordenadas polares
La práctica demuestra que para estudiar la estructura basta con calcular el variograma g
(h) en cuatro direcciones. Por ejemplo: q = 0°, q = 45°, q = 90°, y q = 135°.
4.2.3 CONSTRUCCION DE UN VARIOGRAMA PARA UNA MALLA IRREGULAR
BIDIMENSIONAL.
En la figura N° 16 puede verse la localización irregular de los datos.
FIGURA N° 16 MALLA IRREGULAR BIDIMENSIONAL.
hx
hyh
θ
25

26
Para calcular el variograma a una distancia h=(hx, hy) lo más probable es que no se
encuentre ningún o muy pocos pares de datos que estén exactamente a esa distancia. El
método de los sectores puede solucionar este problema.
• Método de los sectores.
Este método se basa en la aproximación siguiente, determinada por los elementos
de la ilustración que se muestra en la figura N° 17: Dos puntos se considerarán a la
distancia h si una vez fijado el primero, el segundo cae en la zona achurada de la figura.
FIGURA N° 17 FIGURA DE BUSQUEDA
A
h = h = h1 2
B
26

27
En ella se ha procedido como sigue:
1. Se fija un punto A en uno de los datos de la malla irregular, respecto del cual se va
identificar la distancia h.
2. Con vértice en A, se definen los parámetros de construcción de la figura de
búsqueda (sector achurado) en donde se identifica:
• Un ancho de Banda (máximum bandwidth)
• Un ángulo de tolerancia ( q )
• Una tolerancia en distancia (e).
3. Una vez establecido el sector achurado o lag, se determina la pareja asociada a AB,
donde B es un dato del lag a la distancia h de A.
4. Al pasar por cada uno de los datos se realiza el procedimiento anterior para
determinar el número de parejas asociados a distintas distancias h (identificados
por los lag en la fig. N° 3.18).
FIGURA N° 3.18 FIGURA DE BUSQUEDA A DISTINTOS LAG
Nota: Estas figuras de búsquedas se realizan en las direcciones principales de estudio.
Dirección
Maximun
bandwidth
lag 0
lag 1
lag 2
lag 3
lag 4
lag
Tolerancia
lag de
espaciamiento
Y
X
Tolerancia
Angular
27

28
Este método tiene problemas, ya que pueden caer más de un dato en la zona achurada; en
este caso se considera la media de los datos.
4.2.4 ANÁLISIS DE LAS CARACTERÍSTICAS DEL VARIOGRAMA.
El Variograma es un gráfico en dos dimensiones donde el eje horizontal representa
la distancia entre pares de muestras y el eje vertical representa el variograma de los datos
analizados en una dirección dada, como se observa en la figura N° 19:
FIGURA N° 19 ELEMENTOS DEL VARIOGRAMA
• El rango o alcance es la distancia h a la cual el variograma alcanza la meseta.
• El efecto pepita es identificado por Co , valor determinado por la proyección de la
trayectoria del variograma, hasta cortar el eje vertical. Si Co > 0 entonces, existe una
concentración de microvariaciones y/o a errores en la manipulación, preparación o
análisis químico de la muestra.
• El efecto pepita incrementa la varianza total del variograma.
• El alcance “a” proporciona una medida de la zona de relación entre muestras (ver Fig.
N° 20) a distancia h £ a (correlacionadas), donde:
• Una distancia mayor al rango o alcance indica que las muestras se
consideran independientes.
• Una distancia menor al rango o alcance indica muestras correlacionadas
entre sí.
γ( )h
0
h
{
MESETA = CO
CO
C
a
28

29
FIGURA N° 20 DIAGRAMA DE RELACION ENTRE MUESTRAS
4.3 AJUSTE DEL VARIOGRAMA
Como se verá posteriormente, la estimación de la variable en un punto a través del
Krigeage necesita de la utilización del semivariograma, pero no en la forma del
semivariograma experimental, pues éste posee numerosas zonas donde no existen valores
concretos (únicamente existen valores definidos en aquellos lugares donde se ha realizado
el muestreo). Por tanto, puede resultar necesario definir el valor de la variable en puntos
donde el semivariograma experimental no ofrece información suficiente. Para ello, es
necesario construir un modelo que sí nos permita obtener dicha información. Ahora bien,
la pregunta que surge es: ¿qué modelos pueden utilizarse?. A continuación se va a intentar
resolver esta pregunta de la forma más sencilla posible.
La información más interesante que debería considerarse a la hora de intentar
resolver el problema de la estimación de una variable es la descripción de cómo se ha
producido el fenómeno. En determinadas situaciones, los procesos físicos o químicos que
generan el conjunto de datos pueden ser conocidos con suficiente detalle como para
avanzar una descripción completa del perfil a partir de unos únicos valores. En dichas
situaciones, aplicar modelos determinísticos sería lo más apropiado. Sin embargo,
desgraciadamente son pocos los procesos naturales cuyas pautas de comportamiento son
tan bien conocidas como para poder utilizar este tipo de modelos. La mayor parte de estos
procesos son, en realidad, el resultado final de una combinación de variables cuyas
complejas interacciones impiden describir el fenómeno cuantitativamente.
En las Ciencias de la Tierra es necesario admitir la existencia de incertidumbre en el
comportamiento del fenómeno entre los puntos muestreados, por lo que es imprescindible
acudir a los modelos de funciones aleatorias, que permiten resolver esta problemática
planteada. Por esta razón, los estudios de estimación geoestadística se basan en modelos
probabilísticos que reconocen estas incertidumbres. En los modelos probabilísticos, el
conjunto de datos se muestra como el resultado de la actuación de procesos aleatorios.
Independencia
x -a0
a a
x0 x +a0
IndependenciaRelación
Datos
29

30
Una variable aleatoria es aquella cuyos valores se generan aleatoriamente de
acuerdo con un mecanismo probabilístico. El ejemplo clásico de este tipo de variables
aleatorias sería el resultado de tirar un dado, cuyas realizaciones se reparten
aleatoriamente entre las seis posibilidades existentes en el dado. De igual forma, se puede
definir una función aleatoria como un conjunto de variables aleatorias que tienen alguna
localización espacial y cuya dependencia, una de otra, viene determinada por algún
mecanismo probabilístico. Este tipo de funciones aleatorias son las que utiliza la
Geoestadística.
Aunque el ajuste de un modelo a un semivariograma experimental es la forma más
común de aproximación al esquema de continuidad espacial, no es la única ni
necesariamente la mejor. Existen numerosas situaciones en las que la selección del
modelo adecuado se debe basar principalmente en aproximaciones cualitativas. La
experiencia con conjuntos de datos semejantes puede constituir una guía más óptima que
el simple esquema mostrado por unas pocas y solitarias muestras. Más aún, la posible
existencia de un semivariograma aparentemente sin posibilidad de modelización no debe
obviar este proceso, pues, muchas veces, problemas como un número insuficiente de
muestras, errores en el muestreo, valores erráticos, etc., pueden enmascarar el esquema
real de continuidad espacial. En resumen, la selección del modelo a aplicar es un
cuidadoso proceso en el que se deben considerar todos los aspectos involucrados.
Tal como se ha indicado, existe un grupo de modelos que constituyen la base más
frecuente a la hora de optar por el modelo más adecuado al semivariograma experimental,
todos ellos cumpliendo la condición matemática anteriormente citada. Aunque este
cumplimiento pueda parecer, en principio, una restricción, no lo es tanto, pues la
combinación de los diferentes modelos genera otros que también cumplen dicha
condición, por lo que el abanico final es lo suficientemente amplio como para satisfacer
las necesidades requeridas. En otras palabras, cualquier modelo, o combinación de
modelos, de los que a continuación se van a citar, permite ajustar todos los
semivariogramas que puedan aparecer en el estudio de las variables de carácter minero.
El ajuste del variograma teórico debe representar fielmente los aspectos que
considera importantes el variograma experimental (ver Fig. 21). Es el variograma teórico
el que será utilizado en los cálculos posteriores.
Se distinguen dos tipos de variogramas:
• Variograma Experimental : Calculado a partir de los datos.
• Variograma Teórico : Ecuación que se ajusta al variograma experimental
30

31
FIGURA N° 21 GRAFICA DE AJUSTE DEL VARIOGRAMA
El variograma teórico debe respetar al variograma experimental, sobre todo en los
primeros puntos, ya que son los más confiables.
Para tener un buen ajuste es necesario considerar una cierta vecindad restringida de
manera de no considerar demasiadas muestras para estimar la ley del bloque.
Los modelos a considerar se pueden agrupar en dos grandes categorías: (a) los que
alcanzan una meseta (modelos de transición) y (b) los que no alcanzan una meseta.
En el primer grupo se incluyen aquellos modelos en los que la curva asciende de
forma continuada hasta alcanzar un nivel, denominado meseta. La distancia a la que
alcanzan la meseta se denomina alcance o rango. Entre estos modelos, los más
característicos son el exponencíal y el esférico o Matheron. En el segundo grupo están
los que van incrementándose a medida que la distancia aumenta, sin llegar a alcanzar una
meseta. Los más representativos son el lineal y el de Wijsian. A continuación se van a
describir todos ellos, centrándose, especialmente, en el denominado esférico o Matheron,
que es el que presenta un mayor número de aplicaciones en minería.
Previamente hay que hacer constar que, teóricamente, el valor del semivariograma
para una distancia cero debería ser cero. Sin embargo, muchas veces esto no sucede,
generando lo que se denomina efecto pepita (Co) (el nombre hace mención a la aparición,
mas o menos errática, de pepitas de oro en algunos yacimientos auríferos). Sus causas
pueden ser muy variadas: errores de muestreo, fluctuaciones de la variable a una escala
menor que la de observación, etc. Dado que su presencia es bastante común, hay que
γ( )h
⎪h⎪
Variograma experimental
Variograma teórico
31

32
acostumbrarse a trabajar con ella, lo que no necesariamente significa un menoscabo en la
utilidad y exactitud de la técnica de estimación.
1) Modelo exponencial
Este modelo va ascendiendo lentamente hasta alcanzar la meseta a un valor
constante. Existen dos posibles esquemas: Formery y Gaussiano. El primero tiene la
expresión:
g(h) = C [1 - exp(-[h/a])] + Co
Done C es el valor comprendido entre el efecto pepita (Co) y la meseta, h la
distancia y a representa el alcance o rango. En este esquema la tangente en el origen
intercepta la meseta a un valor de a/3. Por su parte, el esquema Gaussiano posee la
siguiente expresión:
g(h) = C [1 - exp(-[h2
/a2
])] + Co
en este caso, la tangente en el origen intercepta la meseta a un valor de a/√3.
2) Modelo esférico o Matheron
El modelo esférico o Matheron es el que mejor se suele ajustar cuando se trata de
variables mineras ( ley o espesor). El modelo esférico presenta una curva del
semivariograma que aumenta rápidamente para bajos valores del lag para,
posteriormente, ascender más lentamente hasta alcanzar una zona plana a valores del lag
altos. Una tangente a la curva, dibujada a partir de los dos o tres primeros puntos, define
un par de valores en el eje X (g(h)) que se denominan Co y C. Esta tangente, a su vez,
intersecta la prolongación de la zona plana a 2a/√3, siendo a el punto, en el eje Y (lags),
donde el semivariograma alcanza la zona plana. La distancia entre la curva y la zona
plana para lags inferiores a "a" representa la covarianza entre las muestras. Más allá de
a, la covarianza es cero y, por tanto, no hay relación entre las muestras tomadas a esas
distancias.
g(h) = Co + C [1.5(h/a) - 0,5(h/a)3
] para h < a
g(h) = Co + C para h > a
Donde Co es el efecto pepita, Co +C es el valor de la meseta, a es el alcance o
rango y h es el valor del correspondiente lag. Co +C viene a representar el equivalente
32

33
geoestadístico de la varianza del conjunto de datos. Si el semivariograma muestra
fluctuaciones aleatorias alrededor de una línea horizontal, entonces se tiene lo que se
denomina efecto pepita puro, siendo mejor, en este caso, llevar a cabo la evaluación del
yacimiento por cualquiera de los métodos clásicos comentados anteriormente. No
obstante, la presencia del efecto pepita puro no implica necesariamente una ausencia de
continuidad en la estructura del semivariograma sino que puede ser debido, por ejemplo, a
una red de muestreo con distancias muy grandes entre muestras.
3) Modelo lineal
Este modelo se presenta cuando, al representar V*(h) frente a los lags, se obtiene una línea
recta. El modelo presenta la ecuación:
g(h) = p.h + k
donde p es la pendiente de la recta, h el lag y k la intersección en el eje X (g(h))
Este modelo suele estar presente en algunos yacimientos de hierro (Annels, 1991).
4) Modelo de Wijsían
En este modelo, al igual que en el anterior, g(h) se incrementa más allá del valor de
la varianza de los datos. En una primera observación, parece ser semejante al modelo
lineal, pero si se representan los valores de g(h) frente al logaritmo de h, entonces se
obtiene una línea recta. Tiene la expresión:
g(h) = 3 α [Ln(h/L) +3/2]
Donde α es el coeficiente de dispersión absoluta, una medida de la variación
espacial, y L se define como el espesor equivalente. Ambos coeficientes pueden
determinarse calculando los valores de g(h) para dos lags, con lo que se obtiene dos
ecuaciones con dos incognitas. Este tipo de modelo tiene una aplicación más restringida
aún que el lineal, estando presente únicamente en algunos yacimientos hidrotermales,
principalmente de estaño, y utilizando como variable el espesor del cuerpo mineralizado.
Algunas particularidades respecto a los modelos de variogramas
Existen situaciones en las que, si bien no es posible el ajuste inmediato de un tipo concreto
de modelo, no hay razones para rechazar la posibilidad de buscar una continuidad
espacial. Entre las muchas posibilidades existentes, Anneis (1991) pone de manifiesto
algunas muy características, como son:
33

34
a) Semivariogramas con tendencias.
b) Semivariogramas con efecto agujero.
c) Semivariogramas compuestos.
d) Semivariogramas con estructuras anidadas.
e) Anisotropia.
a) SEMIVARÍOGRAMAS CON TENDENCIAS
Una asunción que se hace en la Geoestadística es que no existen tendencias dentro del
yacimiento que puedan causar una ruptura en el concepto de estacionariedad. La ruptura
(o cambio en la tendencia de la meseta), se produce en una distancia claramente superior
al alcance, por lo que no tiene una mayor incidencia en la estimación local de los bloques
definidos para el yacimiento, pues las dimensiones del área de búsqueda (alcance) son
menores que la distancia representada por el punto donde se produce la ruptura. Cuando
este tipo de comportamientos dominan el semivariograma, es decir, la ruptura se produce a
distancias próximas al alcance, con lo que se rompe el concepto de estacionariedad, es
necesario utilizar una técnica que se denomina Krigeage universal (Journel y Huijbregts,
1978), en lugar del Krigeage ordinario que se aplica en las situaciones de estacionariedad.
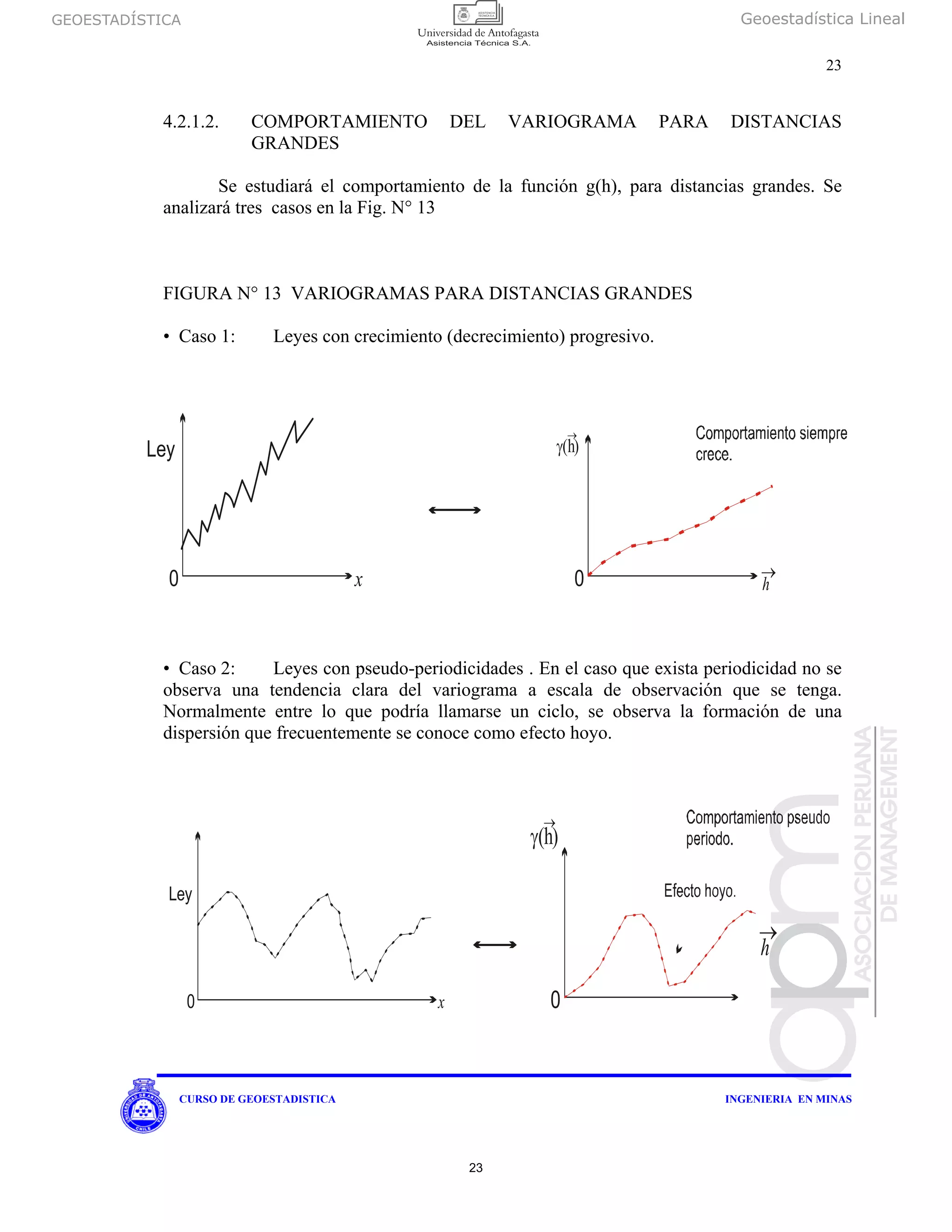
b) SEMIVARIOGRAMAS CON EFECTO AGUJERO O EFECTO HOYO
Este efecto puede reconocerse cuando alternan áreas con alta ley y áreas con baja ley. El
resultado es una pseudoperiodicidad reflejada en una oscilación del semivariograma
alrededor de una aparente-meseta.
c) SEMÍVARIOGRAMAS COMPUESTOS
Cuando la prolongación de la línea que une los dos o tres primeros puntos del
semivariograma corta la meseta a una distancia mucho menor que la correspondiente al
alcance general del semivariograma, es muy probable que la situación corresponda a una
mezcla de dos semivariogramas esféricos.
El modelo compuesto tendría, pues, la siguiente forma:
g(h) = Co + C1 [3h/2a1 - (h/ a1)3
/2] + C2 [3h/2 a2 - (h/a2)3
/2]
Así es posible calcular el valor de g(h) para cualquier distancia, teniendo en cuenta
las tres partes que definen el semivariograma.
34

35
Este tipo de estructuras pueden ser causadas, por ejemplo, por la presencia de
zonas mineralizadas más ricas dentro de una matriz de mineralización dispersa. También
son comunes en yacimientos aluviales de oro, reflejando el alcance más corto los canales
individuales y el más largo la anchura total de la zona de interés económico.
e) ESTRUCTURAS ANIDADAS
En aplicaciones reales es común encontrar que los variogramas experimentales se
pueden modelar con más de una estructura teórica. Por ejemplo, el variograma típico no
parte de cero, sino que muestra una discontinuidad en el origen (efecto pepita). Por ello, la
primera estructura del modelo considerará un valor en el origen, Co . Además, el
variograma suele mostrar distintos tipos de correlación espacial a distintas distancias.
Una estructura de rango largo puede estar sobreimpuesta con una estructura de
rango corto. El uso de modelos anidados provee suficiente flexibilidad para tomar en
cuenta ambas estructuras. Es de tener en cuenta que la sobre-sofisticación de por sí
generalmente no produce beneficios. Cada una de las estructuras modeladas debe ser
explicada por la geología del depósito o los fenómenos físicos involucrados. Por ejemplo,
cierto mineral puede presentar regionalizaciones de distinto rango, correspondiente a
distintas etapas en la mineralización. Tal caso podría ser modelado con tal vez el mismo
tipo de función (esférica, por ejemplo), de distintos rangos.
d) MODELAMIENTO DE LA ANISOTROPÍA
El comportamiento de los variogramas experimentales en distintas
direcciones puede ser la clave para entender y caracterizar la variable regionalizada. Hay
dos modelos básicos de anisotropía:
• Anisotropía Geométrica.
• Anisotropía Zonal
1. ANISOTROPÍA GEOMETRICA
Si los variogramas en las direcciones principales presentan un mismo valor
de meseta, pero alcances distintos para diferentes direcciones como lo muestra la figura
N° 22, hablamos entonces de Anisotropía Geométrica:
35

36
FIGURA N° 22 ANISOTROPÍA GEOMETRICA
Estos tipos de variograma se pueden reducir a un variograma isótropo mediante
una transformación lineal de las coordenadas.
Luego la elipse de anisotropía geométrica (rosa de alcances) queda gráficamente en la Fig.
23 como:
FIGURA N° 23 ELIPSE DE ANISOTROPÍA GEOMETRICA
Donde los alcances a1 y a2 corresponden a los valores de las longitudes de los semiejes de
la elipse.En el caso isótropo los alcances son iguales y, por tanto, la figura se convierte en
un circulo.
Sea el factor de anisotropía k=( a1/a2) > 1, donde k es la razón del alcance mayor
al menor.
o
c
dir 2
dir 1
a2 a1
γ( )h
⎪h⎪
x’
xx
ϕ
yy’
a2
a1
36

37
Las fórmulas de transformación de coordenadas nos muestran que:
(Ec. 20)
Donde ϕ es el ángulo formado entre el eje x y el eje x’ de la elipse. g1 es el
variograma de la dirección 1.
2. ANISOTROPÍA ZONAL
Se habla de Anisotropía Zonal cuando los variogramas de la zona en estudio
presentan distinto valor de meseta y distinto alcance para diferentes direcciones, como lo
muestra la Fig. N° 24
FIGURA N° 24 ANISOTROPÍA ZONAL
o
c1
c2
dir 2
dir 1
a2 a1
γ( )h
→
γ( )h1
→
γ( )h2
→
⎪h⎪
→
37

38
5. VALIDACION CRUZADA
5.1. DEFINICION
Es una técnica simple, cuyo objetivo consiste en determinar el modelo del
variograma obtenido con los datos muestrales que mejor los representa. Se trata de elegir
el mejor entre dos o más modelos alternativos disponibles y así usar con mayor
certidumbre dicho modelo en un krigeage.
La idea es estimar Zv, en cada ubicación donde exista una muestra en un bloque o
zona V (ver Fig. N° 25). Ignorando el valor de la muestra existente en ese punto, se estima
Zv a partir de las muestras colindantes dentro de la zona de interés, utilizando el modelo
del variograma y el krigeage. Una vez estimada esa muestra, la siguiente se estima
restituyendo el valor original anterior. Se repite el proceso tantas veces como muestras
hayan. Al final se conoce en cada punto de la zona de interés, un valor observado y un
valor estimado, pudiéndose establecer, a continuación, una relación entre ambos tipos de
valores, lo que da una medida de los errores cometidos. Como el Krigeage utiliza el
semivariograma, variando los valores de éste se podrá buscar la opción que genere una
menor diferencia entre los valores estimados y los reales. Este proceso iterativo permitirá
definir qué parámetros del semivariograma (los citados efecto pepita, meseta y alcance)
son los más adecuados para la óptima modelización. La mejor situación sería que todos los
puntos estuviesen situados en la bisectriz del cuadrante, lo que indicaría que el valor real
(Z) y el estimado (Z’) son semejantes. Todo lo que se separe de dicha bisectriz indica
error en la estimación.
Algunos especialistas han cuestionado la validez y utilidad del método, principalmente
porque no es suficientemente sensitivo como para detectar ventajas menores de un modelo
de variograma comparado con otro. (clark, 1986, Davis, 1987, Isaaks and Srivastava,
1989). Además, el análisis se realiza utilizando las muestras, lo que no permite obtener
una conclusión definitiva acerca de toda el área A. En particular, si las muestras no son
representativas del área, re-estimar con buena precisión estas muestras no implica que el
modelo de variograma permita una buena estimación del resto del depósito.
Sin embargo, la técnica es útil como una indicación general de las bondades (o los
posibles problemas) asociados con el modelo de variograma escogido. Además, los datos
estadísticos recogidos permiten entender mejor los resultados del estudio geoestadístico, y
por ello se debe poner a la validación cruzada como una técnica más del análisis
exploratorio de los datos. También permite detectar los problemas mas serios durante el
proceso de estimación, como son problemas computacionales, errores groseros, etc. En
general, la validación cruzada es un ejercicio que debe ser tomado como un ensayo
general, antes de llevar a cabo la estimación total del área.
38

39
FIGURA N° 25 BLOQUE O ZONA V
5.2. CÁLCULOS DE LOS ESTADISTICOS
Para determinar la calidad del modelo de variograma empleado y del plan de
krigeage empleado, es necesario calcular algunos estadísticos:
A = (1/N) Σ εi
B = (1/N) Σ( εi / Z’v)
C = (1/N) Σ [ ( Z’v - Zv) / σε]2
Donde:
• Zv es el valor observado
• Z’v es el valor estimado
• εi = Z’v - Zv = error de estimación
• σ2
ε varianza del error
Si el modelo de variograma está correcto, se deberían cumplir las relaciones siguientes:
A ≈ 0
B ≈ 0
C ≈ 1
Con los datos obtenidos por medio de esta técnica se construye una gráfica como la que se
muestra en la fig. N° 26; se prueba si existe una buena relación entre los datos observados
y los estimados. (Coeficiente de correlación).
z(x)i
V
(Ec. 21)
39

40
FIGURA N° 26 DATOS OBSERVADOS v/s DATOS ESTIMADOS
Los datos estadísticos recogidos permiten entender mejor los resultados del estudio
geoestadístico y por ello se debe poner a la validación cruzada como una técnica más del
análisis exploratorio de los datos.
5.3. VENTAJAS Y DESVENTAJAS DE LA VALIDACION CRUZADA
5.3.1 VENTAJAS
• Es útil como indicación general de las bondades( o los posibles problemas)
asociados con el modelo de variograma escogido.
• Permite detectar los problemas más serios durante el proceso de estimación,
como problemas computacionales, errores groseros.
5.3.2. DESVENTAJAS
• No es suficientemente sensitivo como para detectar ventajas menores de un
modelo de variograma comparado con otro.
• El análisis se realiza al utilizar las muestras, lo que no permite obtener una
conclusión definitiva acerca de toda el área.
zv
∧
zv
40

41
• Al tener una malla aleatoria estratificada( o malla regular). Al remover un punto,
siempre queda mal estimado, no se puede discriminar entre 2 modelos.
• Si las muestras no son representativas del área, re-estimar con buena precisión
estas muestras no implica que el modelo de variograma permita una buena
estimación del resto del depósito.
En cualquier caso, constituye el método más común y utilizado para testificar la
bondad del ajuste del semivariograma.
5.4. CONSIDERACIONES SOBRE EL ÁREA DE BÚSQUEDA
Cuando se describió el método de estimación del inverso de la distancia, se hizo
mención a las características que debía presentar el área de búsqueda, es decir, cómo se
definía la zona de captura de los puntos que entraban a formar parte de la estimación. En
el Krigeage, es necesario volver a incidir en este tema, si cabe con mayor profundidad.
Para guiar la discusión, se puede centrar el problema en las siguientes cuestiones:
a) Forma del área de búsqueda
b) Número de muestras a capturar
c) Relevancia de las muestras
5.4.1 FORMA DEL ÁREA DE BÚSQUEDA
La morfología del área de búsqueda suele ser, normalmente, una elipse centrada en el
punto que va a ser estimado. Su orientación viene dictada por la anisotropía del esquema
de continuidad espacial, con el eje mayor de la elipse en la dirección de máxima
continuidad. Si no existe dicha anisotropía, la elipse se convierte en un círculo y la
cuestión de la orientación deja de ser, obviamente, relevante. Todo lo mencionado es para
dos dimensiones, por lo que si la estimación se produjese en tres dimensiones, habría que
cambiar, evidentemente, la elipse por un elipsoide o el círculo por una esfera.
5.4.2 NÚMERO DE MUESTRAS A CAPTURAR
El siguiente paso seria definir el tamaño de la elipse, es decir, cuántos puntos de
estimación deben incluirse en ella. La respuesta más simple establecería que tendría que
incluir algunas muestras, viniendo este aspecto condicionado por la morfología de la malla
de muestreo. En la práctica se intenta conseguir que la elipse incluya, al menos, de 6 a 12
puntos de estimación. En mallas irregulares de muestreo, la longitud de la elipse debe ser
41

42
ligeramente mayor que la distancia media de muestreo, viniendo ésta definida, de forma
muy general, por:
DMM = (St/n)1/2
donde:
DMM = Distancia media de muestreo.
St = Area total cubierta por las muestras.
n = Número demuestras.
La cuestión todavía no ha sido resuelta del todo, pues quedan algunos
aspectos que comentar. En primer lugar, cuantas más muestras se incluyan, mayor será el
número de operaciones que debe llevar a cabo el sistema de ecuaciones y mayor será el
suavizado en la estimación. En segundo lugar, si se incluyen muestras cada vez más y
más lejanas la estacionariedad puede no ser asumida, con lo que la estimación queda en
entredicho. El primer aspecto queda minimizado. En cuanto al segundo, genera que
conceptos básicos como el carácter de mejor estimador insesgado del Krigeage no se
cumplan, por lo que es necesario intentar llegar a un compromiso en cuanto al tamaño de
la elipse. Es regla común utilizar, como semi-eje de la elipse, un valor próximo al alcance
del semivariograma en la dirección considerada. De esta forma se asegura el
mantenimiento de la estacionariedad y se cumple la correcta estimación. No obstante, el
ampliar este valor no excesivamente, cuando el número de muestras es insuficiente,
mejora el proceso de estimación (Isaaks y Srivastava, 1989).
5.4.3 RELEVANCIA DE LAS MUESTRAS
Esta cuestión incide en dos aspectos. Por una parte, la posible presencia de agrupamientos
de muestras, que queda resuelta. Por el diseño del propio sistema de ecuaciones de
Krigeage, que toma en cuenta y pondera este fenómeno. Por otro lado, el segundo aspecto
hace mención a la importancia de las diferentes muestras para su inclusión en la
estimación, por ejemplo en cuanto a su pertenencia a la misma población que el punto a
estimar. Esta cuestión es casi imposible de asegurar, y menos de verificar, por lo que la
decisión debe venir acompañada de una información de tipo cualitativo. En otras
palabras, el estudio geológico completo de toda la información presente es el mejor
camino para definir qué muestras son relevantes y qué muestras no lo son, pudiendo ser
estas últimas apartadas del proceso de estimación. Este problema, en yacimientos de baja
complejidad geológica puede no ser tal, incrementándose según aumenta la dificultad de la
interpretación geológica.
42

43
6. ERROR DE ESTIMACION
El error de estimación es entendido como la diferencia entre el valor real y
el valor estimado de un punto o bloque.
(Ec. 22)
Por otra parte, la estimación Z’v de un bloque se efectúa en términos de los
valores observados Z(xi) de puntos colindantes mediante la expresión:
En que los ai verifican la condición de insesgado:
(Ec. 24)
Las ponderaciones αi serán más altos para valores z (xi) en puntos xi más cercanos
al bloque y serán más bajos en puntos más lejanos.
En la ecuación 22, como Zv es desconocido, entonces ε es desconocido, la cual se
renuncia en conocerlo en signo y magnitud. Sin embargo, se puede caracterizar
probabilísticamente el error ε, al utilizar un modelo matemático.
Se asume entonces que el error ε, es una magnitud aleatoria, es decir, una variable
aleatoria. Esta magnitud aleatoria tiene una cierta ley de probabilidad caracterizada por
una esperanza matemática mε, y una varianza σ2
. Luego la ley de probabilidad del error es
la ley normal o de Gauss (ver fig. N° 27)
Error de
Estimación Valor estimado
(conocido)
Valor real
(desconocido)
z =
∧
∑ α ( α
Ν
v i i iz x) = pesos o ponderaciones
i=1
α α α α1 + 2 + 3 +.............+ N = 1
(Ec. 23)
43

44
FIGURA N° 27 LEY NORMAL O DE GAUSS
Las siguientes áreas de la Ley de Gauss:
6.1. CALCULO DE LA VARIANZA DE ESTIMACION
La varianza de estimación se refiere a la varianza del error entendido como la
diferencia entre el valor real y el valor estimado de un punto o bloque, se supone que los
errores tienen esperanza nula.
(Ec. 25)
68% 95% 99.7%
44

45
En la práctica se utiliza un riesgo de equivocación del 5%. En otras
palabras si los errores tienen distribución normal de esperanza cero y varianza σ2
ε
-2σε ≤ ε ≤ 2σε con 95% de confianza, o bien
Zv = Z’v +/- 2σε
En todo caso la expresión teórica del valor zv desconocido está dada por:
Zv = (1/v) ∫z(x) dx (Ec.26)
Al reemplazar en la ecuación 25 queda
(Ec. 27)
Al resolver el binomio se obtiene:
que es la expresión fundamental del cálculo de σ2
ε. Donde:
• N es el número de datos
• xi son las coordenadas de los datos
• v es la geometría y el tamaño del bloque o zona v
• ϒ(h) es el variograma
• αi es el peso o ponderación que se asigna a la participación de Z(xi) en el
cálculo de Z’v
• x(ó y) es un punto variable dentro del bloque
Nota: Para el cálculo de la expresión fundamental, se supone que se conoce el modelo del
variograma.
σ ε = Ε
2
[ - ]2
Ν
∑ α (i iz x)
i=1
(1/v) z(x) dx∫
v
σ ε =
2
2
Ν
∑ αi
Ν
i j∑ α γ(j x,x)
Ν
∑ αi
i=1 i=1j=1
(1/v) (x,x) dx - (1/v )
v v
(x,y) dx dy -∫ γ ∫ ∫ γi
2
(Ec. 28)
45

46
Significados de los términos en la expresión de σ2
ε :
a. El término ϒ(xi,xj): Representa el valor de ϒ (h), siendo h el vector que une los
puntos xi, xj
b. El término (1/v) ∫ ϒ (xi,x) dx : Representa el valor medio teórico de la
función ϒ(h), ( h el vector que une los puntos xi, xj ) siendo x un punto cualquiera
variable dentro de la zona v.
En la práctica la integral anterior se calcula por discretización de v en k puntos:
xi
xj
h
xi
x
v
xi
x
v
46

47
entonces, la aproximación es:
(1/v) ∫ ϒ (xi,x) dx ≅ (1/k) Σ ϒ(hj). (Ec. 29)
Se recomienda un número mínimo de puntos dentro de v, de manera de obtener
una precisión aceptable:
• Si v es bidimensional: k ≥ 36 puntos.
• Si v es tridimensional: k ≥ 64 puntos.
c. El término (1/v2
) ∫∫ ϒ (x,y) dxdy: Representa el valor medio de la función ϒ(h),
( h el vector que une los puntos x con y) entre puntos variando dentro de v.
También se calcula por discretización de v en k puntos:
Entonces, la aproximación es:
(1/v2
) ∫∫ ϒ (x,y)dxdy ≅ (1/k)2
∫∫ ϒ(hij) (Ec. 30)
Observación: Para obtener el σ2
ε, los ponderadores αi son obtenidos dependiendo del
lugar de ubicación de las muestras que participan en la estimación.
¿Existe otra ponderación de los datos que nos proporcione un error menor?
Para poder lograr los pesos adecuados, de manera de minimizar la varianza del error σ2
ε
es necesario de introducir el método del krigeage.
x
y
hij
v
x
y
h
v
47

48
7 KRIGEAGE
7.1. DEFINICION
El Krigeage es una herramienta geoestadística cuyo objetivo es encontrar los
pesos de los ponderadores ai de manera que minimicen la varianza de estimación de
acuerdo a la geometría del depósito y al carácter de la mineralización.
El krigeage es una técnica utilizada en la evaluación de yacimientos para estimar el
valor de una variable regionalizada en un punto (o en un bloque, como se verá
posteriormente), a partir de unos factores de ponderación que trabajan de forma semejante
a como lo hacen en el inverso de la distancia. Ese valor se caracteriza por ser el mejor
estimador lineal ínsesgado de la variable. El mejor, porque los factores de ponderación se
determinan de forma tal, que la varianza de la estimación es mínima; lineal, porque es una
combinación lineal de la información; e insesgado porque, en promedio, el error es nulo,
es decir, no hay sesgo en los errores (considerando como error la diferencia entre el valor
real y el estimado). Por todo ello, junto con la información asociada que ofrece en
relación al error que se comete en la estimación, el Krigeage se puede considerar, en
general, como un método óptimo de estimación, estando su utilización ampliamente
desarrollada en todo tipo de yacimientos, especialmente en aquellos que poseen un alto
valor (oro y diamantes). Dado que el alto número de cálculos matemáticos que necesita el
Krigeage ya está resuelto con el uso de la informática, quizás el único problema que
presenta es la mayor complejidad conceptual frente a los métodos clásicos. De lo
contrario, probablemente se habría convertido en el único método de estimación viable
para la mayor parte de los yacimientos a escala mundial.
Entonces, desde un punto de vista práctico, el Krigeage tiene la importancia de
evitar errores sistemáticos, bien sea sobrestimado o subestimado el valor calculado. En
términos generales, el Krigeage asignará bajos pesos a las muestras más lejanas, y altos a
las más cercanas, pero esta regla intuitiva falla a veces en situaciones tal como:
• Transferencia de la influencia o el Efecto de pantalla Las muestras más cercanas
al bloque tienden a anular la influencia de las muestras más lejanas. La consecuencia
práctica de esta propiedad es que algunas muestras tendrán ponderaciones negativas del
Krigeage.
48

49
7.2. PROPIEDADES DEL KRIGEAGE
Hay muchas propiedades buenas asociadas con el estimador Krigeage, además de
dos obvias como el insesgamiento y la varianza mínima de estimación. Algunas de éstas
son las siguientes:
• El Krigeage calcula la varianza de Krigeage para cada punto o bloque.
• Es un interpolador exacto. En otras palabras, el Krigeage estimará todos los puntos
de datos conocidos exactamente, es decir no hay error.
• El Krigeage tiene un efecto desagrupador ( Desclustering effect) de datos durante
la estimación. Esto es muy útil cuando los datos usados para estimar la ley están
muy agrupados e irregulares.
• El Krigeage tiene un efecto selectivo, lo que permite seleccionar las muestras más
cercanas.
7.3. ECUACIONES DEL KRIGEAGE
Para obtener las ecuaciones del krigeage hay que minimizar la expresión de σ2
ε .
(Ec. 31)
pero los αi, deben verificar la condición de insesgamiento:
∑ αi = 1
El método clásico para minimizar la expresión σ2
(igualar a cero las derivadas
parciales de σ2
respecto de α1, α2, ......., αN) no asegura que la suma de los αi sea 1. En
este caso, hay que utilizar el método de Lagrange.
En el caso del Krigeage hay que considerar la expresión:
σ ε =
2
2
Ν
∑ αi •
Ν
i j∑ α γ(j x,x)
Ν
∑ αi
i=1 i=1j=1
(1/v) (x,x) dx - (1/v ) (x,y) dx dy -∫ γ ∫ ∫ γv i v v
2
A = σ2
- 2μ(α1 + α2 + α3 + ….. +αn -1)
49

50
Por lo general, el parámetro m carece de significación física. Al realizar N+1,
derivaciones sostiene el sistema de ecuaciones siguiente:
que es un sistema lineal de N + 1 ecuaciones con N + 1 incógnitas ( a1, a2, ......., aN, m),
lo cual siempre tendrá soluciones.
Se demuestra que la expresión de se2 se simplifica, obteniéndose:
(Ec. 32)
7.3.1. KRIGEAGE PUNTUAL
En algunas ocasiones, en vez de estimar la ley media de un bloque V, interesa estimar
la ley en un punto X0.
Como se ha comentado anteriormente, el krigeage opera a través de la utilización de
unos factores de ponderación. Estos factores de ponderación, para obtener el valor de la
variable, se calculan a partir de un sistema de ecuaciones, denominadas ecuaciones de
krigeage, en las que las incógnitas para resolver el sistema se obtienen a partir del
semivariograma modelizado.
α γ(1 x , x ) +1 1 α γ( α γ( μ = (1/ ∫ γ(2 Νx , x ) + ............+ x , x ) + v) x , x)dx1 2 1 N v 1
α γ(1 x , x ) +2 1 α γ( α γ( μ = (1/ ∫ γ(2 Νx , x ) + ............+ x , x ) + v) x , x)dx2 2 2 N v 2
α γ(1 x , x ) +N 1 α γ( α γ( μ = (1/ ∫ γ(2 Νx , x ) + ............+ x , x ) + v) x , x)dxN 2 N N v N
α + α +..............+ α = 11 2 Ν
σ ε =
2 Ν
∑ αi •
i=1
(1/v) (x,x) dx + - (1/v) (x,y) dx dy∫ γ μ ∫ ∫ γv i v v
50

51
Ecuaciones a considerar:
Se demuestra que la expresión de σ2
ε se simplifica, obteniéndose:
(Ec. 33)
El krigeage puntual tiene la propiedad de ser un interpolador exacto (ver Fig. N°
28) en el sentido de que si se desea estimar la ley en un punto conocido, el krigeage
proporciona la ley del dato, con una varianza σ2
ε = 0. Se dice que el krigeage puntual pasa
por los puntos ( esta propiedad no la tienen los otros interpoladores):
FIGURA N° 28 INTERPOLADOR EXACTO
α γ(1 x , x ) +1 1 α γ( α γ( μ = γ(2 Νx , x ) + ............+ x , x ) + x , x )1 2 1 N 1 0
α γ(1 x , x ) +2 1 α γ( α γ( μ = γ(2 Νx , x ) + ............+ x , x ) + x , x )2 2 2 N 2 0
α γ(1 x , x ) +N 1 α γ( α γ( μ = γ(2 Νx , x ) + ............+ x , x ) + x , x )N 2 N N N 0
α + α +..............+ α = 11 2 Ν
σ ε =
2 Ν
∑ αi
i=1
γ μ(x,x ) +i 0
xx1 x2
Interpolador de Krigeage
Interpolador de minímos cuadrados
51

52
7.3.2. KRIGEAGE DE BLOQUES
Otro tipo de krigeage más frecuentemente utilizado en la evaluación de
yacimientos es el krigeage de bloques, que opera de forma similar a como lo hace el
puntual, pero con la diferencia de que el valor obtenido se le asigna a un bloque y no a un
punto. Dentro del modelo de función aleatoria descrito anteriormente, el valor medio de
una función aleatoria en una zona determinada (bloque) es, simplemente, la media
aritmética de todas las variables puntuales aleatorias incluidas dentro de esa zona. Esta
capacidad del Krigeage de llevarse a cabo sobre un área y no sólo sobre un punto, es una
característica propia y única de este método de estimación, no compartida por otros
métodos. Aunque la forma de operar puede trasladarse a métodos como el inverso de la
distancia, los resultados no son muy consistentes (Isaaks y Srivastava, 1989).
Para determinar el valor del bloque, se lleva a cabo una discretización del área en
un conjunto de puntos (2x2, 3x3, etc.), obteniéndose, a continuación, la media entre los
diferentes valores. Un ejemplo de la importancia de los computadores en el desarrollo de
la geoestadística es que, para calcular, por ejemplo, el valor de un sólo bloque con una
discretización de 10 x l0, sería necesario resolver cien sistemas de ecuaciones, cada una de
ellos con, por ejemplo, 11 ecuaciones (suponiendo una estimación a partir de diez
valores). Y esto sólo para un bloque, siendo frecuente, normalmente, dividir el yacimiento
en centenares de bloques. Todo ello llevaría a la resolución de decenas o centenares de
miles de ecuaciones, hecho absolutamente inviable si no fuese por la ayuda de la
informática.
Por último, hay que hacer constar que los valores que se obtienen con el Krigeage
(tanto puntual como de bloques) llevan aparejados los correspondientes valores de la
varianza de la estimación (varianza del krígeage), lo que permite hacer un estudio de la
bondad de la estimación. Estos valores de la varianza del krigeage pueden,
posteriormente, ser interpelados y obtener mapas en la que se puede analizar qué zonas
presentan una mayor exactitud en la estimación, cuales poseen una mayor probabilidad de
error, etc., lo que suele ser muy necesario a la hora de establecer los planes de producción
minera.
Cuando se aplica el krigeage sobre un bloque V debería considerar todos los datos
disponibles ( krigeage completo). Sin embargo, esta situación implica cálculos muy
largos. Por esta razón se recomienda restringir la vecindad de estimación que puede ser
una esfera o círculo, o bien un elipsoide o elipse (3D y 2D).
La práctica recomienda que una vecindad contenga un promedio del orden de 8
muestras, los resultados que se obtienen serán muy buenos. (ver Fig. N° 29)
52

53
FIGURA N° 29 VECINDAD DE ESTIMACION
7.3.4. KRIGEAGE INDICADOR
El Krigeage indicador es una de las innumerables variaciones que la
Geoestadística presenta para la evaluación de yacimientos, utilizándose, cada vez más, en
el análisis de las reservas, especialmente en explotaciones de alto valor (oro). Es un
método no paramétrico en el que los valores obtenidos son convertidos a 0 y 1,
dependiendo de su relación con una determinada ley de corte. Permite estimar la
proporción de un bloque bajo estudio que tiene un determinado porcentaje de probabilidad
de encontrarse por encima de la citada ley de corte. La mejor forma de observar su
funcionamiento es con un ejemplo.
Se tiene un bloque mineralizado que ha sido evaluado por sondeos situados en sus
cuatro esquinas. El valor asignado al bloque será, si el espesor es constante, la media
aritmética de las cuatro esquinas. Pueden existir dos situaciones como las siguientes:
Bloque A: 6%, 5%, 6% y 6% - ley media = 5,75%
Bloque B: 1%, 2%, 1% y 19% - ley media = 5,75%
Si la ley mínima de corte es, por ejemplo, del 5%, está claro que ambos bloques son
explotables, independientemente de que la asignación de explotabilidad del bloque B sea
casi totalmente dependiente de un único valor (19%), lo que no se refleja directamente en
el resultado.
Considérese ahora que la mineralización y el estéril son materiales con ley superior e
inferior, respectivamente, a una determinada ley mínima de corte (5%), por lo que se les
asigna un valor 1 al primer caso y cero al segundo. Entonces se tendría que, para el
bloque A, todos los sondeos entrarían en la categoría de mineralización y se le podría
asignar, al bloque, un indicador medio de 1. Por el contrario, para el bloque B, sólo un
V
53

54
sondeo entraría en la categoría de mineralización, por lo que recibiría un indicador medio
de 0,25. En este caso (bloque B), aunque la ley media sugiere que todo el bloque es
mineralización, el indicador medio nos afirma que tan sólo el 25% del bloque se puede
considerar como mineralización. Este efecto debe ser tomado en cuenta en todos aquellos
estudios que generen cálculos de reservas, pues su no consideración puede producir, como
en el caso del ejemplo, una sobreestimación de los tonelajes de la mineralización.
La expresión matemática para una variable de este tipo sería I(x,z), correspondiente a
una ley z(x) de una muestra en un punto x y con una ley de corte z. De tal forma que:
1, si Z(X) > z
I(X,Z) =
0, si Z(X) < z
Una vez que las leyes, o cualquier otra variable a estudiar, han sido transformadas de
esta manera, se puede intentar construir un semivariograma experimental y ajustarle un
modelo matemático de los existentes. Para el caso de] modelo esférico, la ecuación sería:
γ(h,z) = I0 + I [1.5(h/a) - 0,5(h/a)3
] para h < a
γ(h,z) = I0 + I para h > a
Donde I0 e I son equivalentes a C0 y C, en un semivariograma normal. Una vez que el
semivariograma de indicadores está modelizado, se puede llevar a cabo un krígeage de
bloques, que recibiría el nombre de ktigeage indicador. El valor que saliese para cada
bloque vendría a representar el porcentaje recuperable de mineralización que tiene ese
bloque para una determinada ley de corte. Los resultados pueden ser comparados con
los valores obtenidos en un Krigeage de bloques normal, con otros Krigeages
indicadores para otras leyes de corte, etc., con el fin de obtener estrategias de
explotación.
7.8. EL COKRIGEAGE
El Co-Krigeage constituye, al igual que el Krigeage indicador, otra de las
aplicaciones del Krigeage a la estimación de variables. Hasta el momento, el krigeaje
utilizaba, como parámetros para realizar la estimación, los valores de una variable. Sin
embargo, suele ser frecuente, en minería, conocer no sólo una variable sino varias de
ellas, que, usualmente, están relacionadas entre sí (pAg y Pb/Zn). Por tanto, resulta
interesante utilizar la información suministrada por una de las variables para calcular la
otra, siempre y cuando, obviamente, exista una relación entre ambas. Este proceso se
denomina, en Geoestadística, Co-Krigeage.
54

55
El Co-Krigeage pues, se define como un método de estimación que minimiza la
varianza de la estimación utilizando la correlación entre varias variables, estando los
estimados obtenidos tanto a partir de las variables secundarias como de la principal. La
utilidad de la variable secundaria muchas veces se ve incrementada por el hecho de que
la variable principal pueda encontrarse submuestreada en algunas zonas del yacimiento.
El valor estimado de una variable por Co-Krigeage viene definido por la siguiente
expresión:
Uo = Σai Σui + ΣbjΣvj
donde:
U0 = Valor del estimado en el punto 0
ui = Los datos de la variable principal en n puntos
vj = Los datos de la variable secundaria en m puntos
ai y bj = Los factores de ponderación a determinar para resolver los sistemas de
ecuaciones.
Como se puede observar, el aspecto de la expresión es muy similar a la que
correspondería para el Krigeage. De hecho, el desarrollo del sistema de ecuaciones del
correaje es idéntico al correspondiente para el Krigeage. Por tanto, prácticamente todo lo
expuesto para un método (ktigeaje) es válido para el otro (co-krígeage), en relación a los
modelos de funciones aleatorias, cálculo del semivariograma, áreas de búsqueda, etc.
Unicamente merece la pena comentar que existen ciertas situaciones en las que
este método no mejora los resultados que se obtendrían utilizando simplemente el
krígeage. Cuando los modelos de semivariogramas son muy similares entre sí, y las
variables principal y secundaria están igualmente maestreadas en todos los puntos, los
resultados con un método y otro son, prácticamente, semejantes.
55

56
LLLIIINNNEEEAAALLL ...
PPPAAARRRTTTEEE 222
EEEJJJEEERRRCCCIIICCCIIIOOOSSS ---TTTAAALLLLLLEEERRREEESSS
56

57
GGGUUUIIIAAA DDDEEE TTTRRRAAABBBAAAJJJOOO 111
CCCOOONNNCCCEEEPPPTTTOOOSSS GGGEEENNNEEERRRAAALLLEEESSS
57

58
TEMA 1
Esperanza Varianza, covarianza, histograma efecto de soporte, efecto de información
1.1.-La varianza de una V.A . Z de densidad de probabilidad f(x) esta definida por
V[Z]=E [(Z-μ)²]
Con
μ =E[Z] = ∫ z f(z)dz
Demuestre
V[Z]=E [Z²]= {E[Z]} ²
1.2.- Z Es una variable aleatoria, λ es una constante
Demuestre E [λ Z ] = λ E [ Z]
Demostrar V [λ Z ] = λ² E [ Z]
1.3.-L a covarianza centrada entre dos variables aleatorias Z1 y Z2 esta definida por
Cov(Z1,Z2) = E [ (Z1-μ1) (Z2-μ2)]
Con μ1 = E[Z1] y μ2= E[Z2]
Demuestre Cov (Z1,Z2) = E [ Z1 Z2 ] –E[Z1] E[Z2]
Demuestre Cov (Z2,Z1) = Cov (Z1,Z2)
Demostrar Cov (Z1,Z, = V(Z1)
1.4.-Z1 y Z2 son dos variables aleatorias de covarianza centrada Cov ( Z1, Z2)
Demuestre V[ Z1 + Z2 ] = V[Z1] + V[Z2]+ 2Cov(Z1,Z2)
1.5.- Sean n variables aleatorias Z1 , Z2 , …..Zn y sean n coeficientes λ1, λ2….. λn
Sabemos Z*= ∑ λi Zi
58

59
Demuestre
V[Z*]= Z*= ∑ ∑λi λj Cov( Zi , Zj)
i j
Recuerde Z* ² = ∑ ∑λi λj Zi Zj
i j
Demuestre V[ Z*] = ∑ λi ² V[Zi] + ∑ ∑λi λj Cov ( Zi , Zj)
i i =1 j<>1
Demuestre V[ Z*] = ∑ λi ² V[Zi] +2 ∑ ∑λi λj Cov ( Zi , Zj)
i i=1 j=i+1
1.6.-Aplicación: Influencia del muestreo sobre los cálculos de medias , varianza y
histogramas
Se desea hacer un estudio sobre un sitio que en el pasado tuvo residuos mineros, el
principal contaminante que queda en el terreno es un leve porcentaje de ácido remanente
Se ha decidido hace una primera campaña de muestreado en cuadros de 10 x 10 metros
A.- Campaña 1
90 39
80 33 43 33
70 32
60 26
50 28
40 35
30 29
20
10
0
0 10 20 30 40 50 60 70 80 90
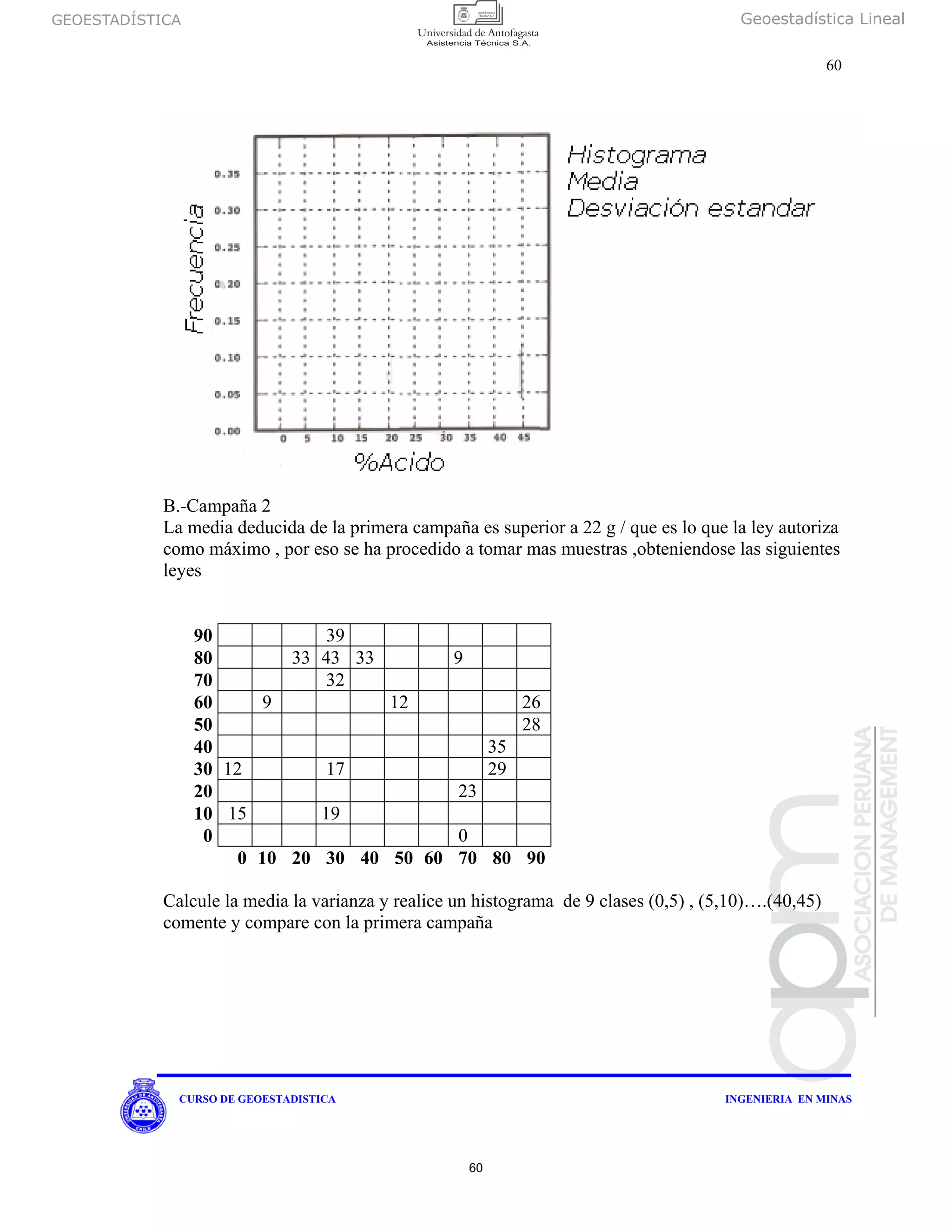
Calcule la media la varianza y realice un histograma de 9 clases (0,5) , (5,10)….(40,45)
59

60
B.-Campaña 2
La media deducida de la primera campaña es superior a 22 g / que es lo que la ley autoriza
como máximo , por eso se ha procedido a tomar mas muestras ,obteniendose las siguientes
leyes
90 39
80 33 43 33 9
70 32
60 9 12 26
50 28
40 35
30 12 17 29
20 23
10 15 19
0 0
0 10 20 30 40 50 60 70 80 90
Calcule la media la varianza y realice un histograma de 9 clases (0,5) , (5,10)….(40,45)
comente y compare con la primera campaña
60

61
C.- Campaña 3
Teniendo en cuenta la importancia de la dispersión de las leyes ,se ha decidido efectuar un
muestreo sistemático ,cada cuatro parcelas ,dando el siguiente resultado:
90
80 21 43 20 9 12
70
60 9 25 12 20 26
50
40 30 11 19 19 17
30
20 23 15 15 23 14
10
0 25 2 23 0 12
0 10 20 30 40 50 60 70 80 90
Realice los mismos cálculos anteriores
61

62
D.-Mas tarde con un muestreo en todo el sector se tendra , lo siguiente :
90 22 20 15 39 20 22 10 4 12 7
80 30 21 33 43 33 20 14 9 4 12
70 24 23 13 32 29 24 24 11 6 16
60 30 9 7 25 24 12 26 20 16 26
50 23 16 14 11 23 19 14 16 12 28
40 18 30 21 11 23 19 8 19 35 17
30 12 45 21 17 14 18 15 19 29 19
20 11 23 27 15 11 15 26 23 15 14
10 15 13 10 19 28 25 24 8 14 6
0 20 25 21 2 24 23 21 0 19 12
0 10 20 30 40 50 60 70 80 90
62

63
Si usted observa este grafico y los anteriores cual es su comentario , Comente y discuta
con sus compañeros
1.7.- Efecto de soporte de las muestras sobre la varianza y histograma
Siempre en nuestro sitio ,,las nuevas parcelas se denominaran V y seran constituida de 4
pequeñas parcelas v ,ellas miden 20 x 20 (con todos los datos) , si calculamos los valores
de 1.6 se tendrá los siguientes valores
63

64
Calcule la media , la desviación estandar de estos datos y trace un histograma
experimental y compare
64

65
1.8.-Efecto Información
Si usted debe tomar la decisión sobre el terreno a partir de la campaña 3 ,tenemos el
iguietne plano
90
80 21 43 20 9 12
70
60 9 25 12 20 26
50
40 30 11 19 19 17
30
20 23 15 15 23 14
10
0 25 2 23 0 12
0 10 20 30 40 50 60 70 80 90
Recuerde que un sector es considerado habitable si el congtenido de acido es menos a 22
grs / ton
Conteste
a.- Parcelas estimadas contaminadas y en la realidad están contaminadas
b.- Parcelas estimadas no contaminadas y en la realidad están no contaminadas
c.- Parcelas estimadas contaminadas y en la realidad están no contaminadas
d.- Parcelas estimadas no contaminadas y en la realidad están contaminadas
65

66
Realice una nube de correlación
66

67
VVVAAARRRIIIOOOGGGRRRAAAFFFIIIAAA
67

68
Tema 2: Covarianzas y variograma teórico y experimental
2.1.-Z(x) es una función aleatoria estacionaria de esperanza m , de covarianza C(h)
C(h) = Cov ( Z ( x + h ) , Z ( h ) )
= E [ ( Z ( x + h ) – m ) ( Z ( x ) – m ) ]
Demuestre C(0)>=0
Demuestre C(-h)=C(h)
Demuestre /C(h)/<=C(0)
2.2.-Z( x ) es una función aleatoria intrinsica de variograma g (h)
g (h) = ( ½ )* E [ Z ( x + h ) – Z ( x ) ]2
= E [( Z ( x + h ) – m ) ( Z ( x ) - m) ]
Demuestre g (h) = (1/2) V [ Z ( x + h ) – Z ( x ) ]
Demuestre g (h) >= 0
Demuestre g (0) = 0
Demuestre g (-h) = g (h)
2.3.-Z(x) es una función aleatoria estacionaria, de covarianza C(h)
Demuestre g ( h ) = C ( 0 ) – C ( h )
2.4.-Z(x) es una función aleatoria estacionaria λ 1 , λ2 , λn de coeficientes constante , u1
u2 u3….un , las ubicaciones en el espacio .
Si
Z*
= Σ λi Z(ui)
Recuerde que
V(Z*)= ΣΣ λi λj Cov(Z(ui), Z(uj))
Demuestre que si Σ λi = 0
68

69
Entonces
V(Z*)= -ΣΣ λi λj g (Z(ui), Z(uj))
2.5.- Z(x) es una función estacionaria de covarianza C(h) y de variograma g (h)
esférico :
ahsi
a
h
a
h
Ch 〈−= )
3
3
*
2
1
*
2
3
(*)(γ
= c si h>=a
Si tenemos Z*= Z(u1) +Z (u2 ) con pesos u1 y u2 distante a 100 mts.
• ¿Puede escribir V(Z*) directamente con la ayuda de g(h) ?
• Entregue una expresión para V(Z*)
• Calcule V(Z*)con una meseta C=3 y un alcance a=250 mts.
• Calcule V(Z*)con una meseta C=3 y un alcance a=25 mts.
• Explique la diferencia
2.6.-si se tiene
69

70
• Podemos escribir V(Z*) directamente con la ayuda de los de g(h) ?
• Calcule V(Z*) cuando la covarianza es exponencial
)
200
exp(*5.2)(
h
hC −=
El variograma esferico es:
200)
3200
3
*
2
1
200
*3(*2)( 〈−= hsi
hh
hγ
g (h)= 4 si h >= 200
• Cual es la meseta y el alcance estos variograma
• Calcule la V(Z*)
2.7.- A provisto de la distancia h y de ciertas confusiones posibles ,tenemos
• Dos medidas z(u1) y z(u2) en un espacio a una dimensión ,¿cual es la distancia h de
separación? .
• Dos medidas z(u1) y z(u2) en un espacio a dos dimensiones u1=(x1,y1) y u2=(x2,y2)
,¿cual es la distancia de separación?
• Dos medidas z(u1) y z(u2) en un espacio a tres dimensiones u1=(x1,y1,z1) y
u2=(x2,y2,z2) ,¿cual es la distancia de separación?
70

71
2.8.- Z(x) es una variable aleatoria conocida en 48 nodos de hungarilla regular de paso 1
metro .En cada nodo xi asociamos un peso λi representado sobre la figura (pesos igual a
+1 y -1 )
Si
48
Z*=∑λi Z(xi)
i=1
71

72
y cometemos el error de considerar ,a 2 dimensiones ,el variograma siguiente
2)( 〈= hsihhγ
2)( ≥= hsihhγ
denominandose lineal por pedazo ,que no es admisible que a 1 D
• Sobre el grafico siguiente trace el variograma y el covariograma
2.9 Variograma esferico recordemos la formula :
ahsi
a
h
a
h
Ch 〈−= )
3
3
*
2
1
*
2
3
(*)(γ
= C si h >=a
• Usando el grafico de la página siguiente, trace un variograma con meseta 2 y
alcance 100 metros.
• Calcule la derivada g’ (h)del variograma g (h)
• Demuestre que la tangente de g (h) para h=0 corta la recta de la ecuación y=C en
h=(2/3)*a.
72

73
• Demuestre que el comportamiento de g (h) en el origen es idéntico al
comportamiento del variograna lineal
)*
2
3
()( h
a
C
h =γ
• Siempre en el mismo grafico trace un variograma que sea la suma de dos
variogranas esféricos de alcance a1=50 ,a2=100 m ;la meseta C1=C2=1 (para h> =0)
2.10 Variograma exponencial recordemos la formula
))exp(1(*)(
a
h
Ch −−=γ
• Siempre sobre el mismo grafico trace el variograma C=2 y a = 30 m ,compare con
los anteriores variogramas
• Por definición el alcance practico de un veriograma es la distancia donde g (h) es
el 95 % de su meseta C .Calcule el alcance practico de un variograma exponencial.
• Calcule la derivada de g’(h) , del variograma g (h)
• Demuestre que la tangente de g (h) para h=0 corta la recta de la ecuacion y=C em
h=a
2.11.-Variograma gaussiano recordando la formula
))
2
2
exp(1(*)(
a
h
Ch −−=γ
• Siempre sobre el mismo grafico trace el variograma C=2 y a = 50 m ,compare con
los anteriores variogramas
• Desarrolle limite de la función exp(x) para x proximo a 0 es
....
!
....
!2
2
1)exp( +++++=
n
nxx
xx
73

74
• Calcule el desarrollo limite del variograma para h próximo a 0 ,deduciendo que el
variograma gausiano posee un comportamiento parabólico en el origen .
74

75
2.12 .-Variograma experimental a 1 dimensión .Dos series de leyes z1(p) y z2(p) .Los
datos son a un metro y p representa la cota de la ley calculada a partir del collerin del
sondaje .
• Para los dos sondajes ,las leyes utilizadas son las mismas .Que puede usted deducir
,concerniente a las medias y a las varianzas de leyes en cada sondaje (sin calcular)
• Para ambos sondajes las leyes son las mismas ,pero su disposición es diferente
.Utilizando el grafico siguiente calcule el variograma experimental de leyes a los
largo de cada sondaje ,haciendo variar p , limítese a h<5 m.
75

76
2.13.-Variograma experimental a dos dimensiones Volvamos sobre nuestro viejo sector
minero
Calcule los variograma horizontales y verticales Yy reportelo sobre el grafico siguiente
76

77
Compare este variograma con el de grafico inferior, comente
77

78
VVVAAARRRIIIAAANNNZZZAAASSS
78

79
Tema 3 Cálculo de varianza de dispersión
Dispersión de un punto en un volumen
Una función aleatoria Intrínseca Z(x), de variograma γ(h) donde se conocen las
realizaciones z(x) sobre un volumen V esta dado por
1)(
1
−=
∫ fduuz
V
Vm
La varianza de los valores z(x) en el interior del volumen V esta dada por
22))((
1
)(2 −−=
∫ fduVmuz
VV
OS
Si ahora consideráramos todas las realizaciones posibles z(x) de la Función aleatoria Z(x),
la varianza de la Funciona aleatoria Z(x) en un volumen V esta definida por
32))((
1
)(2()(2 −−==
∫ fduVmuz
VV
OSE
V
Oσ
σ2
(0/V) es llamada varianza de dispersión de Z(x) en V
4),()(
2
1
)(2 −=−=
∫∫ fVVdv
V
vu
V
du
V
V
O γγσ
Para poner en marcha estas formulas , uno de los primeros problemas es que solo se
conoce un numero limitado de “N” muestras z(xn)
Para ello recurriremos a las siguientes formulas
´1
1
)(
1* −
=
=
∑ f
N
n
nxz
N
Vm
79

80
Donde N es el numero de muestras contenidas en el volumen V
´2
1
2)*)((
1
1*)(2 −
=
−
−
=
∑ f
N
n
Vmnxz
NV
OS
Figura 1
Otro problema típico es cuando se conoce realizaciones de la función aleatoria , pero en
diferentes volúmenes “K” de igual tamaño VK , figura 2
80

81
Figura 2
Vamos a aceptar de aproximar las formulas 3 por la siguiente
´3
1
*)/(21
)(2()(2 −
=
==
∑ f
K
k
kVOS
KV
OSE
V
Oσ
Con K: Numero de bloques Vk en el yacimiento G, y calculamos S2
(O/VK )*
de los
volúmenes Vk disponibles , con los promedios.
Sobre el yacimiento G cubierto por los volúmenes VK obteniendo también una
aproximación de la dispersión de un punto sobre un volumen V .Esta Aproximación será
mejor si los volúmenes Vk son numerosos y en cada volumen Vk ,los puntos son
numerosos .Si conocemos γ(h) los cálculos son mucho mas simples dado a que se resumen
a la aplicación de la formula 4 , y para ellos se puede recurrir a los ábacos ., estos
entregaran los valores de γ(V,V) promedio .
Aplicación
3.1.-Se tiene un sitio con contaminación de acido en el suelo, se desea reconvertir este
lugar en sitio urbano, los resultados de las muestran están en la figura 3
Consideraremos que estas medidas son puntuales Su valor medio es de 18.8 con una
desviación estándar de 8.48.
81

82
• ¿ Valor m*
G ? ( Sin calculo)
• ¿Valor de σ2
(0/G)*
? (Sin calculo )
3.2.-Considere 4 sectores Vk que miden 40 x 40 no utilice los datos de la parte rayadas
Calcule σ2
(0/V)*
procediendo en orden ( meta los resultados en la figura , le ayudara)
Para cada celda Vk calcule mVk
*
y S2
(0/V*
k) (Formula (1’) y (2’))
Calcule σ2
(0/V)*
(Formula (3’))
3.3.-Considerando las 25 pequeñas parcelas vk midiendo cada una 20 m x 20 m los valores
de m*
vk y S2
(0/V*
k) para cada celda los valores calculados son
82

83
• Calcule σ2
(0/v)*
• Si usted compara σ2
(0/G)*
y σ2
(0/v)*
cual es su conclusión ?
• Porque no se puede compara σ2
(0/V)*
con σ2
(0/G)*
y σ2
(0/v)*
?
3.4.- Utilización de los ábacos
Un variograma experimental de medidas z(xn) a sido ajustado a un modelo esférico de
alcance en el eje X 18 metros y en el eje Y 30 metros .
83

84
La meseta utilizada es diferente de la varianza de los datos ,eso se puede deber a no tener
suficientes puntos o que no es necesariamente estacionaria .Este ajuste es lejos perfecto ,
pero servirá por el instante.
Hasta ahora nos habíamos conformado con calcular las varianzas de dispersión
experimentales σ2
(0/V)*
, σ2
(0/G)*
y σ2
(0/v)*
utilizando las formulas de aproximación
1´, 2´, 3´ ,pero es posible calcularlas directamente con la formula
σ2
(0/V) = γ (V/V)
Para hacer los cálculos es necesario utilizar los ábacos de la función F( L,l ) .Esta función
da directamente el valor medio de un variograma de meseta 1 y alcance “a” cuando los
puntos x y x’ describen independientemente el rectángulo V =L x l
84

85
En este caso las cosas son un poco mas complicadas porque γ (h) no es isotropico, es
necesario calcular L/a1 y l/a2 para poder leer el ábaco, posteriormente se multiplica este
valor por la meseta.
Para las celdas V sucesivamente iguales a G, V v calcule por este método σ2
(0/V) ,
σ2
(0/G) y σ2
(0/v),
,Usted puede utilizar la tabla siguiente
• ¿Compare estos resultados, cuales son sus conclusiones?
• ¿Si considera ahora una meseta de 72, los resultados mejoran? , ¿Cuales son sus
Conclusiones?
85

86
3.5.- Nuevo ajuste del variograma ,
Se ha decidido, cambiar el ajuste del variograma, por un varigrama experimental
adoptando un modelo anidado, compuesto de dos estructuras
γ (h) =γ1(h)+ γ2 (h)
γ1(h) = Efecto pepita de valor C0 = 8
γ2(h) =Esférico anisotropico de C1=67 a1=18 a2= 30
86

87
• ¿Cuale seria la expresión g(V,V)?
• Rehaga lso calculos con este nuevo modelo
• Compare los modelos precedentes (Modelo esférico anisotropico de alcance 75),
¿Finalmente que modelo eligiria usted ?
87

88
LA RELACION DE KRIGE
Si tenemos que v subconjunto de V la varianza de dispersión Zv (x) cuando x describe a V
en una expresión
σ2
(v,V) = γ (V,V) –γ(v,v)
Esta formula es valida sin importar el volumen v en V de un punto hasta el yacimiento G
,la sola regla a respetar sera
GVvx ⊂⊂⊂
σ2
(v/G) = γ (G,G) –γ(v,v)
En esta expresión se puede hacer aparecer γ(V,V)
σ2
(v/G) = γ (G,G) –γ(V,V) + γ (V,V) –γ(v,v)
Esto nos entrega la formula de M. Krige .
σ2
(v/G) = σ2
(V/G) + σ2
(v/V)
3.7 Verifique la formula de M.Krige para σ2
(0/G)
88

89
VARIANZA DE ESTIMACION LOCAL
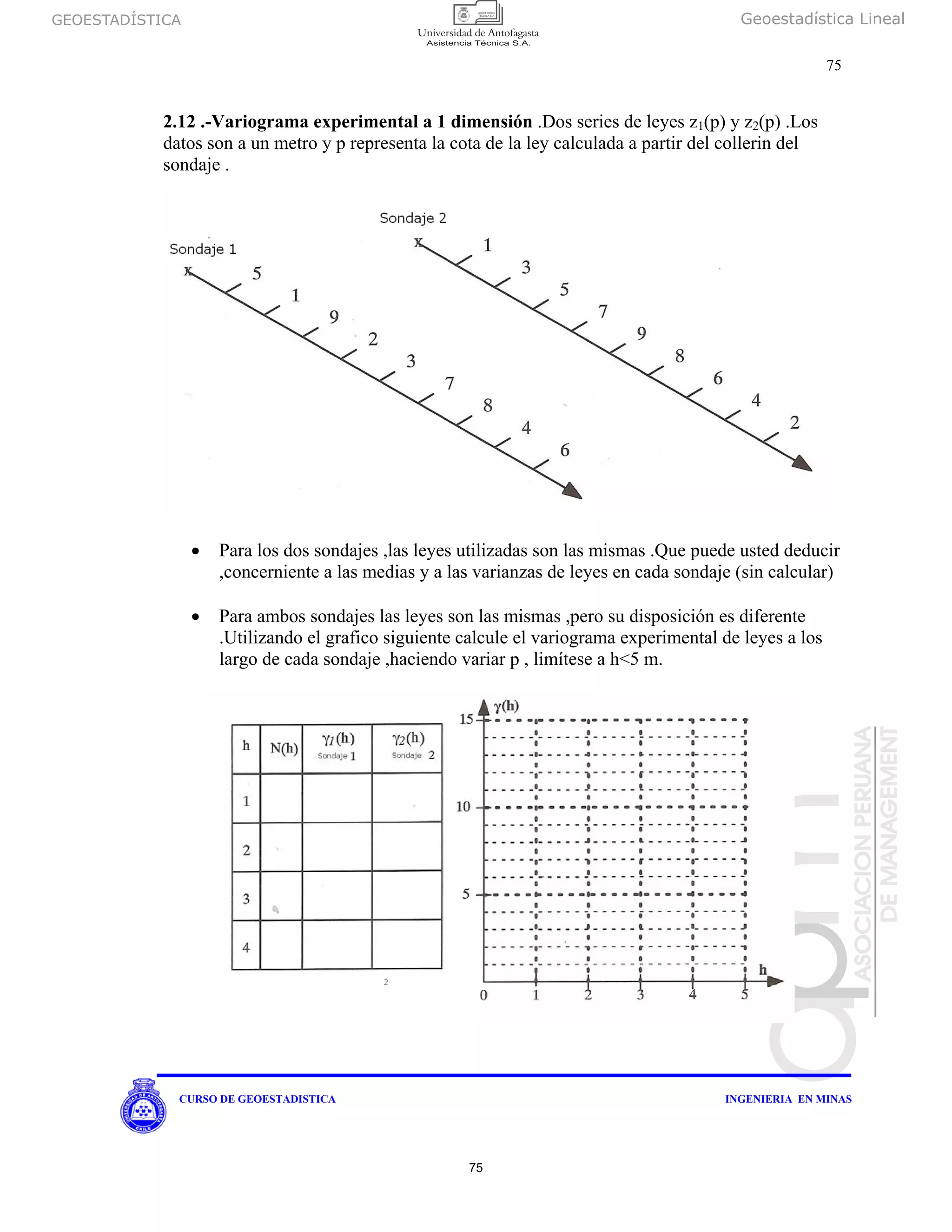
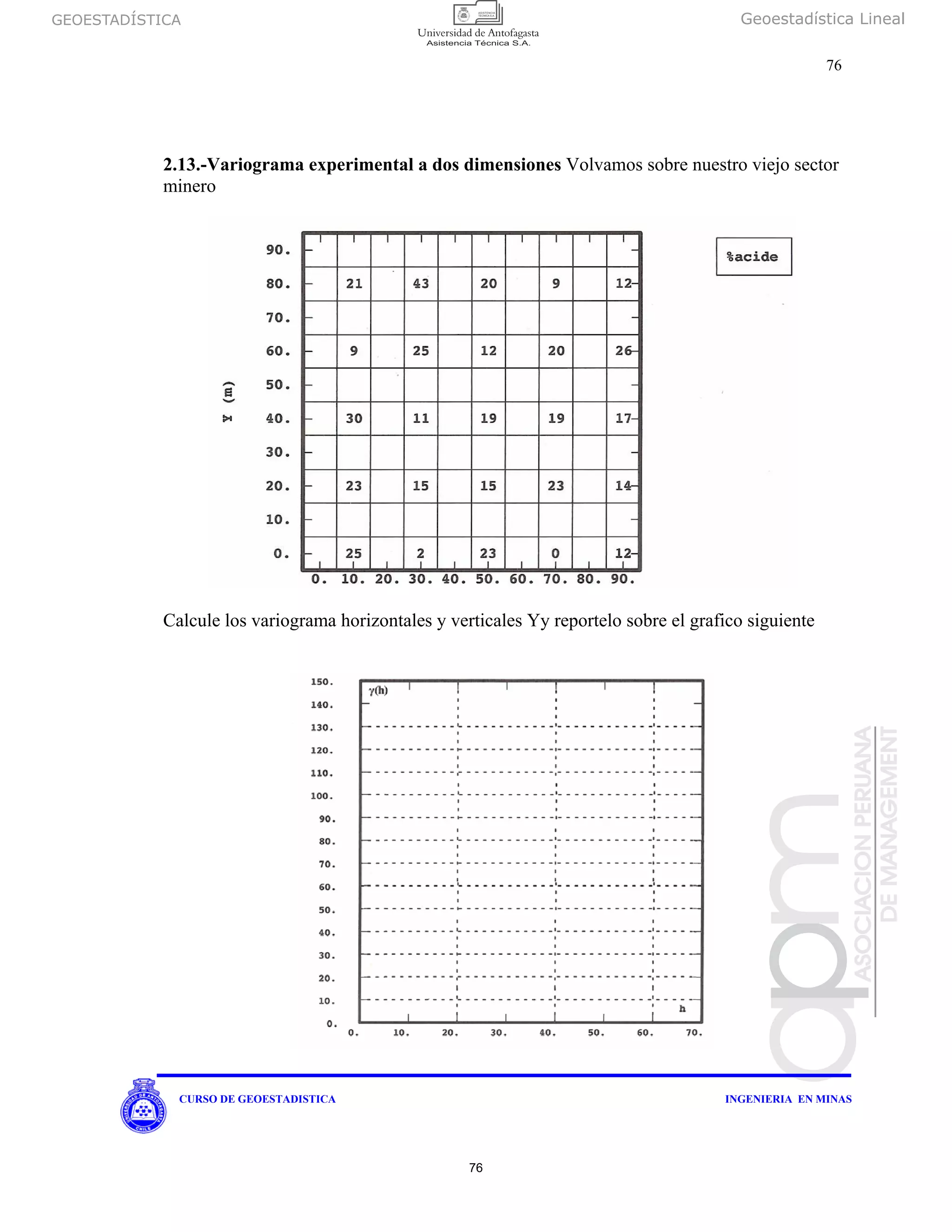
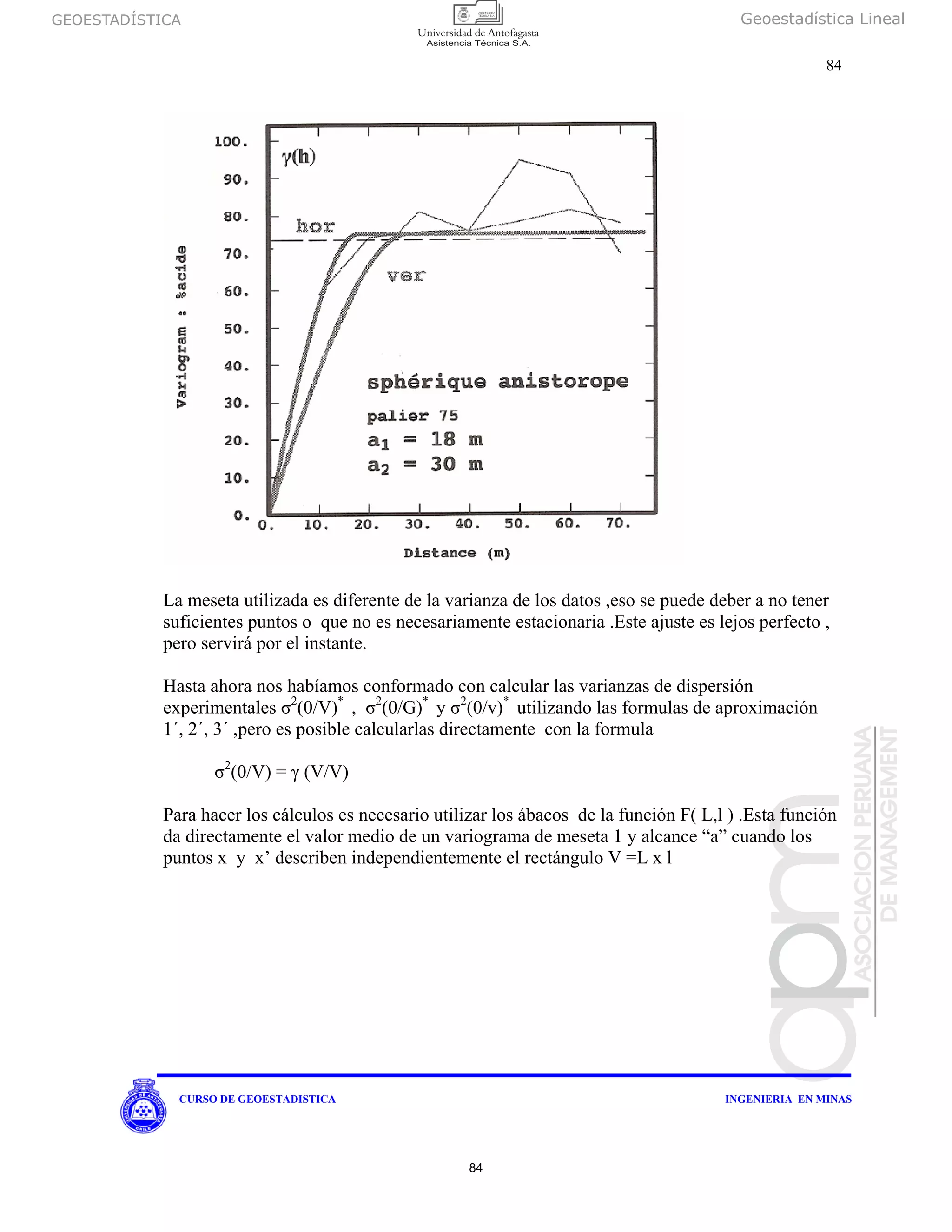
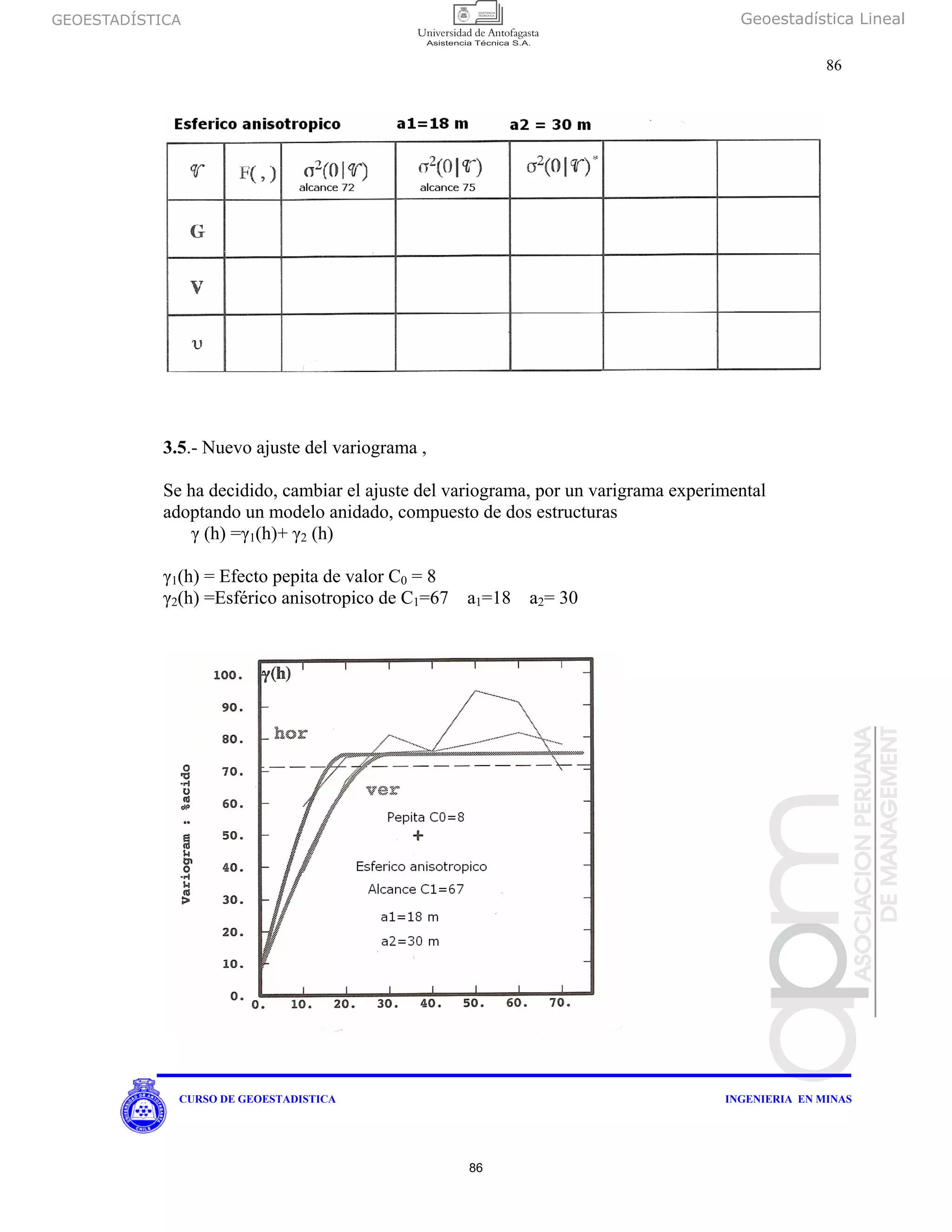
Z(x) es una función aleatoria intrínseca de variograma g (h) y V un volumen .Cuando
reemplazamos
∫=
)(
)(
1
)(
xV
duuZ
V
xvZ
Por un estimador ZV(x) cometiendo un error aleatorio (ZV(x) –ZV(x)*
) , por lo tanto será
una medida importante de la varianza , que llamaremos varianza de estimación
)*]()([2 xVZxVZV −=σ
Si el estimador ZV(x) es no sesgado .es decir que su error (ZV(x) –ZV(x)*
) es de esperanza
nula ,entonces
]2)*)()([(2 xVZxVZEE −=σ
Este estimador puede ser
La media de Z(x) sobre otro volumen v que no es necesariamente incluido en V
∫=
)(
)(
1
)(
xv
duuZ
v
xvZ
),().(),(*2),'(2 VVvvVvVvE γγγσ −−=
89

90
Podemos utilizar muchos ejemplares de volúmenes v(xk) promediando las cantidades
Zv(xk) que estan asociados ,entonces
Estos volúmenes pueden ser reducidos a puntos con media de cantidades Z(xk) , tenemos:
Estas varianza del error que son las varianzas de estimacion .se calculan con las ayudas de
los abacos como para las varianzas de dispersión ,sabiendo que :
Aplicación Varianzas de estimacion local
Para los calculos emplearemos un modelo γ(h) esferico isotropico de meseta C y de
alcance 9 metros
3.8.-Estimemos Z(x) por Z*(x) =Z(x+h)
• ¿Entrege la formula teorica de la varianza de estimación σ2
E(x, x+h)?
• ¿Valor de σ2
E(x, x+h) para h= 10 ?
• ¿Valor de σ2
E(x, x+h) para h= 3 y C=1?
90

91
3.9.-V es un rectangulo de 10 x 10 estime ZV(x) por ZV(x)*= Z(x0) ,estando x0 en el centro
de V .
• Entregue la formula teórica para la varianza de estimación σ2
E(0, V)?
• Utilizando los ábacos calcule σ2
E(x, x+h) cuando C=1
• Cual es resultado dado por el calculo directo en el ábaco
3.10.-El mismo rectangulo estime ZV(x) * = (1/4)*Σ(Z(xk) ,la media de las medidas
situadas en las extremidades .
• Entregue la formula teórica de la varianza de estimación σ2
E({xk}, V)?
• Utilizando los ábacos calcule σ2
E({xk}, V) cuando C=1
• Cual es el resultado directo
• Comparando con el anterior , que configuración elegiría usted
91

92
VARIANZA DE ESTIMACION GLOBAL
Sea Z(x) una funcion aleatoria conocida sobre un dominio
iV
N
i
UG
1=
=
La media global sera
∫=
G
duuZ
G
GZ )(
1
Será estimada por
**
1
1*
ivZ
N
i
iV
G
GZ
∑=
=
Con Z*
Vi , estimacion local de la media sobre Vi .Deseando cuantificar la varianza del
error cometido
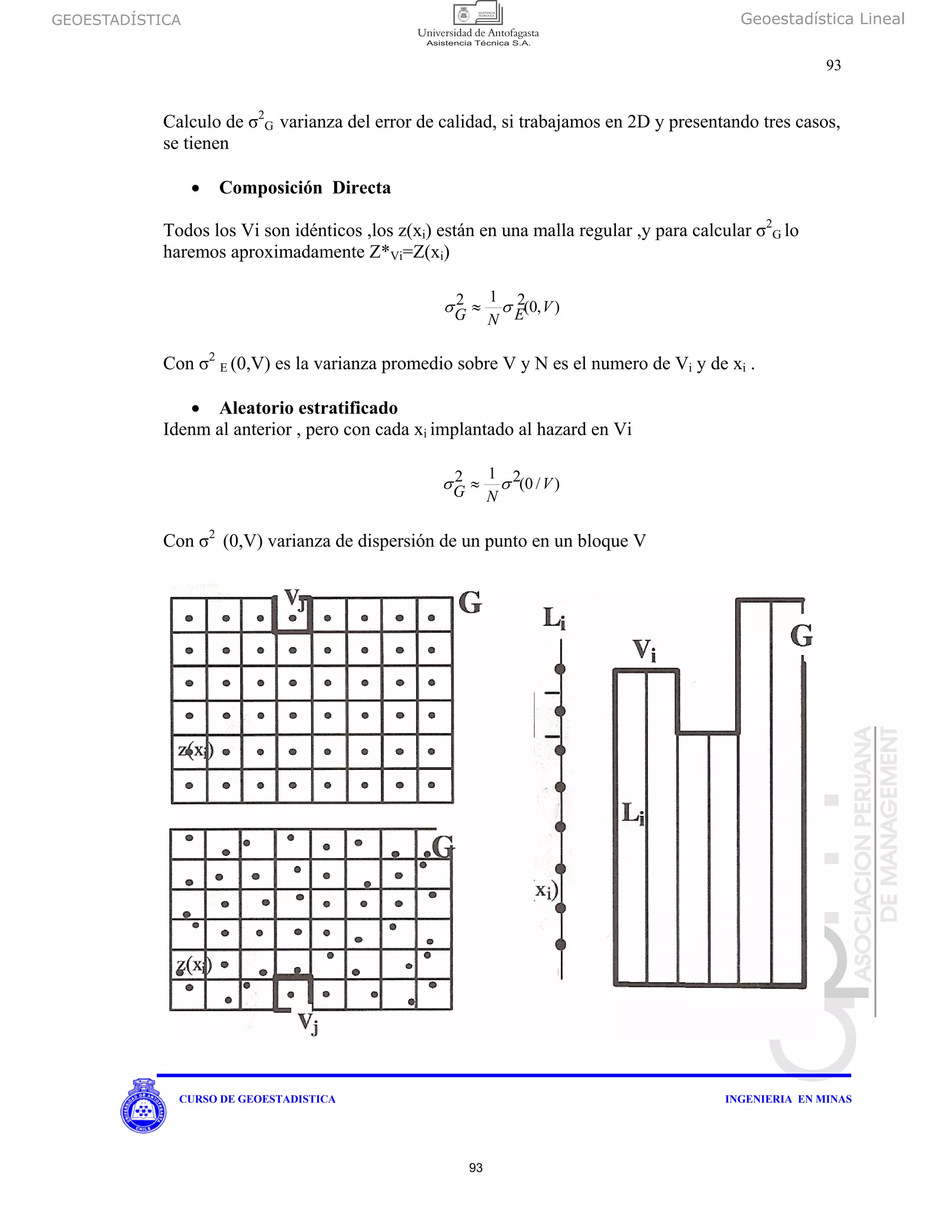
globalestimacionianzaGZZVT var]*[2 −=σ
Si desarrollamos esta expresión se obtiene:
92

93
Calculo de σ2
G varianza del error de calidad, si trabajamos en 2D y presentando tres casos,
se tienen
• Composición Directa
Todos los Vi son idénticos ,los z(xi) están en una malla regular ,y para calcular σ2
G lo
haremos aproximadamente Z*Vi=Z(xi)
),0(212 VENG σσ ≈
Con σ2
E (0,V) es la varianza promedio sobre V y N es el numero de Vi y de xi .
• Aleatorio estratificado
Idenm al anterior , pero con cada xi implantado al hazard en Vi
)/0(212 V
NG σσ ≈
Con σ2
(0,V) varianza de dispersión de un punto en un bloque V
93

94
• Composición linea - panel
G es una reunion de un conjunto de N paneles rectangulares Vi reconocidas por trazos
medios Li ,Haremos una aproximación Z*Vi=Z(Li)
∑
∑
=
=≈
N
i
iV
N
i
iViLEiV
Panel
1
2
1
),(2*2
2
σ
σ
Con σ2
E(Li,i)=Varianza de estimación de la media sobre Vi por la media sobre Li ,y N el
numero de Vi .
Cada línea Li es reconocida por una sucesión de Z(xi) espaciadas a distancia constante l
.Hacemos una aproximación que Z*li=Z(Li) ,donde
),0(212 lEMLinea σσ ≈
Con σ2
E(0,l)=varianza de estimacion de segmento l por un ppunto y M el numero total de
muestra Z(x) en G
La varianza de estimacion global esta compuesta de dos terminos
222
lineapanelG σσσ +≈
• Calculo del error geométrico
Si consideramos
iV
N
i
G
U1=
=
94

95
Donde los Vi son todos identicos , no se conoce la geometría del dominio G mas que por
aproximación de los datos asociados a Vi que indicarian una mineralizacion .Si contamos
su cantidad esta es N , lo que entregaria una area aproximada de A* =N*V
La varianza del error cometido sera
)
2
2
1*061.0
6
2(
2
1
2
2
N
NN
NA
A +≈
σ
Con N numero total repuntos estimados como mineralizados
)
2
,
2
(1
HorizonalNVerticalN
SupN =
)
2
,
2
(21
HorizonalNVerticalN
InfN =
NVer=numero de segmentos verticales sobre los bordes estimados
NHor=numero de segmentos horizontales sobre los bordes estimados
)/0(2
2
2
2 GE
A
A
B σ
σ
σ =
Con σ2
E(0/G)= Varianza de dispersión de los puntos en el dominio .
95

96
• Aplicación VARIANZA DE ESTIMACION GLOBAL
3.11.-Optimización del reconocimiento
Con el propósito de optimizar el reconocimiento de un panel , evaluando 4 tipos de
disposiciones de toma de muestra .Elvariograma de las muestras es la suma de un efecto
pepita de meseta 1 y de un modelo esferico de meseta 4 .su alcance es igual a= 25 m. y
a=50 m. .Las dimensiones del panel es de 90 x 120 m2
.
Se establecera que las muestras y sondajes corresponde a un mismo soporte.
• ¿Para los dos valores de a ,calcule las varianza de estimación global del panel
según los cuatro casos ,posteriormente sintetice los resultados en la tabla siguiente
,compare ,concluya ?
96

97
3.12 Error geométrico
Una superficie G reconocida por las muestras puntuales .Las muestras con mineralización
son indicadas como 1 , y las otras como 0 .La malla de reconocimiento es de 10 x 10 m.
• Calcule A* ,el área resúltate de estas medidas
• Calcule (σ2
A/ A2
)
• Traduzca esto en un intervalo de confianza sobre la hipótesis que a distribución de
los errores (A – A*) es gaussiana .
97

98
KKKRRRIIIGGGEEEAAAGGGEEE
98

99
KRIGEAGE ORDINARIO PUNTUAL
4.1.-Sean dos puntos de leyes M1 Y M2 y un punto P0 .Z(u) es estacionaria de orden 2 de
variograma g(h) ,estime Z(P) por krigeage ordinario (K.O.) utilizando M1 y M2.
• Construir las ecuaciones de Krigeage
• Resolver el sistema de ecuaciones de krigeage cuando g(h) es pepita de meseta C .
• Resolver formalmente el sistema de Krigeage cuando g(h) no es pepita
• Que advierte cuando la meseta es multiplicada por 2
Si g(h) no es pepita ,pero su alcance practico a=a1 o a2=a3 y isotropico de alcance C
99

100
• Resuelva formalmente el sistema para los tres casos
• Compare los ponderadores de M1 y M2 en los casos 2 y 3
4.2.- N puntos de medidas y un punto P0
• Escriba el sistema a resolver cuando g(h) es pepita de meseta C.
• Que pasa cuando la meseta es multiplicada por 2 .
KRIGEAGE ORDINARIO DE UN BLOQUE
4.3.-Sistema general
Si estimamos el valor medio de Z(u) por un Krigeage Ordinario utilizando los valores de
Z de los puntos Mi
100

101
• Construir las ecuaciones del K.O
• Si ocupamos estas ecuaciones a aquellas del K.O puntual ,¿Qué cambia?.
4.4.-Aplicación a una configuración particular de puntos
Un bloque achurado de 200 x 200 m2
es krigado utilizando 5 muestras dispuestas sobre
una malla regular separada 200 m .Z(x) es estacionaria de variograma isotropico g(h) .
• Escriba formalmente el sistema de ecuaciones del Krigeage .sobre forma de
ecuaciones, y sobre la forma matricial.
• Intente simplificar las ecuaciones del sistema.
El variograma de Z(x) es esférico de meseta C y de alcance 250 m.
101

102
• Simplifique el sistema para poder resolverlo formalmente
La meseta C=2
• Con la ayuda de los ábacos ,encuentre la solución ,escriba ,el estimador dando la
varianza del krigeage.
102

103
PPPAAARRRTTTEEE 333
AAABBBAAACCCOOOSSS...

104

105

106

107

108

109

110

Geoestadistica lineal

Más contenido relacionado

La actualidad más candente

Destacado

Similar a Geoestadistica lineal

Más de Ingemmet Peru

Último

Geoestadistica lineal