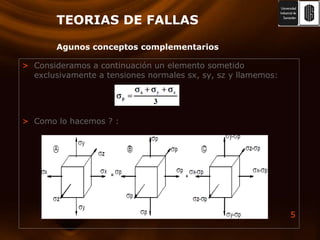
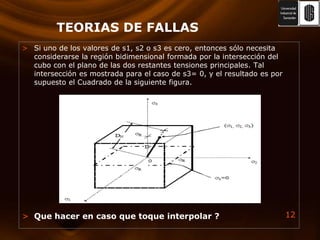
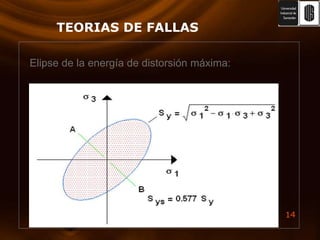
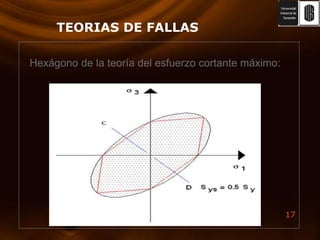
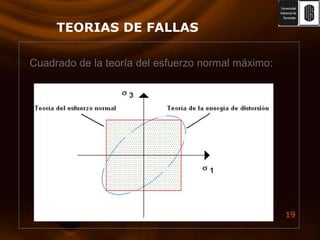
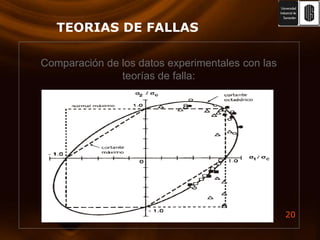
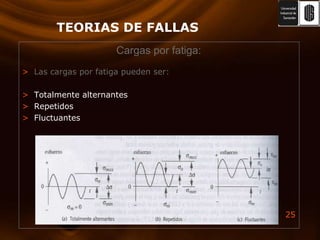
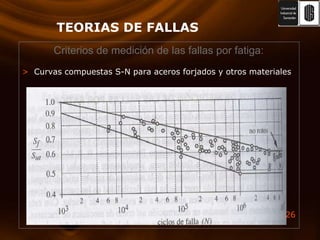
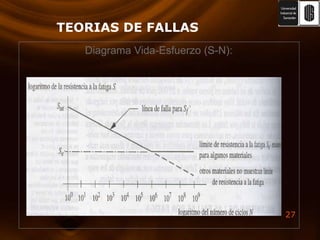
El documento presenta varias teorías de falla basadas en esfuerzos estáticos y dinámicos. Explica la energía de deformación y su relación con el módulo de corte. Luego describe las teorías de Rankine, Von Mises, esfuerzo cortante máximo y esfuerzo normal máximo. También cubre la teoría de Coulomb-Mohr y fallas por fatiga, incluyendo curvas S-N y criterios de medición. El documento proporciona una comparación completa de las teorías de falla.

1. Primer semstre de 2011GeologiaEstructuraly Del PetroleoUniversidad Industrial De SantanderLuis CarlosPatiñoLagos 2073050

2. Mayra Alejandra Mojica Barajas 2000000 TEORIAS DE FALLASAgunos conceptos complementariosEnergía total de deformaciónLa energía específica de deformación en un punto de un sólido sujeto a un estado de tensión cualquiera, es una función tanto de las tensiones actuantes como de las deformaciones. En los capítulos anteriores ya hemos analizado el valor de la energía de deformación por unidad de volumen para algunos casos simples:Las expresiones anteriores surgen de la consideración del comportamiento del material como elástico lineal, es decir, que vale la Ley de Hooke.

3. TEORIAS DE FALLASAgunos conceptos complementariosEn el caso más general de un estado triple tendremos que considerar la energía específica de deformación correspondiente a cada tensión.En el caso particular de un estado doble, la expresión anterior se reduce a la siguiente:En el estado lineal:

4. TEORIAS DE FALLASAgunos conceptos complementariosRelación entre E y G:Si en un cuerpo sometido a tensiones consideramos un elemento diferencial en una determinada posición, la energía de deformación por unidad de volumen correspondiente al mismo deberá mantenerse se la suponemos rotado.Si tenemos un prisma elemental sometido a corte puro, sabemos que a 45º de esa posición nos encontraremos en el elemento sometido a tensiones de tracción y compresión.

5. TEORIAS DE FALLASAgunos conceptos complementariosConsideramos a continuación un elemento sometido exclusivamente a tensiones normales sx, sy, szy llamemos:Como lo hacemos ? :

6. TEORIAS DE FALLASAgunos conceptos complementariosProcedimiento a seguir

7. TEORIAS DE FALLASTEORIAS DE FALLA:Componentes ingenieriles pueden estar sujetos a cargas complejas de presión, tracción, compresión,torsión, flexión, o una combinación de ellas, de forma tal que para un cierto punto del material se producen tensiones en más de una dirección. Para una determinada relación de valores, tales tensiones combinadas pueden causar la fluencia o fractura del material, aún cuando individualmente no alcancen los guarismos de falla.TEORIAS DE FALLA:La necesidad de la cuidadosa consideración de un criterio de falla es ilustrada por la sigueinte figura

8. TEORIAS DE FALLASForma general del criterio de falla:Un estado multiaxial de tensiones en un cuerpo, es el estado más general que puede presentarse ante una condición de solicitación. En la práctica, suele ser complejo y hasta a veces imposible idear experimentos que puedan cubrir cada detalle y cada particular combinación de tensiones.En la materia consideraremos dos posibilidades de falla: a) Falla para materiales Dúctiles. b) Falla para materiales Frágiles.En la aplicación de un criterio de fluencia, la resistencia del material está dado por su resistencia de fluencia. La resistencia de fluencia más comúnmente disponible es la resistencia a la tracción s0, determinada a partir de un ensayo uniaxial utilizando las deformaciones plásticas ya descriptas.

9. TEORIAS DE FALLASEn la aplicación de un criterio de fractura, se utiliza usualmente la resistencia última a la tracción su. Los criterios de fractura para materiales isotrópicos pueden ser expresados en la forma matemática siguiente:Dónde se predice que ocurre la falla (fractura o fluencia), cuando una función matemática específica, f, de las tensiones normales principales es igual a la resistencia de falla del material, sc, en un ensayode tracción uniaxial. La expresión matemática también puede ser presentada en función de componentes de tensión según un sistema de ejes cartesianos que no sea el de las tensionesprincipales.

10. TEORIAS DE FALLASCRITERIO DE FALLA DE LA MAXIMATENSION NORMAL (o Teoría de Rankine):aquel en que se espera la falla cuando la mayor de las tensiones principales alcanza la resistencia uniaxial del material. Como esta aproximación ha tenido gran suceso en la predicción de la fractura de materiales frágiles debería ser considerado como un criterio de fractura distinguiéndolo del criterio de fluencia.Elcriterio de fractura de la máxima tensión normal puede ser especificado por una función particular,f, como sigue:Representación gráfica del criterio de la máxima tensión normalPara EPT, tal que s3= 0, este criterio puede ser representado gráficamente en una gráfica de s1 versuss2 por un cuadrado

11. TEORIAS DE FALLASLas ecuaciones para las cuatro líneas rectas que forman los bordes de esta región segura son obtenidas:Para el caso general, dónde las tres tensiones principales pueden ser distintas de cero, la relación anterior indica que la región segura es la acotada por:

12. TEORIAS DE FALLASSi uno de los valores de s1, s2 o s3 es cero, entonces sólo necesita considerarse la región bidimensional formada por la intersección del cubo con el plano de las dos restantes tensiones principales. Tal intersección es mostrada para el caso de s3= 0, y el resultado es por supuesto el Cuadrado de la siguiente figura.Quehacer en casoque toque interpolar ?

13. TEORIAS DE FALLASEstablece que: “La falla ocurriráen la parte compleja cuando la energía de distorsión por volúmen unitario exceda una prueba de tensión simple en la falla”La energía de distorsión asociada con la fluencia es:Teoría de Von Mises o de energía de distorsión máxima :

14. TEORIAS DE FALLASElipse de la energía de distorsión máxima:

15. TEORIAS DE FALLASEsfuerzo efectivo de Von-Mises y Factor de seguridad:Se define como aquel esfuerzo a tensión uniaxial que generaría la misma energía de distorsión que la que se produciría por la combinación real de los esfuerzos aplicados

16. TEORIAS DE FALLASEstablece que:“La falla ocurre cuando el esfuerzo cortante máximo en una pieza excede el esfuerzo cortante en una probeta a tensión en el punto de fluencia (la mitad del límite de fluencia elástico a tensión)”.Factor de seguridadTeoría del esfuerzo cortante máximo:

17. TEORIAS DE FALLASHexágono de la teoría del esfuerzo cortante máximo:

18. TEORIAS DE FALLASEstablece que:“La falla ocurrirácuando el esfuerzo normal en la probeta llegue a cierto límite de la resistencia normal como el límite de fluencia elástico a tensión o la resistencia máxima a tensión”.Factor de seguridadTeoría del esfuerzo normal máximo:

19. TEORIAS DE FALLASCuadrado de la teoría del esfuerzo normal máximo:

20. TEORIAS DE FALLASComparación de los datos experimentales con las teorías de falla:

21. TEORIAS DE FALLASMateriales uniformes: Son los que tienen tendencia a tener una resistencia a compresión igual a la resistencia a tensión.Materiales no uniformes: son los materiales que tienen una resistencia mucho mayor a la compresión que a la tensión.Teoría Coulomb Mohr:

22. TEORIAS DE FALLASTeoría de Mohr modificada:

23. TEORIAS DE FALLASEsfuerzo efectivo Coulomb-Mohr y factor de seguridad

24. TEORIAS DE FALLASPor fatiga entendemos:“Fallo de un material por rotura como resultado de esfuerzos cíclicos repetitivos”.Mecanismo de las fallas por fatiga:La iniciación de la grietaLa propagación de la grietaLa fractura súbita causada por el crecimiento inestable de la grieta.Teorías de falla por fatiga:

25. TEORIAS DE FALLASLas cargas por fatiga pueden ser:Totalmente alternantesRepetidosFluctuantesCargas por fatiga:

26. TEORIAS DE FALLASCurvas compuestas S-N para aceros forjados y otros materialesCriterios de medición de las fallas por fatiga:

27. TEORIAS DE FALLASDiagrama Vida-Esfuerzo (S-N):

28. BIBLIOGRAFIADocumentoTeorias de fallabasadas en esfuerzosestaticos y dinamico(Adjuntado a la presentacion).TEORIAS DE FALLAS O DE COMPARACIÓN.28