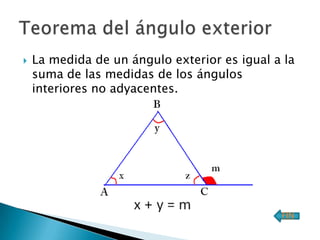
Este documento resume las propiedades fundamentales de los triángulos, incluyendo su definición, elementos, clasificación, líneas notables y teoremas fundamentales. Explica conceptos como las alturas, medianas, bisectrices y cevianas de un triángulo y los puntos donde se intersectan, como el ortocentro, baricentro e incentro. También cubre las propiedades de los ángulos interiores y exteriores de un triángulo.