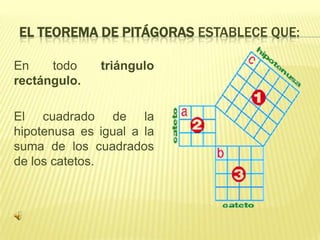
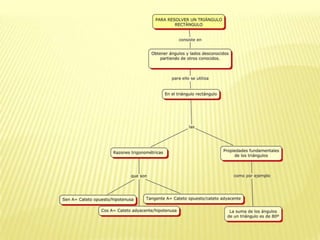
Este documento trata sobre los triángulos rectángulos. Explica que en la antigüedad civilizaciones como los mesopotamios y los egipcios ya conocían y utilizaban las propiedades de estos triángulos. Luego define los tipos de triángulos rectángulos, introduce el Teorema de Pitágoras, y muestra cómo calcular los lados desconocidos usando este teorema y las razones trigonométricas. Finalmente, plantea un problema de aplicación del teorema.

1. TRIÁNGULOS RECTÁNGULOS

2. INTRODUCCIÓN
El Teorema de Pitágoras lleva
este nombre porque su
descubrimiento recae sobre la
escuela pitagórica.
Anteriormente, en Mesopotamia
Mesopotamia
y el Antiguo Egipto se conocían
ternas de valores que se
correspondían con los lados de
un triángulo rectángulo, y se
utilizaban para resolver
problemas referentes a los
Egipto
citados triángulos, tal como se
indica en algunas tablillas y
papiros.

3. OBJETIVO
Al finalizar el alumno estará en la capacidad de:
 Definir al triángulo rectángulo.
 Identificar las figuras planas, reconociendo sus
elementos y características principales.
 Reconocer el triángulo como polígono más
importante, conociendo sus propiedades,
características y construcción.
 Clasificar los triángulos según sus lados y sus
ángulos.
 Resolver problemas matemáticos que involucren
triángulos rectángulos.

4. TRIÁNGULO RECTÁNGULO
En geometría, se
llama triángulo
rectángulo a todo
triángulo que
posee un ángulo
recto, es decir, un
ángulo de 90º
grados.

5. RECTÁNGULOS ISÓSCELES RECTÁNGULOS ESCALENOS
Triángulo rectángulo Triángulo rectángulo
isósceles. escaleno.
Un ángulo recto Un ángulo recto
Otros dos ángulos iguales de Otros dos ángulos distintos
45° No hay lados iguales
Dos lados iguales
TIPOS DE TRIÁNGULOS RECTÁNGULOS

6. TRIÁNGULO RECTÁNGULO
Se denomina
hipotenusa al lado
mayor del triángulo, el
lado opuesto al ángulo
recto. Se llaman catetos
a los dos lados menores,
los que conforman el
ángulo recto. Si la
medida de los lados son
números enteros, estos
reciben el nombre de
terna pitagórica.

7. EL TEOREMA DE PITÁGORAS ESTABLECE QUE:
En todo triángulo
rectángulo.
El cuadrado de la
hipotenusa es igual a la
suma de los cuadrados
de los catetos.

9. Fórmulas para
calcular un lado
desconocido en
función de los otros
dos, donde a y b
son los catetos y c
es la hipotenusa.

10. RAZONES TRIGONOMÉTRICAS
En un triángulo
rectángulo, las razones
trigonométricas del ángulo
α con vértice en A, son:
 El seno: la razón entre
el cateto opuesto y la
hipotenusa.
 El coseno: la razón
entre el cateto
adyacente y la
hipotenusa.
 La tangente: la razón
entre el cateto opuesto y
el adyacente,

11. PROBLEMA DE TEOREMA DE PITÁGORAS
Una escalera de incendios se
apoya en la fachada.
Evidentemente se coloca a una
distancia normalmente fijada.
Vamos a considerar que se pone
a 10 metros. Como sabes, se
puede alargar. Calcula la medida
que debe alargarse para alcanzar
un edificio de 20 m, 25m, 30m,
35m, 40m, 45m, 50m.
etc. Completa los resultados en
la tabla.
Escalera 22.36 41.23
Altura 20 25 30 35 40 45 50

12. CONCLUSIÓN
Se puede comprender un poco mejor lo que es la geometría
Euclídea; las repercusiones que ésta tuvo en pensamiento del
mundo antiguo, ya que desde la antigüedad se utilizaron las
figuras geométricas, una de ellas es el “triangulo”.
En la actualidad para un alumno el tema de “triángulos” le
servirá de base para luego conocer otras figuras de mayor
cantidad y resolver problemas de su vida cotidiana.
El estudio formal de la geometría euclidiana y de las demás
geometrías nos permite organizarlas de forma tal que
podemos conocer y entender sus estructuras conceptuales,
facilitando así su estudio.