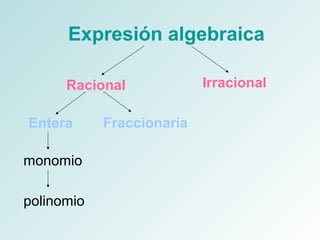
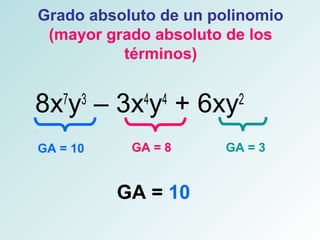
Este documento define conceptos básicos sobre polinomios como monomios, polinomios, grado relativo y absoluto. Explica que un polinomio es una expresión algebraica racional entera compuesta de uno o más monomios. También describe polinomios especiales como ordenados, completos, homogéneos e idénticamente nulos. Finalmente, incluye ejercicios de aplicación sobre estos conceptos.

1. Polinomios
Definiciones

2. Expresión algebraica
Racional Irracional
Entera Fraccionaria
monomio
polinomio

3. Polinomio
Se denomina así a una expresión
algebraica racional entera.
Ejemplos
P(x) = 3x4 +2x3 – x2 + 8x +10
Q(x;y) = 5xy3 +10x
R(x;y;z) = 2zy4 + 2x3 – xy2 + 8xz + z
Todo polinomio puede constar de
uno o más monomios

4. Monomio
Es la expresión algebraica racional en
la que se prevén solamente dos
operaciones respecto a sus variables:
multiplicación y elevación a la potencia
natural.
Ejemplos
M(x) = 3x4
Q(x;y) = 5xy3
R(x;y;z) = -xy4z2

5. NOTACIÓN DE UN POLINOMIO
Un polinomio en variable X y Y se puede
representar así:
Se lee:
“P de x e y” el cual significa:
“P” depende de x e y
Y además:
x;y Son variables
a,b,c Son constantes
m,n,p,s Son exponentes

6. Casos de Polinomios
1) 2x + 3y4
2) -4a2b – b2c
3) 6x2 - 3x + 8
4) -x2yz + 3y - 5
BINOMIOS
TRINOMIOS

7. Grados de un polinomio

8. Grado relativo con respecto a
una variable
(mayor exponente de la variable)
P(x; y; z) = 81x3 y5z6 + 20x4 yz8
GR(x)= 4 GR(y)= 5 GR(z)=8

9. Grado absoluto de un polinomio
(mayor grado absoluto de los
términos)
8x7y3 – 3x4y4 + 6xy2
GA = 10 GA = 8 GA = 3
GA = 10

10. Ejemplo 1
Si se sabe que el grado relativo a x es 5 halla:
a)El valor de m
b)El grado absoluto del polinomio
Q(x; y) =-5x4 y2 +3xm+2 y4 -4xm-1y2
Solución:

11. Ejemplo 2
Si se sabe que el grado absoluto del polinomio es 9
halla: n2 + 1
Q(x; y) =-5x4 y2 +3x3 y4 -4x2n+1y2
n + 1 =
3 +
+ =
Por lo tanto:
Solución:
2 1 2 9
2 6
3
nn
n
+ + =
=
=
2 2 1
9 1 10
n2 +1=10

12. Ejercicio 1
Si se sabe que el grado del polinomio es 11
halla: 3GR(x) - GR(y)
P(x; y) = xa+5 ya+2 + 3xa+3 y5 + 5xa ya-1
Respuesta: 17

13. Polinomios especiales

14. CONCEPTO
• Son aquellas expresiones enteras
cuyas características (grado,
coeficientes y variables) y por la
forma cómo se representan,
guardan ciertas propiedades
implícitas que las hacen notables.

15. Polinomios especiales
polinomio
ordenado
completo
homogéneo
idéntico
opuesto
nulo

16. Polinomio ordenado
x4y3 + 2x2y5 – 3xy8
3x1y8
Polinomio ordenado respecto a “x” en forma decreciente
Polinomio ordenado respecto a “y” en forma creciente.
La variable que presenta esta característica se denomina
ORDENATRIZ
Ejemplo:
P(x, y) = 6x7 y2 + 5x5 y4 - 8x3 y6 + 4y9
La variable “x” es ordenatriz decreciente de P.
La variable “y” es ordenatriz creciente de P.

17. Polinomio completo
x4y + 3x2y5 – 3x3 +xy4 – 5x0
Polinomio completo con
respecto a x.
x4y + 3x2y5 – 3x3 +xy4 – 5
Es incompleto respecto a y
x4y + 3x2y5 – 3x3 +xy4 – 5x0

18. COROLARIOS
COROLARIO 1:
En todo polinomio completo de una variable, el
número de términos es igual al grado de la
expresión aumentado en 1
Ejemplo:
P(x) = 4x + 7x3 + 5 + 6x5 + 2x2 + 8x4
# de términos = G(P) + 1
# de términos = 4 + 1=5

19. COROLARIOS
COROLARIO 2:
En todo polinomio ordenado y completo de una variable, la
diferencia de grados (en valor absoluto) de dos términos
consecutivos, es igual a la unidad:
1 ( ) ( ) 1 k k grado t grado t + - =
Ejemplo:
6 5 4 3 2
1 2 3 4 P(x) = aox + a x + a x + a x + a x + a5x + a6
1 T 2 T 3 T 4 T 5 T 6 T 7 T
3 4 grado(t ) - grado(t ) = 4 - 3 = 1

20. Polinomio homogéneo
Un polinomio de dos o más términos y
más de una variable es homogéneo, si
dichos términos presentan el mismo grado
absoluto, denominado grado de
homogeneidad
6x5y3 – 3x4y4 + 6x6y2
GA = 8 GA = 8 GA = 8
Polinomio homogéneo de grado 8

21. Polinomios idénticos
P(x) = ax3 + bx2 + c
Q(x) = 2x2 +5x3 – 8
Si P y Q son idénticos,
entonces a = 5; b = 2; c = -8
PºQ

22. Polinomio opuesto
Si P(x;y) = x4y3 + 2x2y5 – 3xy8
el polinomio opuesto de P es:
-P(x;y) = – x4y3 – 2x2y5 + 3xy8

23. Polinomio idénticamente nulo
P(x) = ax3 + bx2 - c
a = b = c = 0
P(x) º 0

24. Ejercicio 1
Si se sabe que el polinomio es completo y
ordenado en forma ascendente, calcula el
valor de 2abc. Indica el grado del
polinomio.
R(x) =p xb+2 -5xb+a+7 -2x2a+c
Respuestas:
a)2abc = 160
b)GA = 2

25. Ejercicio 2
Si se sabe que el polinomio es
idénticamente nulo, calcula el valor de
-7(a+b+c+d)
P(x) = 2d x3 + 4x2 - 6x3 + 2ax2 + 9 - 3bx + c - 12x
Respuesta: 84

26. Ejercicio 3
Si se sabe que el polinomio es homogéneo,
calcula el valor de a – b.
R(x; y) = 2x2b+1 - 6xb y7 + 2x2a+2 y
Respuesta: -1

27. PRACTICA
Calcular la suma de los valores de “n” para los cuales la
expresión es un polinomio:
n
10 -
2 128
P ( x , y ) = 4 x 2 -
3 y
2
n Para que valor o valores de “n” la expresión de las
variables “x” y “y” (n +3)xn-7 + x2 yn -(n -2) y10-n
es racional
entera.
Del polinomio: P(x, y) = 15xn+3 ym- 2 + xn+ 2 ym-3
si el GA(P) =11;
GR(x) – GR(y)=5. Hallar el valor de 2m+n.
Determinar el valor de a + b si el polinomio:
Q(x, y) = x2a+b-3 ya+b+1 + x2a+b-4 ya+b+2 + x2a+b-2 ya+b
Es de grado 28 y la diferencia de grados relativos a: x e
y sea igual a 6.

28. PRACTICA
Hallar ab(a+b) si el polinomio:
P(x, y) = xa-2b ya+b - 5xb ya+2b + xa-b y8
Es homogéneo
Determinar la suma de coeficientes si el polinomio:
Q(x) = p(xm + yn ) + m(xn + y p ) + n(xm + y p ) + mnp
Es completo y ordenado.
De un polinomio Q(x,y) completo, homogéneo de grado
8 y ordenado crecientemente respecto a x, se han
tomado tres términos consecutivos que son:
...+ xa yb+2 + M + xb ya+2 + ...
Obtener el GR(y) en el término M