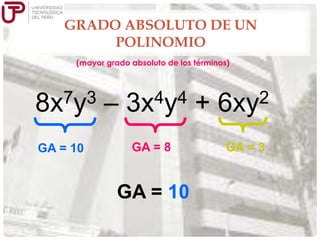
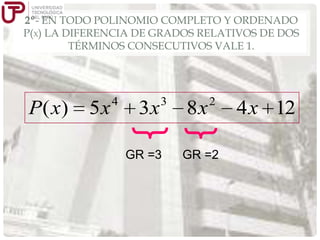
Este documento describe los conceptos básicos de los polinomios, incluyendo sus aplicaciones, definición, grados y casos especiales como polinomios ordenados, completos, homogéneos e idénticamente nulos. Explica que los polinomios son expresiones algebraicas formadas por la suma o diferencia de monomios y que su grado depende de los exponentes de las variables. Además, presenta ejemplos y ejercicios para ilustrar estas propiedades fundamentales de los polinomios.

1. NIVELACIÓN DE
MATEMÁTICA
3. TÉRMINO ALGEBRAICO Y
POLINOMIOS ESPECIALES.

2. INDICE
POLINOMIOS
-Casos, grados y clases
de un polinomio.
-Polinomios especiales
•
•
•
•
Aplicaciones
Definición
Casos de polinomios
Valor numérico
• Cambio de variable
• Grados de un polinomio
• Relativo
• Absoluto
• Polinomios especiales
• Propiedades
• Ejercicios

3. APLICACIONES
Los polinomios son una parte importante del Álgebra.
Están presentes en todos los contextos científicos y
tecnológicos: desde los ordenadores y la informática
hasta la carrera espacial.
La fórmula que expresa el movimiento
de un cuerpo en caída libre viene dada
por el siguiente polinomio:
P(t )
t: tiempo
g: gravedad
1 2
gt
2

4. DEFINICIÓN
• Un polinomio es una expresión algebraica racional
entera, es decir, los exponentes de sus variables son
números enteros positivos.
• Además, un polinomio es la suma o diferencia de
monomios.

5. POLINOMIO
Suma o diferencia de monomios
• P(x) = 3x4 +2x3 – x2 + 8x +10
• Q(x;y) = 5xy3 +10x
• R(x;y;z) = 2y4z+ 2x3 – xy2 + 8xz + z

6. CASOS DE POLINOMIOS
4
3y
1) 2x +
2) -4a2b – b2c
BINOMIOS
c
3) 6x2 - 3x + 8
4) -x2yz + 3y - 5
c
TRINOMIOS

7. VALOR NUMÉRICO
• El valor numérico de un polinomio es
el número que se obtiene al sustituir
las variables por números.

8. VALOR NUMÉRICO
•

9. CAMBIO DE VARIABLE
• El cambio de variable al igual que el
valor numérico, es el resultante de
reemplazar una variable en el
polinomio.

10. CAMBIO DE VARIABLE
•

11. GRADOS DE UN POLINOMIO

12. GRADO RELATIVO CON
RESPECTO A UNA VARIABLE
(mayor exponente de la variable)
3
5 6
P( x; y; z ) 81 x y z
4
20 x yz
8
GR(x)=4 GR(y)=5 GR(z)=8

13. GRADO ABSOLUTO DE UN
POLINOMIO
(mayor grado absoluto de los términos)
7y3
8x
GA = 10
–
4y4
3x
GA = 8
GA = 10
+
2
6xy
GA = 3

14. EJERCICIO 1
Si se sabe que el grado relativo a x es 5,calcula:
a)El valor de m
b)El grado absoluto del polinomio
Q( x; y )
Respuestas:
a) m = 3
b) GA = 9
4
5x y
2
3x
m 2
y
4
4x
m 1
y
2

15. EJERCICIO 2
Si se sabe que el grado absoluto del polinomio
es 9 halla:
n2 + 1
Q( x; y )
4
5x y
Respuesta: 10
2
3
3x y
4
4x
2n 1
y
2

16. EJERCICIO 3
Si se sabe que el grado del polinomio es 31
halla:
GR(x) + GR(y)
P( x; y )
x
a 5
Respuesta: 41
y
a 1
2a
3x y
5
a
5x y
a 2

17. POLINOMIOS ESPECIALES

18. POLINOMIOS ESPECIALES
ordenado
completo
polinomio
homogéneo
idénticos
Idénticamente
nulo

19. 1.- POLINOMIO ORDENADO
Un polinomio está ordenado cuando los
exponentes de la variable “referida” están
aumentando o disminuyendo.
Ejemplo:
9
5
P( x; y ) 6 x y 3x y
4
3 8
5x y
Ordenado en forma descendente respecto a “x”
Ordenado en forma ascendente respecto a “y”

20. EJEMPLO: POLINOMIO ORDENADO
4y
2
4y3 + 3 + 2y5y5 – 3x1y8
P(x;y)=x 2x 2x – 3xy8
x
Polinomio ordenado respecto a “x” en forma
descendente
Polinomio ordenado respecto a “y” en forma
ascendente

21. 2.- POLINOMIO COMPLETO
La variable “referida” presenta todos los
exponentes consecutivos desde 1 hasta un
mayor determinado e incluso el término
independiente.
Ejemplo:
P( x; y ) 9 x
3
4 8
7 y 4x y
2 5
x y
Completo respecto a “x” con T.I.(x)= -7y
5 xy
2

22. EJEMPLO: POLINOMIO COMPLETO
4y + 4y + y 2 5 3x 3 +xy 5x0
P(x;y)=x3x23x5y––3x3 +xy4 –4 –
x
Polinomio completo con respecto a “x”
5

23. 3.- POLINOMIO HOMOGÉNEO
Es aquel polinomio en el que todos
sus términos son del mismo grado
absoluto.
Ejemplo:
2
2 4
P( x; y; z ) 7 x y z
3 3 2
3x y z
1 7
5x y
Es un polinomio cuyo grado de homogeneidad es 8.

24. EJEMPLO:
POLINOMIO HOMOGÉNEO
P(x; y)=6x5y3 – 3x4y4 + 6x6y2
GA = 8
GA = 8
Polinomio homogéneo de grado 8
GA = 8

25. 4.- POLINOMIOS IDÉNTICOS
Dos polinomios son idénticos si verifican:
- Los dos polinomios tienen el mismo grado.
- Los coeficientes de los términos semejantes son
iguales.
9
5
P( x; y ) ax y bx y
3 8
Q( x; y) 6 x y
5
4
3x y
3 8
cx y
4
9
5x y
Se debe cumplir: a = 5; b = 3; c = 6

26. EJEMPLO:
POLINOMIOS IDÉNTICOS
3
ax
2
bx
P(x) =
+
+c
2 +5x3 – 8
Q(x) = 2x
Si P y Q son idénticos,
Entonces:
a = 5; b = 2; c = -8
P Q

27. 5.- POLINOMIO IDÉNTICAMENTE
NULO
Es aquel polinomio cuyos coeficientes de
cada uno de sus términos son ceros.
P( x; y )
Ax
3
4
Bx y
2
2
Cx y
8
Dy
Se debe cumplir: A= 0; B = 0; C = 0; D = 0
5
0

28. EJEMPLO:
POLINOMIO IDÉNTICAMENTE
NULO
P(x) =
3
ax
+
2
bx
-c
Se cumple: a = b = c = 0
P(x)
0

29. RESUMEN
Fuente: texto escolar matemática 3-hipervinculos, (2013), Perú: Santillana

30. PROPIEDADES

31. 1º- SIENDO P(X) UN POLINOMIO COMPLETO
SE CUMPLE:
de términos de P(x) = Grado de P(x) + 1
P( x) 5 x
4
3x
2
Se observa:
- Número de términos = 5
- Grado de P(x) = 4
8 4x x
3

32. 2º- EN TODO POLINOMIO COMPLETO Y ORDENADO
P(X) LA DIFERENCIA DE GRADOS RELATIVOS DE DOS
TÉRMINOS CONSECUTIVOS VALE 1.
P( x)
5x
4
3x
3
GR =3
8x
2
GR =2
4 x 12

33. EJERCICIOS

34. EJERCICIO 1
Si se sabe que el polinomio es completo y
ordenado en forma creciente, calcula el valor de
2abc. Indica el grado del polinomio.
R( x)
x
b 2
Respuestas:
a)2abc = 160
b)GA = 2
5x
b a 7
2x
2a c

35. EJERCICIO 2
Si se sabe que el polinomio es completo y
ordenado en forma decreciente, calcula el
valor de a - b - c.
P( x) x
3b c
x
a 2b
Respuesta: a-b-c= -1
x
a b c
x
c

36. EJERCICIO 3
Si se sabe que el polinomio:
P ( x ) 2d x
3
4x
2
6x
3
2ax
2
9 3bx c 12 x
es idénticamente nulo, calcula el valor de
-7(a+b+c+d)
Respuesta: 84

37. EJERCICIO 4
Si se sabe que el polinomio es homogéneo,
calcula el valor de a – b.
R( x; y )
2x
2b 1
Respuesta: -1
b
6x y
7
2x
2a 2
y

38. EJERCICIO 5
Si se sabe que el polinomio es homogéneo de
grado 7, calcula el valor de 2a – b.
P( x; y )
2x
a 1
y
2b a
Respuesta: 2a – b = 5
6x
a b
y
2a 1