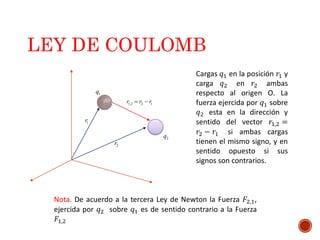
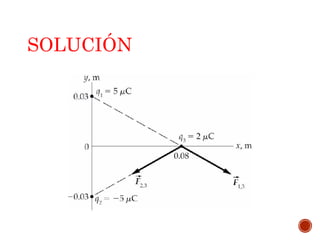
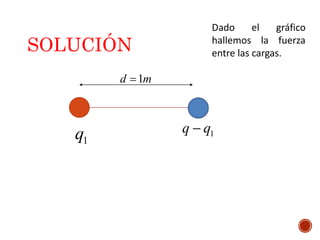
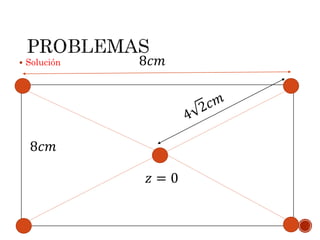
El documento discute los conceptos fundamentales de la teoría electromagnética en condiciones estáticas. Explica la ley de Coulomb, que cuantifica la fuerza entre cargas eléctricas puntuales. Define el campo eléctrico creado por un cuerpo cargado y presenta varios problemas para calcular fuerzas entre cargas usando la ley de Coulomb.