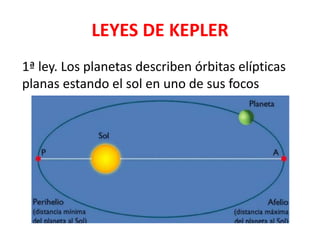
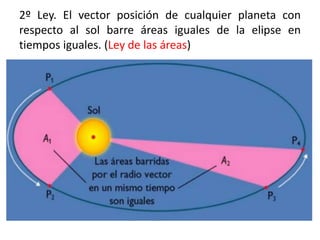
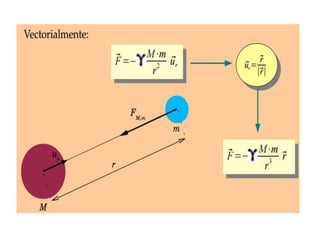
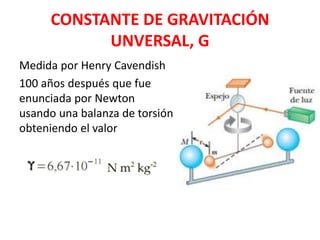
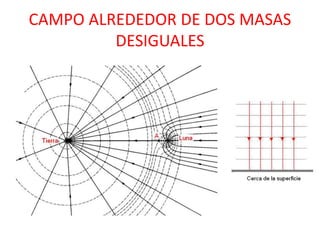
Este documento resume diferentes modelos cosmológicos como la teoría geocéntrica de Ptolomeo y la teoría heliocéntrica de Copérnico. También describe las tres leyes de Kepler sobre los movimientos planetarios y cómo Galileo y Kepler confirmaron la teoría heliocéntrica. Explica la ley de gravitación universal de Newton y conceptos como la energía potencial gravitatoria, el campo gravitatorio y las líneas de fuerza del campo.

1. UNIVERSIDAD NACIONAL DE TRUJILLO
FISICA III
UNIDAD 1: INTERACCIÓN GRAVITATORIA
Prof. Dr. Elvar Quezada Castillo

2. MODELOS COSMOLÓGICAS
• Teoría Geocéntrica: Modelo de
Ptolomeo (100 a 170 d.C.). La
tierra es el centro del universo.
En su libro El Almagesto (140
d.C.) dice: cada cuerpo describe
círculos, llamados epiciclos y
que el centro de este círculo se
desplazaba sobre otro círculo
llamado deferente.

3. MODELOS COSMOLÓGICOS
• Teoría heliocéntrica. Modelo de Copérnico
(1473-1543 d.C.). El sol es el centro del
universo. En su libro De Revolutionibus
Orbium Coelestium (1543), publicado cuando
estaba muriendo manifestaba que la tierra
tenía tres movimientos: giraba en una órbita
circular alrededor del sol, rotaba sobre un eje
inclinado y tenía un movimiento de precesión.

4. CONFIRMACIÓN DE LA TEORÍA
HELIOCÉNTRICA
• Galileo Galilei (1564 - 1642).
Publica observaciones recogidas de la observación con un
telescopio construido por él.
• Johannes Kepler (1571 -1630).
Enuncia las leyes de los movimientos planetarios basándose
en las observaciones de Tycho Brahe (1546 - 1601)

5. LEYES DE KEPLER
1ª ley. Los planetas describen órbitas elípticas
planas estando el sol en uno de sus focos

6. 2º Ley. El vector posición de cualquier planeta con
respecto al sol barre áreas iguales de la elipse en
tiempos iguales. (Ley de las áreas)

7. 3ª ley. Los cuadrados de los períodos de
revolución son proporcionales a los cubos de las
distancias promedio de los planetas al sol.
Donde T = período, k una constante y a la distancia
media

8. EL SISTEMA SOLAR
• Todos los planetas efectúan dos movimientos distintos: uno de
rotación y otro de traslación.
• Todos los planetas describen órbitas planas alrededor del Sol.
• Casi todas las órbitas planetarias están aproximadamente en el
mismo plano.
• Todos los planetas se trasladan en el mismo sentido alrededor del Sol
• El eje de rotación de la mayor parte de los planetas, salvo Urano
y Plutón es prácticamente perpendicular al plano orbital.
• La mayoría de los satélites describen órbitas en el plano ecuatorial de
los planetas.
• Todos los planetas rotan en sentido antihorario, excepto Venus,
Urano y Plutón

9. LEY DE GRAVITACIÓN UNIVERSAL
Fue enunciada por Isaac Newton en 1666 y publicada
en 1687 en su monumental obra: Philosophia Naturalis
Principia Mathematica, establece que:
La fuerza de atracción gravitacional entre dos cuerpos
es directamente proporcional al producto de las mases
e inversamente proporcional al cuadro de la distancia
que los separa.

11. LEY DE GRATITACIÓN UNIVERSAL

12. CONSTANTE DE GRAVITACIÓN
UNVERSAL, G
Medida por Henry Cavendish
100 años después que fue
enunciada por Newton
usando una balanza de torsión
obteniendo el valor

13. MASA INERCIAL Y MASA
GRAVITACIONAL
• La masa gravitatoria (mg) es la propiedad que tiene un cuerpo de atraer a
otro mediante la fuerza gravitatoria.
• La masa inercial (mi) mide la resistencia que presenta un cuerpo a cambiar
su estado de movimiento cuando se aplica una fuerza. Es decir, se resiste a
acelerarse, a mayor masa menor aceleración. Y esta masa podría depender
de la composición química del cuerpo, de su temperatura u otra variable
desconocida.
• Pues bien, aunque en principio parecen propiedades distintas,
experimentalmente la masa gravitatoria y inercial de un cuerpo son iguales:
mg = mi
• Este resultado se conoce como principio de equivalencia: Todos los cuerpos
situados en el mismo lugar en un campo gravitacional experimentan la
misma aceleración.

14. ENERGÍA POTENCIAL GRAVITACIONAL
• La fuerza gravitacional, es central, depende de la
distancia y corresponde a una fuerza conservativa.
• A esta fuerza le corresponde una energía potencial
gravitacional, dada por:
De donde

16. Integrando
Obtenemos
La energía total del sistema de dos partículas sometidas
a su interacción gravitacional es

17. Para un sistema de más de dos partículas, sometidas a su
interacción gravitacional, la energía total es
En el caso de dos partículas, refiriendo su movimiento a
un sistema de referencia situado en el centro de masa del
sistema, se expresa la energía cinética en función de la
masa reducida µ dada por

18. - Si la energía total es negativa (E<0), todas las órbitas
son elípticas (o cerradas) cuando definimos la energía
potencial como cero para una separación infinita.
Una órbita cerrada significa que la energía cinética no
es suficiente en ningún punto de la órbita para llevar la
partícula al infinito
- Si la energía es positiva (E>0), la partícula puede llegar al
infinito y tener una energía cinética, esto es:
- Si la energía es igual a cero (E = 0) de acuerdo a la ec.
anterior la partícula se encuentra en el infinito con velocidad
cero. La órbita aún esta abierta pero en lugar de ser una
hipérbola, es ahora una parábola.

19. GRÁFICA MOSTRANDO LOS TRES CASOS POSIBLES
INDICANDO EN CADA CASO, LA ENERGÍA POTENCIAL,
LA ENERGÍA CINÉTICA Y EL TIPO DE ÓRBITA

20. TRAYECTORIA DE UNA
PARTÍCULA LANZADA
HORIZONTALMENTE
DESDE UNA ALTURA h
SOBRE LA SUPERFICIE
TERRESTRE CON UNA
VELOCIDAD v0

21. Para poner en órbita un satélite que se lanza desde la
tierra hasta una altura h. Si a esa altura recibe un
impulso en el punto A con velocidad horizontal vo . La
energía total del satélite en A es:
La órbita será una elipse, una parábola o una hipérbola
dependiendo de que E sea, negativa, cero o positiva. En
todos los casos el centro de la tierra se encuentra en el
foco de la trayectoria. Si la energía es pequeña la órbita
elíptica interceptará la tierra y el satélite retornará. Si
no lo fuera se moverá en una órbita cerrada, o escapará
de la tierra, dependiendo del valor de vo.

22. CAMPO GRAVITACIONAL
¿Cual es el campo de una partícula?

23. INTENSIDAD DE CAMPO GRAVITATORIO

24. CAMPO GRAVITATORIO CREADO POR
CUERPOS ESFÉRICOS

25. SUPERPOSICIÓN DE CAMPOS GRAVITATORIOS

26. LINEAS DE FUERZA DE UN CAMPO
GRAVITACIONAL
Un campo gravitacional se representa figurativamente
por líneas de fuerza.

27. Representación gráfica del campo
gravitacional

28. CAMPO ALREDEDOR DE DOS MASAS
DESIGUALES

29. POTENCIAL GRAVITATORIO

30. RELACIONES ENTRE INTENSIDAD DE
CAMPO Y POTENCIAL

31. GRACIAS POR SU ATENCIÓN