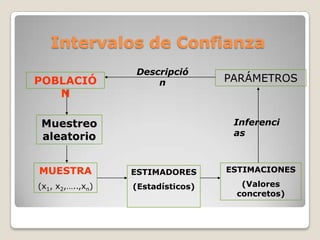
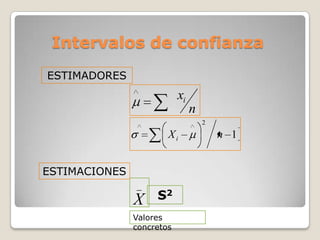
Este documento describe los intervalos de confianza y cómo se construyen. Explica que un intervalo de confianza ofrece un rango de valores que probablemente incluya el parámetro de interés de la población, como la media, con un cierto nivel de confianza. A través de un ejemplo, muestra cómo calcular un intervalo de confianza para la media y cómo su amplitud se reduce a medida que aumenta el tamaño de la muestra.

1. Estadística
Josué Gilberto Álvarez Muñiz
Carrera: Procesos industriales área manufactura
Profesor: Lic. Edgar Mata Ortiz
Materia: Estadística

2. Intervalos de Confianza
Inferencia Estadística

3. Intervalos de Confianza
Métodos de estimación:
Estimación puntual:
utilización de datos de
la muestra para
calcular un solo
número
Estimación de intervalo:

4. Intervalos de Confianza
Métodos de estimación:
Estimación Estimación de
puntual: intervalo:
utilización de datos ofrece un intervalo de
de la muestra para valores razonables
calcular un solo dentro del cual se
número para estimar pretende que esté el
el parámetro de parámetro de interés,
interés. en este caso la media
poblacional, con un
cierto grado de
confianza

5. Intervalos de Confianza
Descripció
POBLACIÓ n PARÁMETROS
N
Muestreo Inferenci
aleatorio as
MUESTRA ESTIMADORES ESTIMACIONES
(x1, x2,…..,xn) (Estadísticos) (Valores
concretos)

6. Intervalos de confianza
ESTIMADORES
xi
n
2
Xi n 1
ESTIMACIONES
_
X S2
Valores
concretos

7. Ejemplo: distribución de tallas
de neonatos
Valores desconocidos de
2 los parámetros media y
variancia de la talla de la
población
2 Estimadores
xi Xi n 1
n
Muestra
46;48;51;52;52
46 49 51 52 52 Estimación puntual de
x 50
5
2 2 Estimación puntual de
46 50 ....... 52 50
s2 6,5 2
5 1

8. Intervalos de confianza
bilaterales: construcción
Dada una variable aleatoria X con media
y desviación estándar ,
el teorema del límite central afirma que posee una
que posee
distribución normal estándar si X :
- se encuentra distribuida normalmente,
- no se encuentra distribuida normalmente y n
sea suficientemente grande
x
Z
n

9. Para una variable normal estándar, 95% de las observaciones
se ubican entre -1,96 y +1,96.
En otras palabras, la probabilidad de que Z tome un valor
entre -1,96 y +1,96 es:
P 1,96 Z 1,96 0,95
Al sustituir el valor de
Z:
x
P 1,96 1,96 0,95
/ n

10. Multiplicamos los tres términos de la
desigualdad por el error estándar
n
Por tanto,
P 1,96 x 1,96 0,95
n n

11. Restamos de cada término de tal
manera que:
P 1,96 x 1,96 x 0,95
n n
Multiplicamos por -1, invirtiendo el
sentido de la desigualdad:
P 1,96 x 1,96 x 0,95
n n

12. Al reordenar términos:
P x 1,96 x 1,96 0,95
n n
La x ya no se localiza en el centro de la
desigualdad; en lugar de eso, la afirmación
de probabilística indica algo sobre

13. Al reordenar términos:
P x 1,96 x 1,96 0,95
n n

14. Intervalos de Confianza
 Importante:
Cuando las muestras aleatorias son cada
vez más grandes, la variabilidad de X
se torna más pequeño.
Sin embargo la variabilidad inherente de
la población estudiada, medida por
, siempre se encuentra presente.

15.  Ejemplo :
Distribución de los niveles de colesterol en
sangre de todos los varones que son
hipertensos y que fuman.
◦ Esta distribución es:
 aproximadamente normal,
 con una media desconocida: = ?,
 y una desviación estándar
= 46 mg / 100 ml.

16.  Interesa calcular el nivel medio de
colesterol en sangre.
 Antes de elegir una muestra aleatoria, la
probabilidad de que el intervalo
contenga la verdadera media poblacional
es de = 0,95. 46 46
( X 1.96 , X 1.96 )
n n)

17. Intervalos de Confianza
 En el caso de tomar una muestra
tamaño 12 de la población de
fumadores hipertensos y que además
poseen un nivel medio de colesterol en
sangre de x = 217 mg / 100 ml.
 El intervalo de confianza es de 95%
para es
46 46
( 217 1.96 ,217 1.96 )
12 12
o
(191,243)

18.  Este intervalo contiene el valor de 211 mg
/100 ml, el nivel medio de colesterol en la
sangre de todos los hombres de 20 a 74
años de edad sin importar si son
hipertensos o fumadores.
Se está 95 % seguro de que los límites 191
y 243 cubren la verdadera media .
Interpretació
n1

19. Interpretación 2: en términos de frecuencia.
Si se tomaran 100 muestras aleatorias de
tamaño 12 de esta población y utilizaran cada
muestra para construir un intervalo de
confianza de 95 %, se espera que en promedio
95 de los intervalos cubrieran la verdadera
media poblacional = 211 y 5 no.

20. Intervalos de Confianza
Este
procedimiento se
expresa
gráficamente de
la siguiente
forma:

21. Intervalos de Confianza
Interpretación del gráfico:
 La única cantidad que varia de muestra es X.
 Todos tiene la misma amplitud.
 Cada intervalo de confianza que no contenga
el valor verdadero de se encuentra marcado
con un punto, 5 intervalos están dentro de
esta categoría

22. Intervalos de Confianza
Para calcular un intervalo de
confianza
de 99% para .
Con la misma muestra de 12 hipertensos, se
encuentra que los límites son
46 46
(217 2.58 ,217 2.58 )
12 12
o
(183,251)

23. Interpretación:
 Un 99% de confianza de este intervalo cubre el
verdadero nivel medio de colesterol en sangre de
la población.
 La amplitud de intervalo de confianza de 99% es
de 251-183=68 mg/ 100 ml.
 Este intervalo es más amplio que el
correspondiente intervalo de confianza de 95%.

24. Intervalos de Confianza
Reflexionando en el sentido del
tamaño muestral:
¿Qué dimensiones debe tener una
muestra para que la amplitud del
intervalo se reduzca a solo 20 mg/100
ml?

25. Consideraciones:
Ya que el intervalo se centra en la media
de muestreo x=217 mg/ 100 ml, interesa
el tamaño de la muestra necesario para
generar el intervalo (217-10, 217+10)
ó
(207, 227)

26.  Para determinar el tamaño n que se
requiere de la muestra, se debe resolver
la ecuación
2.58(46)
10
10
n 140.8

27.  Se necesita una muestra de 141 hombres
para reducir la amplitud del intervalo de
confianza de 99% a 20 mg/100 ml.
 Aunque la media de muestreo de 217
mg/100 ml se ubica en el centro del
intervalo, no desempeña ningún papel en
la determinación de su amplitud; la
amplitud es función de , n y el nivel de
confianza.