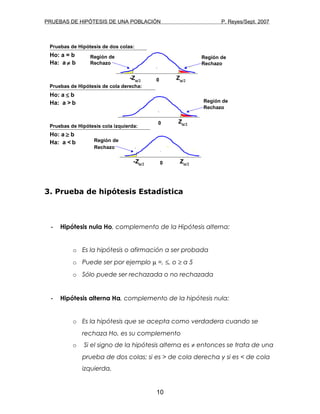
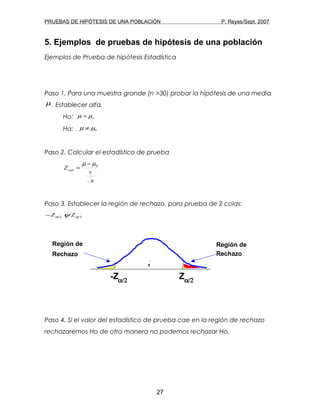
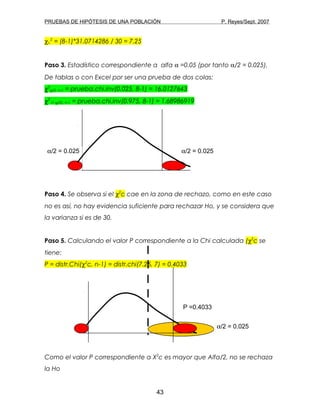
Este documento describe las pruebas de hipótesis para una población. Explica los elementos clave de una prueba de hipótesis como la hipótesis nula, la hipótesis alternativa, el estadístico de prueba y las regiones de rechazo. También detalla los pasos para realizar una prueba de hipótesis y los tipos de pruebas como de dos colas, de cola derecha y de cola izquierda.