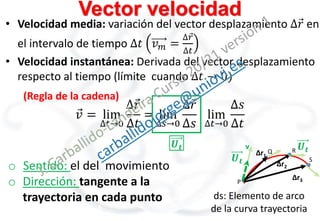
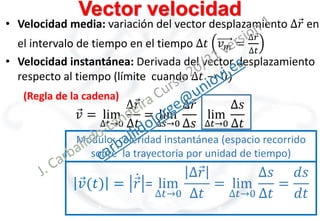
El documento trata sobre la cinemática de la partícula. Explica conceptos como sistema de referencia, vector de posición, velocidad, aceleración y sus componentes. Describe movimientos particulares como el movimiento rectilíneo uniforme y uniformemente acelerado. También cubre la composición de movimientos, ilustrando esto con un ejemplo de movimiento parabólico.