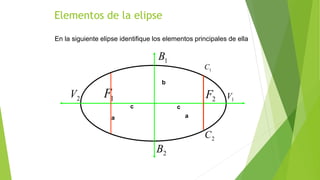
La elipse es un lugar geométrico de puntos donde la suma de las distancias a dos puntos fijos, llamados focos, es constante. Sus elementos principales incluyen focos, vértices, y los ejes mayor y menor, con ecuaciones canónicas que dependen de la orientación del eje mayor. Se detallan métodos para obtener la forma canónica de la elipse a partir de su ecuación general y cómo identificar sus características.

1. LA ELIPSE
Estefanía Cruz

2. LA ELIPSE
La elipse es el lugar geométrico de todos los puntos P(x,y) cuya ubicación en el
plano es tal que , la suma de sus distancias a dos puntos fijos de él es constante.
Estos dos puntos fijos del plano, se llaman FOCOS y se designan por y
1F 2FP(x,y)
X
Y
O
1F 2F
1V 2V
1 2( , ) ( , ) tand P F d P F cons te 

3. Elementos de la elipse
 Los elementos más importantes de la elipse son:
 FOCOS: Los puntos fijos
 RECTA FOCAL: La recta a la que pertenecen los
focos
 RECTA SECUNDARIA: La simetral del segmento
 CENTRO: Punto de intersección de las rectas focal y
secundaria y que equidista de los focos .
 VÉRTICES : Puntos de intersección de la elipse con la
recta focal. Se designan:
1 2F yF
1 2VV
1 2B B 1 2FF
1 2V yV

4. • EJE MAYOR: Segmento que se considera de longitud 2 a: a es el
valor del semieje mayor .
• EJE MENOR: Segmento de la recta secundaria interceptada por la elipse
. Se considera de longitud 2b : b es el valor del semieje menor.
• DISTANCIA FOCAL: Medida del segmento
Se considera de longitud 2c.
LADO RECTO : Cuerda focal perpendicular a la recta focal o eje de simetría
. Su medida es
1 2VV
1 2B B
1 2FF
1 2C C
2
2b
a

5. Elementos de la elipse
1B
2B
1V2V 1F 2F
1C
2C
a a
c c
b
En la siguiente elipse identifique los elementos principales de ella

6. Ecuación canónica de la elipse
con centro (0,0)

7.  La ecuación canónica de la elipse con eje mayor sobre el eje X y centro en ( 0, 0) es:
 La ecuación canónica de la elipse con eje mayor sobre el eje Y y centro en ( 0, 0) es:
12
2
2
2

b
y
a
x
( a > b )
12
2
2
2

b
y
a
x
( a < b )

8.  Ejemplo1.
 Analizar la ecuación 4x2 + y2 + 24x – 6y + 29 = 0, encontrar:
 Los valores de a, b, y c
 La ecuación del lado recto
 Coordenadas de los vértices
 Coordenadas de los focos
 Solución
 Llevamos la ecuación a la forma canónica 4x2 + y2 + 24x – 6y + 29 = 0
1
)()(
2
2
2
2




b
ky
a
hx
así:

9.  Asociamos en un paréntesis los términos en x y en otro los términos en y pasando al otro miembro
el término independiente ( 4x2 + 24x + ) + ( y2 – 6y + ) = – 29
 Factorizamos cada paréntesis de tal forma que el coeficiente del término al cuadrado sea uno así:
4(x2 + 6x + ) + ( y2 – 6y + ) = – 29
 Formamos en cada paréntesis un trinomio cuadrado perfecto sumando en cada paréntesis el
cuadrado de la mitad del coeficiente del segundo término de cada paréntesis y este mismo valor lo
sumamos en el segundo miembro de la ecuación multiplicada por el coeficiente de cada paréntesis
así: 4[x2+ 6x +(3)2 ] + [y2 – 6y + (3)2] = – 29 + 4(3)2 + (3)2.
 Factorizamos los paréntesis que son trinomios cuadrados perfectos y efectuamos el segundo
miembro así:
4(x + 3 )2 + ( y – 3)2 = – 29 + 4( 9 ) + 9
4(x + 3 )2 + ( y – 3)2 = – 20 + 36
4(x + 3 )2 + ( y – 3)2 = 16 ahora llevamos la ecuación a la forma
dividiendo cada término de la ecuación por el segundo miembro así
1
)()(
2
2
2
2




b
ky
a
hx

10. entonces la ecuación queda después de simplificar :
Por lo tanto:
𝑏 = 16 = 4 𝑐 = 𝑏2 + 𝑎2 = 16 − 4 = 12 = 2 3
Por lo tanto a = 2 ; b = 4 ; c = 23 y el eje mayor es paralelo al eje Y ya que a < b.
La longitud del lado recto es 2x = 2a2/b
2x = 2( 2 )2 / 4
2x = 2
x = 1
16
16
16
)3(
16
)3(4 22



 yx
1
16
)3(
4
)3( 22



 yx
𝑎 = 4 = 2

11.  Las coordenadas de los vértices son; V1 = ( h , k – b ); V2 = ( h , k + b ); donde h = – 3; k = 3; b =
4 entonces V1 = ( –3, 3 – 4) ; V2 =(–3, 3+ 4 ) V1 = ( – 3 , – 1) ; V2 = ( – 3 , 7 )
 Las coordenadas de los focos son: F1 = ( h , k – c ) ; F2 = ( h ,k + c ) donde h = – 3 ; k = 3 ; c
= 2 3 : luego F1 = (– 3 , 3 – 2 3 ) ; F2 = (– 3, 3 + 2 3 )
 Grafica de la ecuación 4x2 + y2 + 24x – 6y + 29 = 0 de C = ( h , k) es:

12. Ecuación de la elipse con centro en (h , k)
Para hallar la ecuación canónica de una elipse con centro en C( h , k) se
deben considerar dos casos: cuando el eje focal es paralelo al eje x y cuando
es paralelo al eje y.
Ecuación canónica de la elipse con centro en (h,k) y eje focal paralelo al eje x

13. Elementos de la elipse son:
Centro: (ℎ . 𝑘 )
Focos: 𝐹₁(ℎ − 𝑥, 𝑘) y 𝐹₂(ℎ + 𝑐, 𝑘)
Vértices: 𝑉₁(ℎ + 𝑎, 𝑘) y 𝑉2 ℎ + a, k
Puntos de corte en el eje normal:𝐵₁(ℎ, 𝑘 − 𝑏) y 𝐵₂(ℎ, 𝑘 + 𝑏)
Longitud del lado mayor: 2a
Longitud del lado menor: 2b
Eje focal: 𝑦 = 𝑘
Longitud del lado recto:
2𝑏²
𝑎
La ecuación canónica cuando tiene centro (h , k) y eje focal paralelo al
eje x es:
(𝑥−ℎ)²
𝑎²
+
(𝑦−𝑘)²
𝑏²
= 1, donde a > b > 0 y a²= b² + c²

14. Cuando una elipse tiene centro C(h,k) y eje focal paralelo al eje y, sus elementos
quedan definidos de la siguiente forma:
Centro: (ℎ , 𝑘 )
Focos: 𝐹₁(ℎ, 𝑘 − 𝑐) y 𝐹₂(ℎ, 𝑘 + 𝑐)
Vértices: 𝑉₁(ℎ, 𝑘 − 𝑎) y 𝑉2 ℎ, k + c
Puntos de corte en el eje normal:𝐵₁(ℎ − 𝑏, 𝑘) y 𝐵₂(ℎ + 𝑏, 𝑘)
Longitud del lado mayor: 2a
Longitud del lado menor: 2b
Eje focal: 𝑥 = ℎ
Longitud del lado recto:
2𝑏²
𝑎
La ecuación de la elipse con centro C(h,k) y eje focal paralelo al eje y es:
(𝑥−ℎ)²
𝑏²
+
(𝑦−𝑘)²
𝑎²
= 1, donde a > b > 0 y a²= b² + c²

15. Ecuación general de la elipse
 La elipse tiene una ecuación
general de segundo grado.
 No es necesario conocer si el eje
focal es paralelo al eje x o al eje y.
 Si D=E=0, entonces el centro de la
elipse es el origen del plano
cartesiano.
 Con A y B, diferentes de cero y con
el mismo signo.