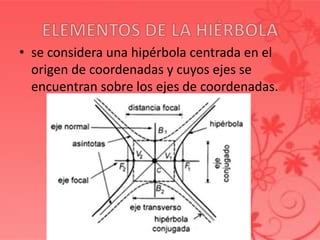
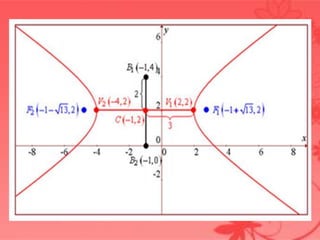
El documento describe los elementos básicos de una hipérbola, incluyendo sus focos, vértices, ejes (focal, transverso, normal y conjugado) y asintotas. También presenta las ecuaciones canónicas de una hipérbola con el centro en el origen o fuera del origen, y provee ejemplos para encontrar los elementos de una hipérbola dada y graficarla.

2. INTEGRANTES:
Adriana Borja
Angie Gamero
Andrea De la Rosa

3. • Es el lugar geométrico de los puntos del plano
tales que la diferencia de sus distancias a dos
puntos fijos, llamados focos.

4. • se considera una hipérbola centrada en el
origen de coordenadas y cuyos ejes se
encuentran sobre los ejes de coordenadas.

5. • LOS FOCOS: Son dos puntos fijos del
plano.
• EL EJE FOCAL: es la recta que pasa por
los focos.
• Los focos y el eje focal siempre están
juntos en el mismo eje
• LOS VERTICES: son los puntos en los
cuales la hipérbola corta el eje focal
• EL EJE TRANSVERSO: es el segmento que
tiene por extremos los vértices de la
hipérbola.

6. • EL CENTRO: es el punto medio del eje
transverso también puede estar dentro del
origen y fuera del origen. Siempre esta en
medio de los vértices y los focos
• EL EJE NORMAL: es la recta que pasa por el
centro y es perpendicular al eje focal.
• EL EJE CONJUGADO: es el segmento
perpendicular al eje transverso, en el centro.
El eje conjugado esta contenido en el eje
normal.
• LAS ASINTOTAS: Son dos rectas a las cuales se
aproximan las ramas de la hipérbola, al
extenderse infinitivamente.

7. • La hipérbola con centro (0,0)y focos en f1
(-c,0) y f2 (c,0) tal que la diferencia de las
distancia de un punto p (x,y)de la
hipérbola a los focos es 2ª, tienen por
ecuación canónica, la expresión:
•
𝑥2
𝑎2 -
𝑦2
𝑏2= 1
Donde a,b,c > o,c> a y 𝑏2
=𝑐2
- 𝑎2
•
𝑦2
𝑎2 -
𝑥2
𝑏2= 1
Donde a,b,c >o c >a y 𝑏2
= 𝑐2
- 𝑎2

8. • Ejemplo:
Encuentra cada uno de los elementos de la siguiente
hipérbola y grafícala:
Es una hipérbola con centro en el origen y como el
primer término contiene a , ésta es una hipérbola con
eje focal sobre el eje x, entonces se trata de una
ecuación del tipo .

9. Coordenadas del centro
Semidistancia focal
y
Coordenadas de los focos y y
Coordenadas de los
vértices
y
y
Coordenadas de los
extremos del eje conjugado
y
y
Semieje transverso
Semieje conjugado

11. • EJEMPLO:
Los focos y los vértices de una hipérbola son los
puntos: , , y , respectivamente.
Determina la ecuación de la hipérbola.
SOLUCION:
Podemos notar que el centro de la hipérbola es
el origen y además el eje focal es paralelo al eje
y, ya que las abscisas de cada uno de los puntos
son las mismas.

12. • La ecuación de la hipérbola con centro en el origen y
eje focal paralelo al eje y es Busquemos los
datos que no conocemos.
Como y entonces
A=1
Además, como y
entonces
c=3
El único dato que nos falta es para calcularlo
utilizamos la expresión , ya que tenemos
los valores de c=3 y a =1

13. Para determinar la ecuación, sustituimos los
valores a=1 y en entonces

14. • La hipérbola con centro en (h,k), focos
f1(h-c,k) y f2 (h+c,k)tal que la diferencia de las
distancias de cualquier punto P(x,y) de la
hipérbola, a los focos es 2a, tiene por
ecuación canónica:
(𝑥−ℎ)2
𝑎2 -
(𝑦−𝑘)2
𝑏2 =1, con c > a y 𝑏2
=𝑐2
-𝑎2

15. • Los elementos de la hipérbola con centro fuera
del origen (h,k) y eje focal al eje x
• Focos: 𝑓1(h-c,k) 𝑓2(h+c,k)
• Vértices: 𝑣1(h-a,k) 𝑣2(h+a,k)
• Longitud del eje transverso: 2a
• Longitud del eje conjugado: 2b
• Eje normal: paralelo al eje y
• Asíntotas: y-k=
𝑏
𝑎
(x-h)
y-k=-
𝑏
𝑎
(x-h)

16. • Ejemplo:
Encuentra cada uno de los elementos de la
siguiente hipérbola y grafícala:
Solucion:
Es una hipérbola con centro fuera del origen y
como el primer término contiene a , ésta es una
elipse con eje focal paralelo al eje x, entonces se
trata de una ecuación del tipo

17. Coordenad
as del centro
y
Semidistan
cia focal
y
Coordenad
as de los
focos
y y
Coordenad
as de
los vérti
ces
y y
Coordenad
as de los
extremos del
eje
conjugado
y
y
Semieje
transverso
Semieje
conjugado

19. 1.Encuentra cada uno de los elementos de la
siguiente hipérbola y grafícala:
2.Determina la ecuación de la hipérbola usando
los siguientes datos: el centro está en el origen,
vértice en y el extremo del eje conjugado
es .