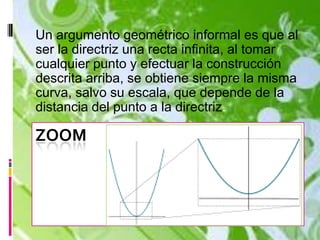
La parábola es un lugar geométrico formado por puntos que cumplen la misma distancia a un foco y una directriz. Tiene elementos como el vértice, la distancia focal y el lado recto, y todas las parábolas son semejantes en forma, variando solo en escala. Su aplicación práctica se encuentra en antenas satelitales y cocinas solares, aprovechando su capacidad para concentrar señales y radiación en un punto específico.

1. GEOMETRÍA ANALÍTICA
PARABOLA
CETis 162 Álvaro
Obregón

2. Integrantes del equipo
 NUÑO PÉREZ GERALDINE
 LOMELÍ MENDOZA ROCÍO
 MÁRQUEZ PÉREZ SURISADAI
 MENDOZA TAMAYO IVETTE
3G

3. DEFINICION
La parábola, como lugar geométrico, se forma por
una infinidad de puntos que cumplen la siguiente
condición: su distancia a un punto fijo llamado
foco y a una recta llamada directriz es la misma.
*Si el plano es paralelo a
una recta generatriz y que
corta todas las demás, su
intercesión da lugar a una
parábola

4. ELEMENTOS DE UNA PARABOLA
 Foco: es el punto fijo (p,0) y se encuentra a
una distancia p del vértice.
 Vértice: es el punto de intersección de la
parábola con su eje principal (eje de simetría
que divide dos partes iguales).
 Parámetro: p representa la distancia del foco
al vértice o de este a la directriz.
 Directriz: recta fija que se encuentra a una
distancia p del vértice de la parábola.

5. INSTRUCCIONES PARA HACER UNA
PARÁBOLA
De esta forma, una vez fija una recta y un punto
se puede construir una parábola que los tenga por
foco y directriz de acuerdo a la siguiente
construcción. Sea T un punto cualquiera de la recta
directriz. Se une con el foco dado F y a continuación
se traza la mediatriz (o perpendicular por el punto
medio) del segmento TF. La intersección de la
mediatriz con la perpendicular por T a la directriz da
como resultado un punto P que pertenece a la
parábola. Repitiendo el proceso para diferentes
puntos T se puede aproximar tantos puntos de la
parábola como sea necesario

6. Los puntos de la
Construcción de
parábola están a la
misma distancia del foco puntos en una
F y de la recta directriz. parábola.
DISTANCIA FOCAL  DIRECTRIZ

7. Lado recto
De la construcción se puede
probar que la parábola es EJEMPLO
simétrica respecto a la línea
perpendicular a la directriz y que
pasa por el foco. Al punto de
intersección de la parábola con
tal línea (conocida como eje de la
parábola) se le conoce como
vértice de la parábola y es el
punto cuya distancia a la
directriz es mínima. La distancia
entre el vértice y el foco se
conoce como distancia focal o
radio focal.

8.  Al segmento de recta
comprendido por la
parábola, que pasa por el
foco y es paralelo a la
directriz, se le conoce como
lado recto.
 La longitud del lado recto es
siempre 4 veces la distancia
focal.

9.  Siendo D, E los extremos del lado recto y T, U
las respectivas proyecciones sobre la
directriz, denotando por W la proyección del
foco F sobre la directriz, se observa que FEUW
y DFWT son cuadrados, y sus lados miden
FW=2FV. Por tanto el segmento DE es igual a
4 veces el segmento FV (la distancia focal).

10.  Las tangentes a la parábola que pasan por los
extremos del lado recto forman ángulos de 45°
con el mismo. Además, tales tangentes se
cortan en la directriz de forma perpendicular,
propiedades que pueden ser aprovechadas
para construir una aproximación geométrica
del foco y la directriz cuando éstos son
desconocidos.

11. Semejanza de todas las
parábolas
 Todas las parábolas son semejantes, es únicamente la
escala la que crea la apariencia de que tienen formas
diferentes.
 Dado que la parábola es una sección cónica, también
puede describirse como la única sección cónica que tiene
excentricidad e = 1. La unicidad se refiere a que todas las
parábolas son semejantes, es decir, tienen la misma
forma, salvo su escala.
 Al estudiar analíticamente las parábolas (basándose en
ecuaciones), se suele afirmar erróneamente que los
parámetros de la ecuación cambian la forma de la
parábola, haciéndola más ancha o estrecha. La verdad es
que todas las parábolas tienen la misma forma, pero la
escala (zoom) crea la ilusión de que hay parábolas de
formas diferentes.

12. Un argumento geométrico informal es que al
ser la directriz una recta infinita, al tomar
cualquier punto y efectuar la construcción
descrita arriba, se obtiene siempre la misma
curva, salvo su escala, que depende de la
distancia del punto a la directriz.
ZOOM

13. ECUACIONES DE LA PARABOLA
Vértice Eje focal Focos Ecuación ordinaria Grafica
Origen Horizontal F(c,0) Y2 = 4ax
C(0,0) Eje X F (-c,0) Y2=-4ax
Origen Vertical F(0,c) X2 = 4ay
C(0,0) EjeY F (0,-c) X2=-4ªy

14. Fuera del Horizontal (h + c,k) (y-k)2 =4a (x-h)
origen Eje X (h-c,k) (y-k)2= -4a(x-h)
C(h,k)
Fuera del Vertical (h, k+c) (x-h)2=4a(y-k)
origen EjeY (h, k-c) (x-h)2=-4a(y-k)
C(h,k)

15. Aplicaciones prácticas
 Una consecuencia de gran importancia es que la
tangente refleja los rayos paralelos al eje de la
parábola en dirección al foco. Las aplicaciones
prácticas son muchas: las antenas satelitales y
radiotelescopios aprovechan el principio
concentrando señales recibidas desde un emisor
lejano en un receptor colocado en la posición del
foco.
 La concentración de la radiación solar en un
punto, mediante un reflector parabólico tiene su
aplicación en pequeñas cocinas solares y grandes
centrales captadoras de energía solar.

16. APLICACIONES DE LA PARABOLA
EN LA VIDA COTIDIANA
La parábola
refleja sobre el
foco los rayos
paralelos al eje.
Análogamente,
un emisor
situado en el
foco, enviará un
haz de rayos
paralelos al eje.

17. Los
radiotelescopios
concentran los
haces de señales
en un receptor
situado en el
foco. El mismo
principio se
aplica en una
antena de radar.

18. Cocina solar
de
concentrador
parabólico. El
mismo
método se
emplea en las
grandes
centrales
captadoras de
energía solar.

19. Los faros de
los
automóviles
envían haces
de luz
paralelos, si
la bombilla
se sitúa en el
foco de una
superficie
parabólica

20.  http://www.youtube.com/watch?v=_YOPO4
mtl_s
 http://www.youtube.com/watch?v=mNDsgH
SmFFU&feature=relmfu
 http://www.youtube.com/watch?v=dl0Gmtx6
U-E&feature=fvwrel
 http://www.youtube.com/watch?v=D1GYBN
R_9Z8
 http://www.youtube.com/watch?feature=end
screen&NR=1&v=335OvX_AhjY

21. BIBLIOGRAFIA
 http://es.wikipedia.org/wiki/Par%C3%A1bola_(matem
%C3%A1tica)#Aplicaciones_pr.C3.A1cticas
 VIDEOS: youtube.com/ asesoría de matematicas.com
 Benjamín Garza, Matemáticas III G.A. Edición 1991
 Benjamín Garza, Matemáticas III G.A Edición 2000
 Landaverde, Curso de Geometría, sexta edición 1977
 Israel Sánchez, G.A. con enfoque por competencias
 Matemáticas 3, editorial esfinge
Noviembre-Diciembre 2011