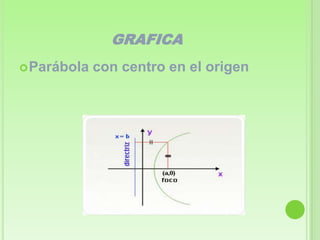
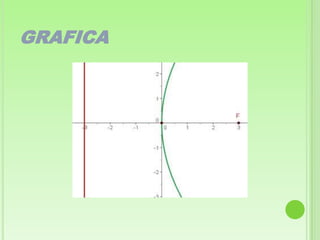
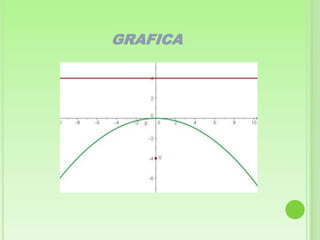
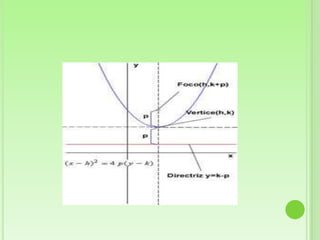
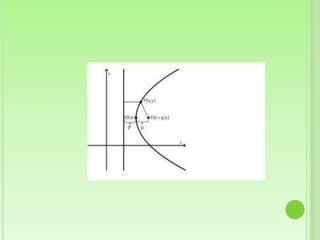
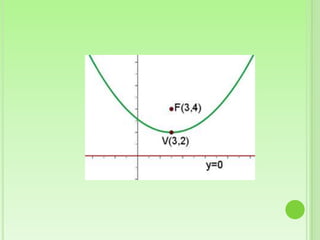
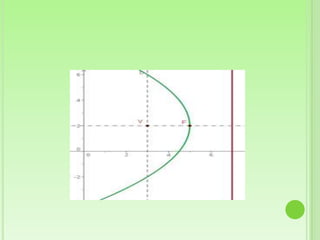
Este documento define la parábola geométricamente como el conjunto de puntos equidistantes de un foco y una directriz. Explica los elementos clave de una parábola, incluido el foco, directriz, eje y lado recto. Luego proporciona las ecuaciones canónicas de parábolas con el vértice en el origen y cómo obtener las ecuaciones cuando el vértice no está en el origen. Finalmente, presenta ejemplos para ilustrar cómo calcular los elementos de una parábola dada y encontrar su ecuación.

1. LA
PARÁBOLA

2. OBJETIVO
Al finalizar la clase los alumnos/as
serán capaces de:
Identificar los elementos que
componen la parábola, así como las
diversas ecuaciones que toma dicha
gráfica de acuerdo a su dirección.

3. DEFINICION
Se llama parábola al conjunto de
puntos del plano que equidistan de
un punto fijo, llamado foco, y una
recta fija, llamada directriz.

4. GRAFICA
 Parábola con centro en el origen

5. ELEMENTOS DE LA PARÁBOLA.
 Directriz:
es la recta que equidista
de todos los puntos de la parábola
con el foco.
 Foco: es el punto fijo que equidista
de todos los puntos de la parábola
y la directriz.

6.  Eje
de la parábola: es la recta que
contiene al vértice y al foco.
 Lado recto: es el segmento de
recta perpendicular al eje de la
parábola, que pasa por el foco y su
longitud es cuatro veces la
distancia del vértice al foco.

7. ECUACIONES CANÓNICAS DE LA PARÁBOLA
CON VÉRTICE EN EL ORIGEN

8. EJEMPLO 1
Determina la ecuación de la
parábola que tiene:
De directriz x = -3, de foco (3, 0).

9. GRAFICA

10. EJEMPLO 2
Determine la ecuación de la
parábola que tienen:
De directriz y = 4, de vértice (0, 0).

11. GRAFICA

12.  Cuándo el vértice no está en el origen,
la ecuación se obtienen mediante una
traslación.
 Si
la parábola es vertical hacia arriba
se tiene un vértice en (h, k) y el foco
en (h, k+p).

14. PARÁBOLA HORIZONTAL CON VÉRTICE
FUERA DEL ORIGEN
 Para la parábola horizontal se
intercambia x con y, el vértice es en
(h, k) y el foco en
(h+p, k).

16. EJEMPLO 1
Dada la parábola
calcular su vértice, su foco y la
recta de la directriz

18. EJEMPLO 2
Encuentre la ecuación de la
parábola de foco (3, 2), de vértice
(5, 2).

20. .
FINALMENTE LA ECUACIÓN GENERAL DE LA
PARÁBOLA ES.

21. POR SU ATENCIÓN
PRESTADA GRACIAS