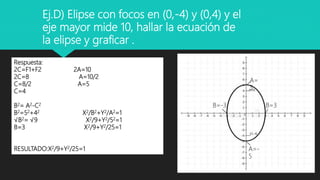
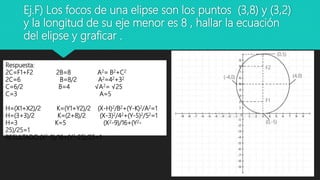
El documento ofrece una explicación detallada sobre el concepto de elipse y sus elementos, incluyendo definiciones y ecuaciones canónicas para diferentes orientaciones. Se presentan ejercicios resueltos que aplican estas ecuaciones para calcular la forma y graficar diversas elipses. Además, se discute la ecuación general de la elipse y se resuelve un ejercicio utilizando esta forma.

1. Profesor: Miguel Gerdez
Integrantes :
*Hengys Ascanio #04
*Daniel Rodríguez #38
*Marco Torrealba #42
Año y sección: 5to año “B”
Republica bolivariana de Venezuela
Ministerio del poder popular para la educación
U.E Colegio “Del Santísimo”
Barquisimeto , Estado Lara
Mayo,2018

2. A) Definición de Elipse como lugar geométrico.
Es el lugar
geométrico de
todos los puntos de
un plano, tales que
la suma de las
distancias a otros
dos puntos fijos
llamados focos es
constante.

3. B)Elementos de una Elipse (construir gráfica).
1. Focos: Son los puntos fijos F y F'.
2. Eje focal: Es la recta que pasa por los focos.
3. Eje secundario: Es la mediatriz del segmento FF'.
4. Centro: Es el punto de intersección de los ejes.
5. Radios vectores: Son los segmentos que van desde un punto de la elipse a
los focos: PF y PF'.
6. Distancia focal: Es el segmento de longitud 2c, c es el valor de la
semidistancia focal.
7. Vértices: Son los puntos de intersección de la elipse con los ejes: A, A', B y B'.
8. Eje mayor: Es el segmento segmento de longitud 2a, a es el valor del semieje
mayor.
9. Eje menor: Es el segmento segmento de longitud 2b, b es el valor del
semieje menor.
10. Ejes de simetría: Son las rectas que contienen al eje mayor o al eje menor.
11. Centro de simetría: Coincide con el centro de la elipse, que es el punto de
intersección de los ejes de simetría.

4. C) Ecuación canónica de la Elipse con vértice
en (0,0) y eje focal sobre el eje “x”.
La ecuación de una elipse de centro en el
origen , eje focal el eje X , distancia focal
igual a 2C y cantidad constante igual a 2A
es “X2/B2 +Y2/A2 =1”

5. D)Ecuación canónica de la Elipse con vértice en
(0,0) y eje focal sobre el eje “y”.
Si el eje de la elipse coincide con el eje
Y de manera que las coordenadas de
los focos sea (0,-C) Y (0,C), la ecuación
de la elipse es “X2/A2 + Y2/B2 =1”

6. E) Ecuación canónica de la Elipse con vértice en
(h,k) y eje focal paralelo al eje “x”.
La ecuación de la elipse de centro el
punto (H,K) y el eje focal paralelo al
eje X , esta dada por la segunda
forma ordinaria
“(X-H)2/A2 + (Y-K)2/B2 = 1”

7. F) Ecuación canónica de la Elipse con vértice en
(h,k) y eje focal paralelo al eje “y”.
Si el eje focal es paralelo al eje Y , su
ecuación esta dada por la segunda
forma ordinaria “(X-H)2/B2 +
(Y-K)2/A2 =1”

8. Ejercicios resueltos donde se utilizan las
ecuaciones canónicas de la Elipse (uno de la c,
uno de la d, uno de la e y uno de la f).
Ej.c) Elipse con focos en (-3,0) y (3,0) y el eje menor
mide 4, hallar la ecuación de la elipse y graficar .
Respuesta:
2C=F1+F2 2B=4
2C=6 B=4/2
C=6/2 B=2
C=3
A2= B2+C2
A2=22+32 X2/A2+Y2/B2=1
√A2= √13 X2/13+Y2/22=1
A=3,6 X2/13+Y2/4=1
RESULTADO:X2/13+Y2/4=1
(A=3,6)(A=-3,6)
(-3,0) (3,0)
B=2
B=2

9. Respuesta:
2C=F1+F2 2A=10
2C=8 A=10/2
C=8/2 A=5
C=4
B2= A2-C2
B2=52+42 X2/B2+Y2/A2=1
√B2= √9 X2/9+Y2/52=1
B=3 X2/9+Y2/25=1
RESULTADO:X2/9+Y2/25=1
A=
5
B=3
A=-
5
B=-3
(O,-4)
(O,4)
Ej.D) Elipse con focos en (0,-4) y (0,4) y el
eje mayor mide 10, hallar la ecuación de
la elipse y graficar .

10. Respuesta:
2C=F1+F2 2A=8 B2= A2-C2
2C=6 A=8/2 B2=42-32
C=6/2 A=4 √B2= √7
C=3 B=2,6
H=(X1+X2)/2 K=(Y1+Y2)/2 (X-H)2/A2+(Y-K)2/B2=1
H=(4+2)/2 K=(3+3)/2 (X-3)2/42+(Y-3)2/2,62=1
H=3 K=3 (X2-9)/16+(Y2-9)/7=1
RESULTADO:(X2-9)/16+(Y2-9)/7=1
A=4
F1 F2
B=(0,2.6)
A=(-4,0)
F1 F2
B=(0,-2.6)
A=(4,0)
Ej.E) Los focos de una elipse son los puntos
(4,3) y (2,3) y la longitud de su eje mayor es 8 ,
hallar la ecuación del elipse y graficar .

11. Ej.F) Los focos de una elipse son los puntos (3,8) y (3,2)
y la longitud de su eje menor es 8 , hallar la ecuación
del elipse y graficar .
F2
F1
(0,5)
(4,0)
(0,-5)
(-4,0)
Respuesta:
2C=F1+F2 2B=8 A2= B2+C2
2C=6 B=8/2 A2=42+32
C=6/2 B=4 √A2= √25
C=3 A=5
H=(X1+X2)/2 K=(Y1+Y2)/2 (X-H)2/B2+(Y-K)2/A2=1
H=(3+3)/2 K=(2+8)/2 (X-3)2/42+(Y-5)2/52=1
H=3 K=5 (X2-9)/16+(Y2-
25)/25=1
RESULTADO:(X2-9)/16+(Y2-25)/25=1

12. Ecuación general de la Elipse.
Si los coeficientes A y C con del mismo
signo la ecuación
“Ax2 +Cy2+Dx +Ey +F=0” representa una
elipse de ejes paralelos a las coordenadas
o bien un punto o no representa ningún
lugar geométrico real.

13. i) Ejercicio resuelto donde se utilice la ecuación
general de la Elipse.
Hallar la ecuación general de la elipse cuyo centro (2,-1) su eje focal es paralelo X y su ejes mayor y
menor miden 10 y 6 respectivamente .
Datos:
C=(2,-1) (h,k) (X-H)2/A2+(Y-K)2/B2 = 1
2A=10 --- A =10/---A=5 (X-2)2/52+(Y-1)2/32 = 1
2B=6---B=6/2---B=3 X2 – 2X * 2 +22 /25+Y2 – 2Y * 1 +12 /9 = 1
(X2 – 4X+4)/25+ (Y2 – 2Y + 1)/9 = 1
( 9(X2 – 4X +4)+25(Y2+2Y+1) )/225=1
(9X2 – 36X+36)+(25Y2 – 50Y +25)=1
9X2 +25Y2- 36X+50Y+61=225
9X2 +25Y2- 36X+50Y+61-225=0
9X2 +25Y2- 36X+50Y-164=0
RESULTADO:9X2 +25Y2- 36X+50Y-164=0