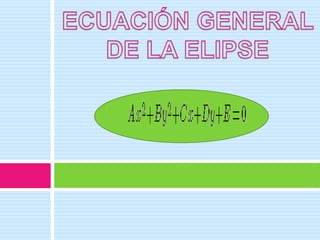
Este documento describe las características de una elipse. Define una elipse como el conjunto de puntos cuya suma de distancias a dos puntos fijos, llamados focos, es constante. Explica los elementos de una elipse como el eje principal, vértices, ejes mayor y menor, centro y lado recto. Luego presenta ejemplos de ecuaciones de elipses y resuelve problemas relacionados con encontrar los elementos de una elipse dada su ecuación.

1. INTEGRANTES:
MARÍA V MENDOZA#26
DECLAN RUIZ#40
ALEJANDRA UZTÁRIZ#44
PROFESOR:
MIGUEL GERDEZ
AÑO Y SECCIÓN:
5TO “B”

2. Una elipse es el conjunto de todos los
puntos en el plano tales que la suma de sus
distancias a dos puntos fijos F1 y F2 es
constante. Esos dos puntos fijos son los
focos de la elipse.

3. En la elipse se distinguen los siguientes elementos: eje principal o eje focal,
vértices, eje mayor, centro, eje normal o eje secundario, eje menor y lado
recto:
Eje
principal
o eje
focal:
Es la recta
que
contiene
los dos
focos.
Los
vértices:
V1 y V2
son los
puntos de
intersecció
n de la
elipse con
el eje focal.
El eje normal o
secundario:
Es la recta perpendicular
al eje focal que pasa por
el centro de la elipse.
El eje menor:
B1B2 es el
segmento que
une los puntos
de
intersección
de la elipse
con el eje
normal.
El lado recto:
Es el segmento
perpendicular
al eje focal que
pasa por el
foco y cuyos
extremos
pertenecen a la
elipse.
El eje
mayor:
V1V2 es
el
segmento
que une
los dos
vértices.
El centro
C:
Es el
punto
medio del
eje
mayor.

4. Para trazarla calcularemos las intersecciones, es decir los vértices de los
ejes menor y mayor así como los demás elementos.
Vértices eje mayor= V(0,a) y V’(0-a)
V(0,10) y V’(0-10)
Vértices eje menor= A(-b,0) y A’(b,0)
A(-6,0) y A’(6,0)
Lado recto=
Directrices=

5. Elipse con vértice en (0,0) y eje focal
sobre el eje “x”.
Elipse con vértice en (h,k) y eje focal
paralelo al
eje “x”.
Elipse con vértice en (0,0) y eje
focal sobre el eje “y”.
Elipse con vértice en (h,k) y eje
focal paralelo al eje “y”.
De la misma manera que para las
elipses con centro (0,0),
la ecuación canónica nos permite
hallar las longitudes
del semieje mayor a y del semieje
menor b.

6. 1)Encontrar la ecuación canónica de una elipse con focos F1:(4,0), F2:(-40,0) si los
vértices determinados por el eje menor son (9, ) y V2: (0,- )
Solución:
Sabemos que si los focos están situados sobre el eje x, la ecuación canónica es de la
forma tenemos que ubicar para completar la ecuación:
=7+16=23 por tanto es decir, los vértices son V1 ( ) y V2: (- )
Luego: la ecuación canónica es
2)Vemos que el semieje menor está situado sobre el eje x y en consecuencia la
ecuación será de la forma
Además, los focos están sobre el eje y están dados por y los focos son
Luego: la ecuación pedida es
y los focos son

7. 3)Analizar la ecuación 4x2 + y2 + 24x – 6y + 29 = 0, encontrar:
a.)Los valores de a, b, y c
b.)La ecuación del lado recto
c.)Coordenadas de los vértices
d.)Coordenadas de los focos
Solución
a.)Llevamos la ecuación a la forma canónica 4x2 + y2 + 24x – 6y + 29 = 0
así:
•Asociamos en un paréntesis los términos en x y en otro los términos en y pasando al otro
miembro el término independiente ( 4x2 + 24x + ) + ( y2 – 6y + ) = – 29
•Factorizamos cada paréntesis de tal forma que el coeficiente del término al cuadrado sea
uno así: 4(x2 + 6x + ) + ( y2 – 6y + ) = – 29
•Formamos en cada paréntesis un trinomio cuadrado perfecto sumando en cada paréntesis
el cuadrado de la mitad del coeficiente del segundo término de cada paréntesis y este
mismo valor lo sumamos en el segundo miembro de la ecuación multiplicada por el
coeficiente de cada paréntesis así: 4[x2+ 6x +(3)2 ] + [y2 – 6y + (3)2] = – 29 + 4(3)2 + (3)2.
•Factorizamos los paréntesis que son trinomios cuadrados perfectos y efectuamos el
segundo miembro así: 4(x + 3 )2 + ( y – 3)2 = – 29 + 4( 9 ) + 9
4(x + 3 )2 + ( y – 3)2 = – 20 + 36
4(x + 3 )2 + ( y – 3)2 = 16
ahora llevamos la ecuación a la forma

8. Dividiendo cada término de la ecuación por el segundo miembro así;
; entonces la ecuación queda después de simplificar .
Por lo tanto = 2 ; b = = 4 y = = 2
Por lo tanto a = 2 ; b = 4 ; c = 2 y el eje mayor es paralelo al eje Y ya que a < b.
b.)La longitud del lado recto es 2x = 2a2/b
2x = 2( 2 )2 / 4
2x = 2
x = 1
c.)Las coordenadas de los vértices son; V1 = ( h , k – b ); V2 = ( h , k + b );
donde h = – 3; k = 3; b = 4 entonces V1 = ( –3, 3 – 4) ; V2
=(–3, 3+ 4 ) V1 = ( – 3 , – 1) ; V2 = ( – 3 , 7 )
d.)Las coordenadas de los focos son: F1 = ( h , k – c ) ; F2 = ( h , k + c ) donde
h = – 3 ; k = 3 ; c = 2 : luego F1 = (– 3 , 3 – 2 3 ) ; F2 = (– 3, 3 + 2 )
e.)Grafica de la ecuación 4x2 + y2 + 24x – 6y + 29 = 0 de C = ( h , k) es
3

9. Dada la ecuación , encontrar:
a) Coordenadas del centro
b) Coordenadas de los vértices
Solución:
a) De la ecuación podemos concluir que y
Luego: el centro de la elipse es
b) Como 9 > 4, concluimos que , ya que a representa el semieje mayor
y b el semieje menor.
Por tanto, .Es decir, la distancia del centro a los vértices mayores es 3 y
la distancia del centro a los vértices menores es 2
Luego:
•Los vértices menores son:
•Los vértices mayores son:
4)

11. Hallar la ecuación de la elipse cuyos vértices mayores son (5,3) y (17,3) y las coordenadas
de un foco son (8,3).
Solución:
Para hallar el centro calculamos el punto medio del segmento que une los vértices del eje
mayor
Así el centro de la elipse es el punto (11,3).
Como el foco esta a 3 unidades del centro, es decir, y la distancia del centro a los
vértices es de 6 unidades, es decir . Entonces
Luego: La ecuación de la elipse es: