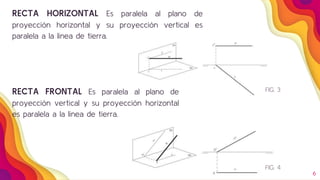
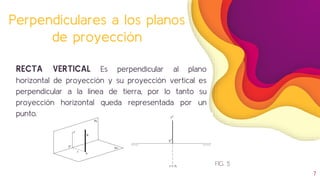
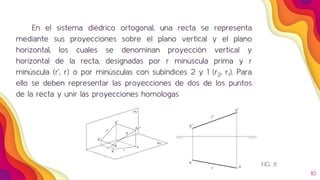
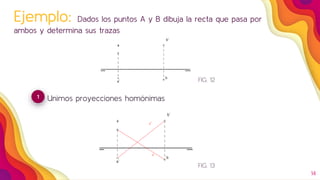
Este documento describe los diferentes tipos de rectas en el sistema diédrico ortogonal y cómo se representan y determinan sus características. Explica que una recta se define como una sucesión de puntos y que dos puntos determinan una recta. Luego detalla los diferentes tipos de rectas según si son paralelas o perpendiculares a los planos de proyección, y cómo se representan y calculan sus trazas y ángulo con los planos de proyección. Finalmente, explica cómo determinar la longitud verdadera de una recta.

1. República Bolivariana de Venezuela
Ministerio del Poder Popular para la Educación
Instituto Universitario Politécnico “Santiago Mariño”
Extensión Mérida
LA RECTA Y SUS TIPOS
Autora: Anil Alexandra Rivas Álvarez
C.I 29.520.632
Arquitectura 41
Mérida, Venezuela

2. 2
¿Qué es una línea recta? La respuesta es
sencilla y la sabemos, aunque nos cuesta
trabajo definirla nos es mas fácil trazarla sin
embargo para los matemáticos la recta es la
sucesión de puntos en una misma dirección, a
su vez, en geometría analítica podemos
encontrar que «La recta es el lugar geométrico
de los puntos tales que, tomados dos
cualesquiera del lugar geométrico, el valor de la
pendiente siempre resulta constante». A
continuación conoceremos mas sobre un punto
muy importante en geometría: la recta y sus
tipos.

3. Una recta se refiere a una sucesión de putos, a su vez dos
puntos determinan una recta, la cual se representa mediante sus
proyecciones sobre el plano vertical y horizontal, denominadas
proyección vertical y proyección horizontal de la recta.
3
¿Qué es una línea recta?
FIG. 1

4. 4
TIPOS DE
RECTAS

5. 5
Paralelas a los planos de
proyección
RECTA PARALELA A LA LINEA DE TIERRA
Sus proyecciones son paralelas a la línea de tierra.
FIG. 2

6. 6
RECTA FRONTAL Es paralela al plano de
proyección vertical y su proyección horizontal
es paralela a la línea de tierra.
RECTA HORIZONTAL Es paralela al plano de
proyección horizontal y su proyección vertical es
paralela a la línea de tierra.
FIG. 3
FIG. 4

7. 7
Perpendiculares a los planos
de proyección
RECTA VERTICAL Es perpendicular al plano
horizontal de proyección y su proyección vertical es
perpendicular a la línea de tierra, por lo tanto su
proyección horizontal queda representada por un
punto.
FIG. 5

8. 8
RECTA DE PUNTA Es perpendicular al plano vertical
de proyección y su proyección horizontal es
perpendicular a la línea de tierra, por lo tanto su
proyección vertical queda representada por un punto.
RECTA DE PERFIL Presenta sus
proyecciones normales a la línea de tierra por
pertenecer a un plano de perfil.
FIG. 6
FIG. 7

9. 9
REPRESENTACIÓN
DE LA RECTA EN
EL SDO Y TRAZAS
DE LA RECTA

10. En el sistema diédrico ortogonal, una recta se representa
mediante sus proyecciones sobre el plano vertical y el plano
horizontal, los cuales se denominan proyección vertical y
horizontal de la recta, designadas por r minúscula prima y r
minúscula (r’, r) o por minúsculas con subíndices 2 y 1 (r2, r1). Para
ello se deben representar las proyecciones de dos de los puntos
de la recta y unir las proyecciones homologas
10
FIG. 8

11. Se conocen como trazas de la recta a los puntos de
intersección de esta con los planos de proyección horizontal,
vertical y de perfil, a su vez, como cualquier otro punto, las
trazas de la recta son representadas por sus proyecciones
horizontales y verticales.
TRAZA HORIZONTAL DE UNA RECTA Es la intersección de la
recta con el plano horizontal de proyección, designada con
hache mayúscula (H) y como cualquier otro punto tiene
proyección vertical (h’) y proyección horizontal (h), esta ultima
coincide con la verdadera traza.
TRAZA VERTICAL DE UNA RECTA Se entiende por la
intersección de la recta con el plano vertical de proyección,
designada con uve mayúscula (V) y como cualquier otro
punto tiene proyección vertical (v’) coincidente con la
verdadera traza y la proyección horizontal (v).
11

12. 12
RECTA CONTENIDA EN UN BISECTOR
Sus proyecciones forman un mismo ángulo con la línea de tierra
y en la figura se representa una contenida en el primer bisector
y primer diedro.
FIG. 9

13. 13
Una vez conocidas las trazas de la recta se pueden dibujar
las proyecciones horizontal y vertical de la misma, y a su vez
se puede dar en el caso inverso, conocidas sus proyecciones,
calcular las trazas.
FIG. 10
FIG. 11

14. 14
Ejemplo: Dados los puntos A y B dibuja la recta que pasa por
ambos y determina sus trazas
1 Unimos proyecciones homónimas
FIG. 12
FIG. 13

15. Determinamos partes vistas y ocultas de la recta, nos fijamos en
la posición de las trazas de la recta
15
3
Determinamos trazas2
Vr en r’
Hr en r
Vr por encima de L.T.
implica que la vemos.
Hr por encima implica
que no la vemos.
FIG. 14
FIG. 15

16. 16
ÁNGULO DE LA
RECTA EN EL
PLANO DE
PROYECCIÓN

17. La determinación del Angulo que forma una recta con los
planos de proyección, sigue el proceso siguiente en el caso del
ángulo con el PH:
17
Se abate la traza vertical Vr, respecto de la proyección horizontal
de la recta r, para eso:
1
Por Vr se dibuja una línea perpendicular a la proyección horizontal
r1.
2
Se lleva sobre la perpendicular anterior la cota de la traza
vertical, haciendo centro en Vr1 y con radio Vr1Vr2.
3
El ángulo con el PH es el obtenido en el vértice Hr1 del triangulo
rectángulo Hr1Vr1Vr0.
4

18. Determinación del ángulo que forma la recta r con los planos de
proyección.
18
FIG. 16

19. 19
VERDADERA
LONGITUD DE LA
RECTA

20. 20
Una línea tiene una longitud definida, la cual
se determina por sus extremos, a su vez la
vista del extremo de una línea, corresponde a
un punto que representa todos los puntos de la
misma según la posición que tenga la recta con
respecto a los planos principales de proyección,
y se pueden clasificar de la siguiente manera:
1. Línea Horizontal
2. Línea Frontal
3. Línea de perfil
4. Línea vertical
5. Línea inclinada
6. Línea oblicua

21. 21
Cualquier línea en el
espacio que sea paralela a
un plano, su imagen será
proyectada sobre este plano
en su longitud verdadera, a
su vez si una línea es
paralela a una línea de
referencia en una vista,
aparecerá en su longitud
verdadera al otro lado de la
línea de referencia
FIG. 16

22. 22
Pasos a seguir para obtener la
longitud verdadera
Proyectar un plano auxiliar, paralelo a la línea en cualquier vista.1
Trazar las líneas de proyección perpendiculares a la línea de giro.2
Tomar las medidas dejando una vista intermedia del punto a la
línea de giro y transportar a el plano auxiliar.
3
La línea que se proyecta en el plano auxiliar a la dirección de
una oblicua se observara en su verdadera longitud

23. 23
FIG. 17

24. 24
La geometría descriptiva es de mucha
importancia ya que ayuda a profundizar en
aquellos aspectos que nos ayudan a
comprender la tercera dimensión, Se basa
principalmente en el manejo de conceptos tan
fundamentales de localización y espacialidad,
como lo son las determinaciones de
orientación, pendientes, verdaderas longitudes,
formas y menores distancias entre puntos o
elementos, brindándonos la posibilidad de
adquirir estos conocimientos que nos ayudaran
a entender mejor los conceptos que
manejaremos a lo largo de la carrera y en la
vida profesional en el futuro

25. ANEXOS
25
1 2 3

26. ● Sistema Diédrico. La recta. DIBUJOTECNI.COM
https://dibujotecni.com/sistema-diedrico/sistema-diedrico-la-
recta/#:~:text=Se%20denominan%20Trazas%20de%20la,sus%20proye
cciones%20horizontales%20y%20verticales.
● Sistema Diédrico. BEUNICOOS:
https://www.beunicoos.com/dibujo/sistema-diedrico
26
BIBLIOGRAFíA

27. 27
Gracias!
Por su atención