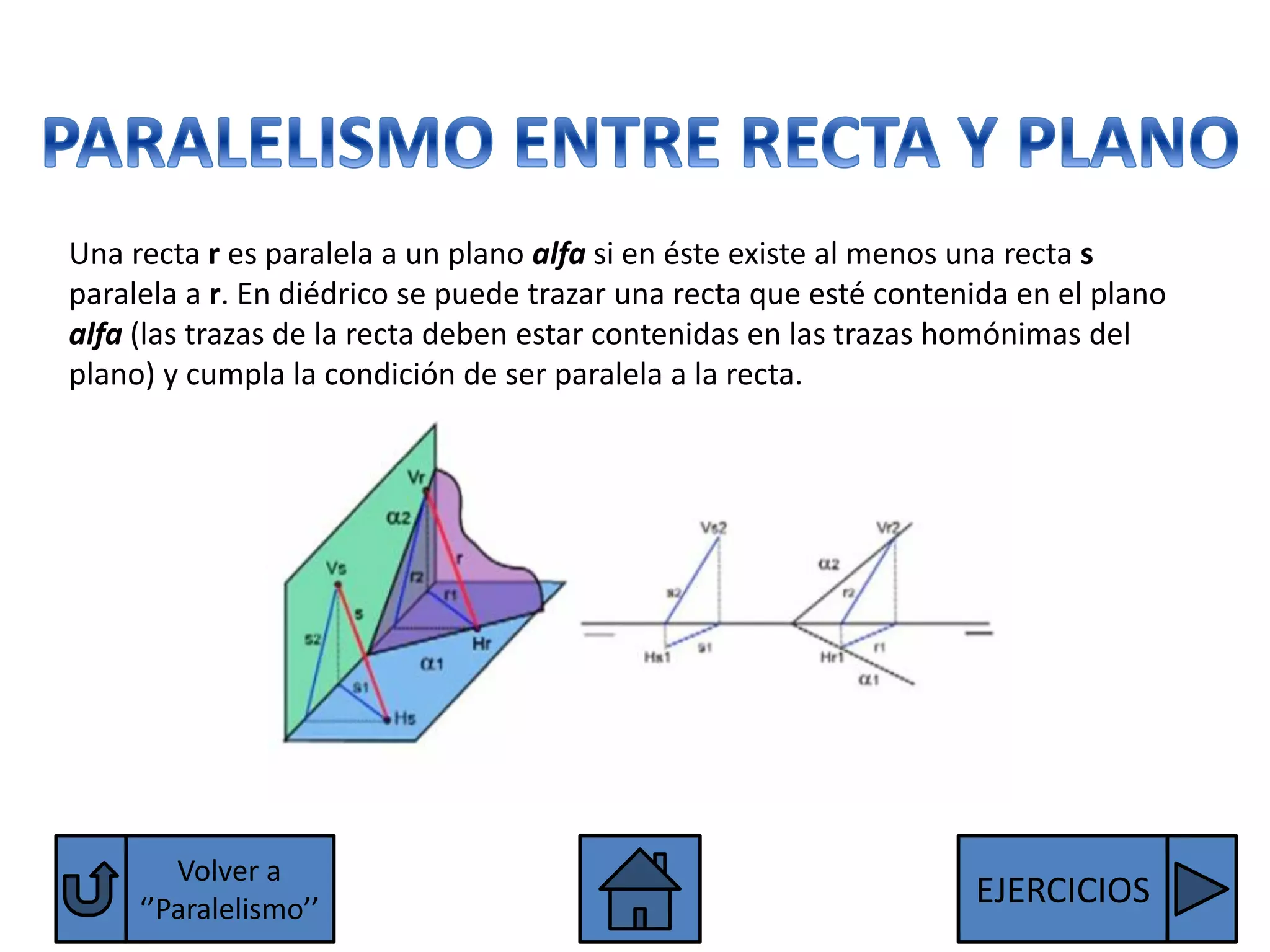
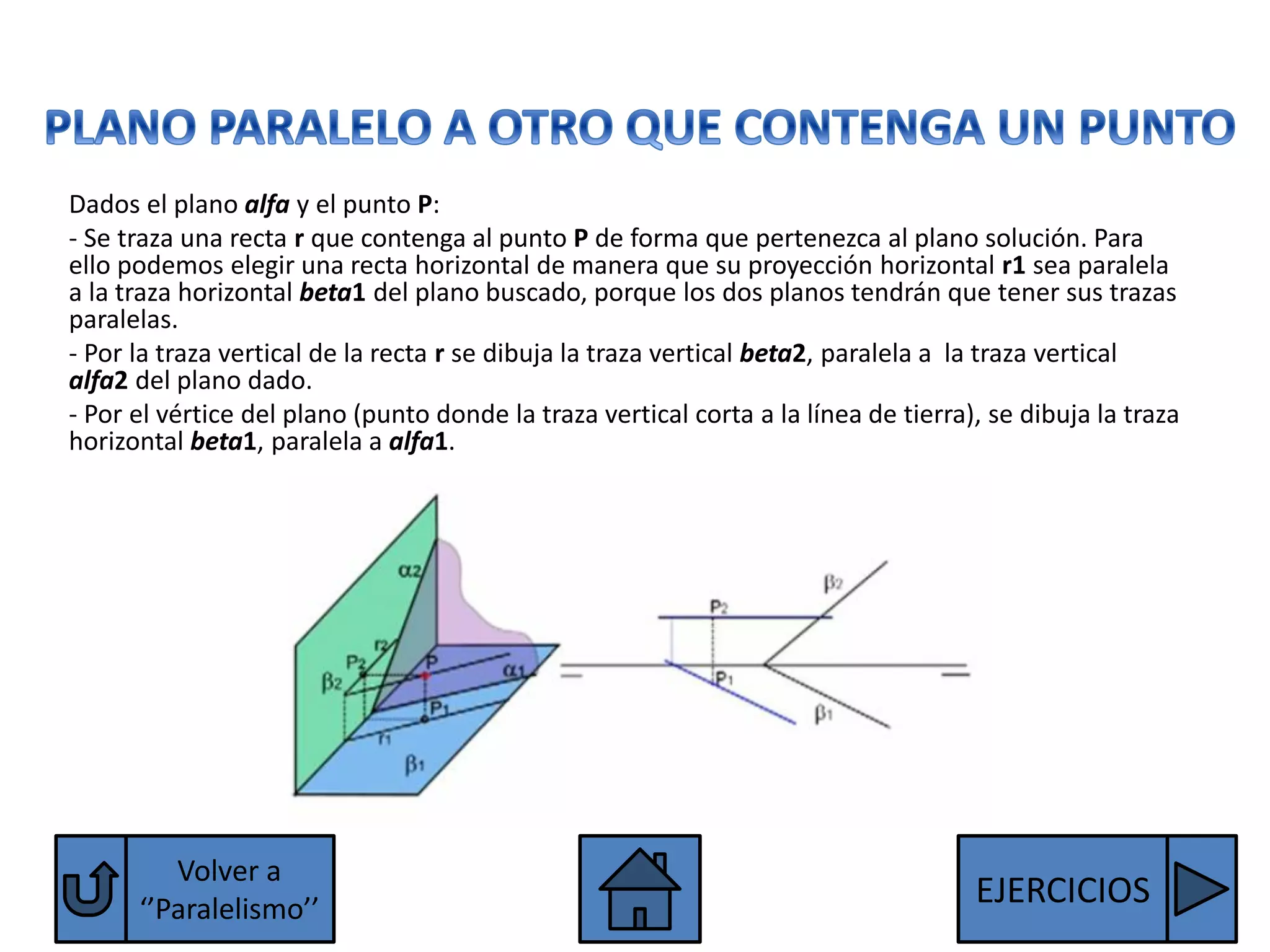
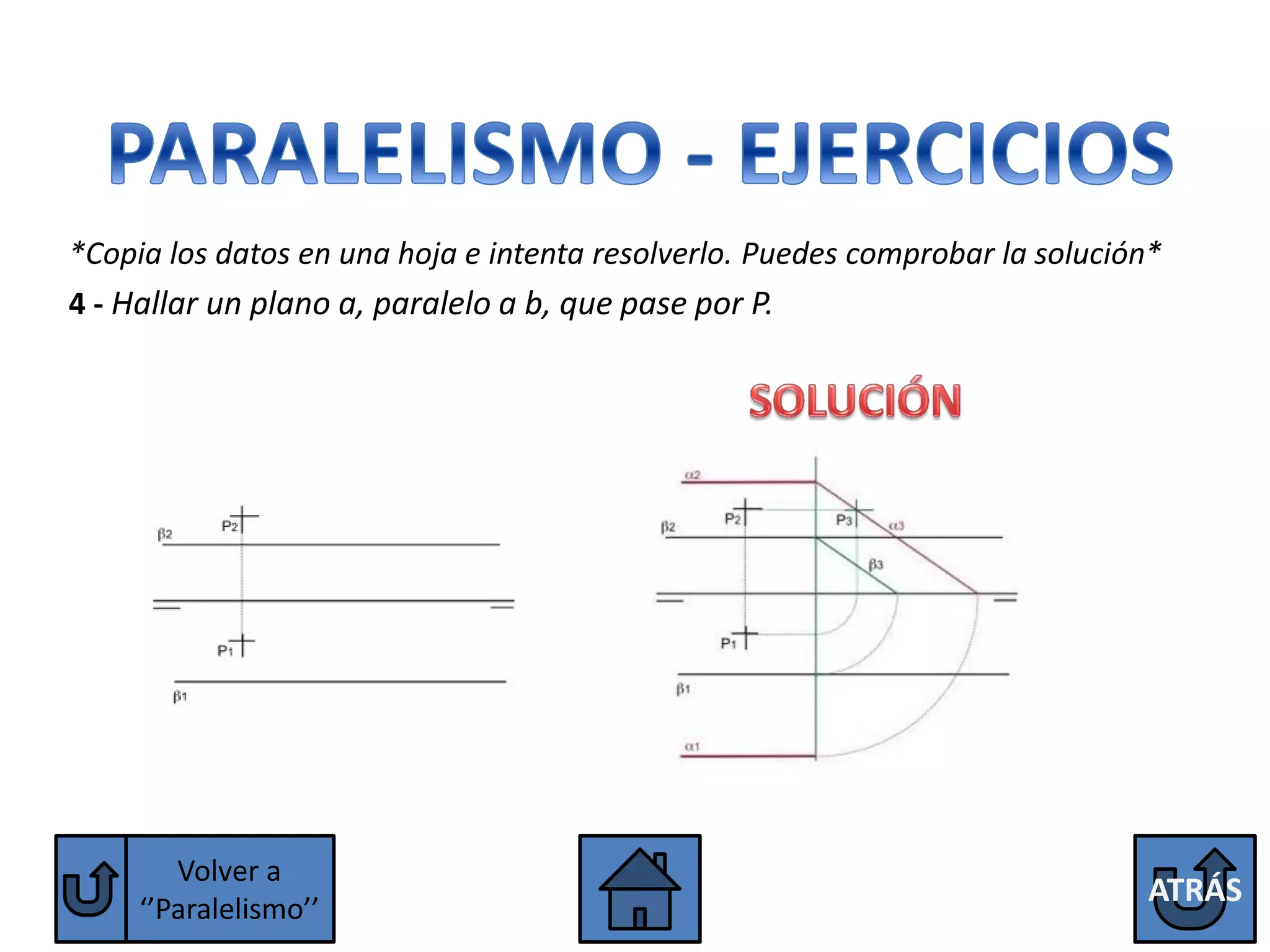
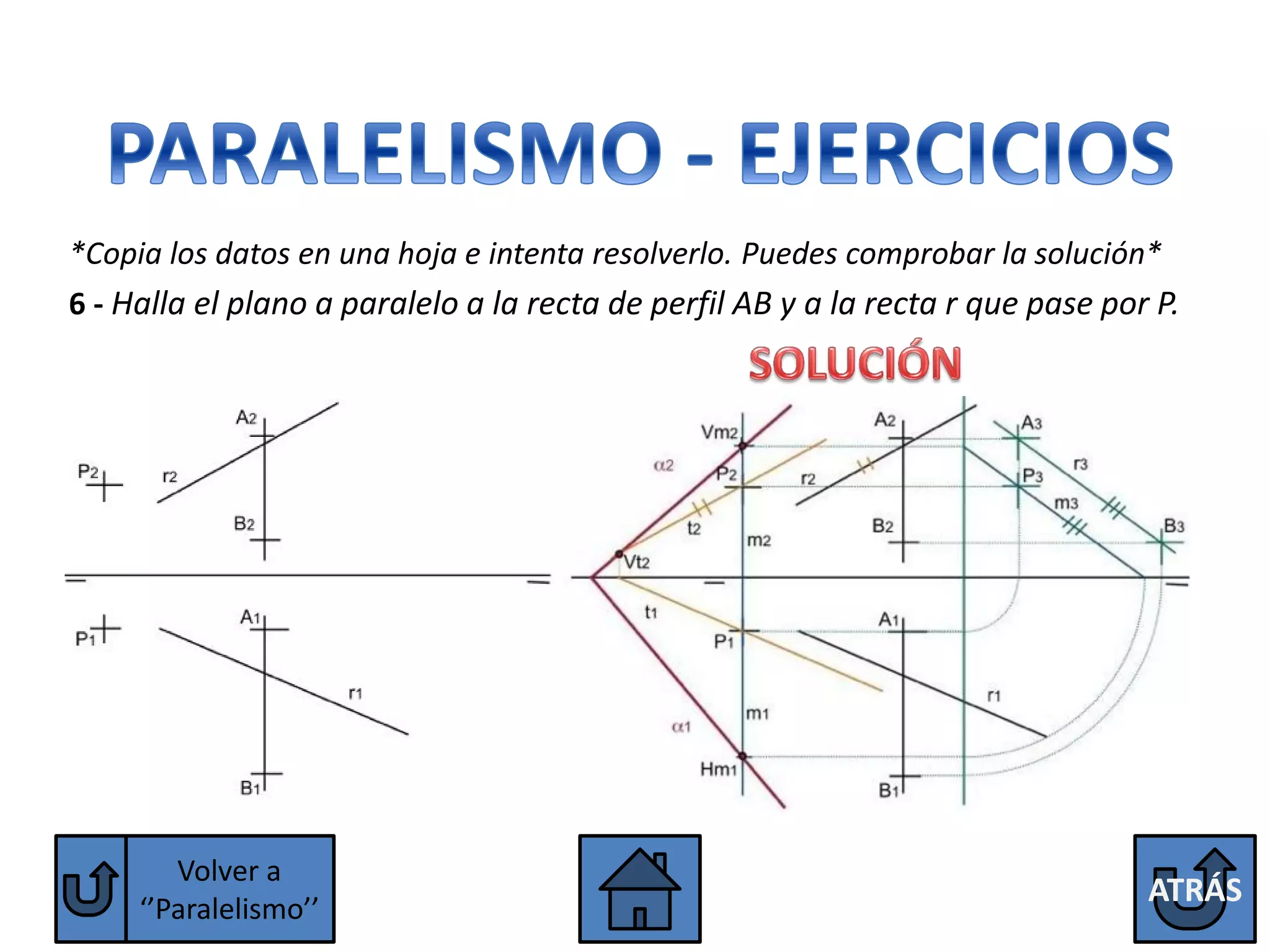
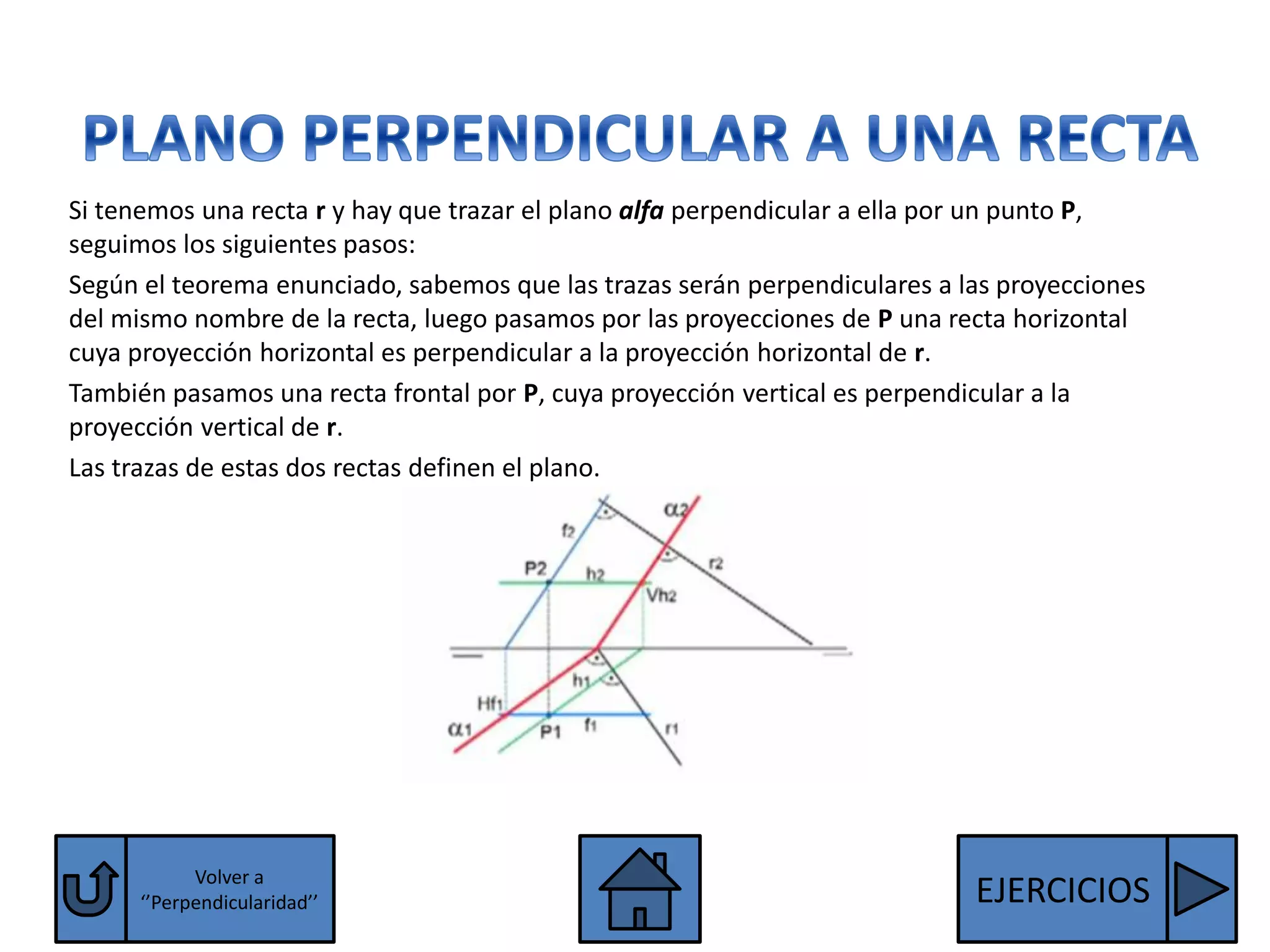
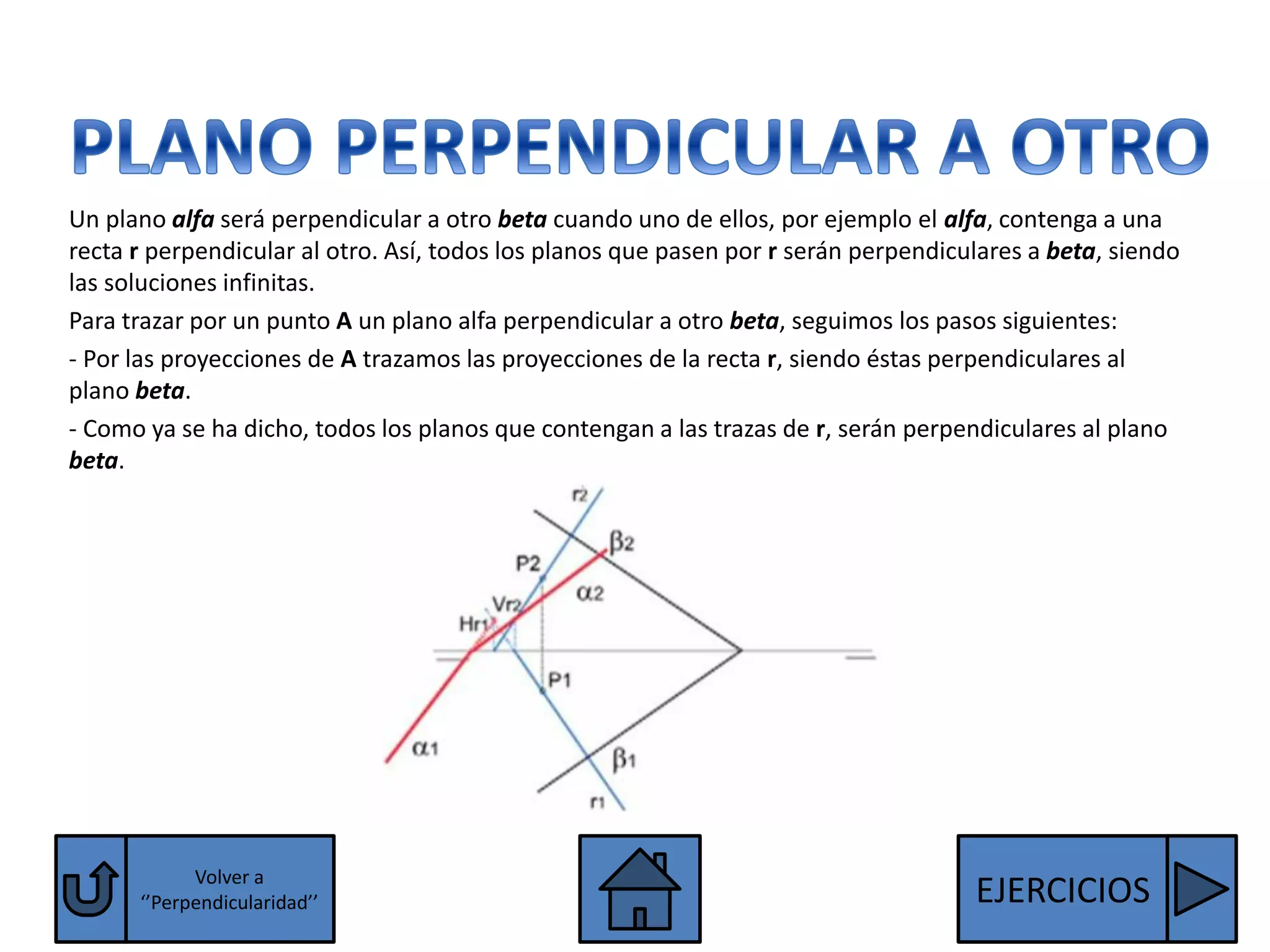
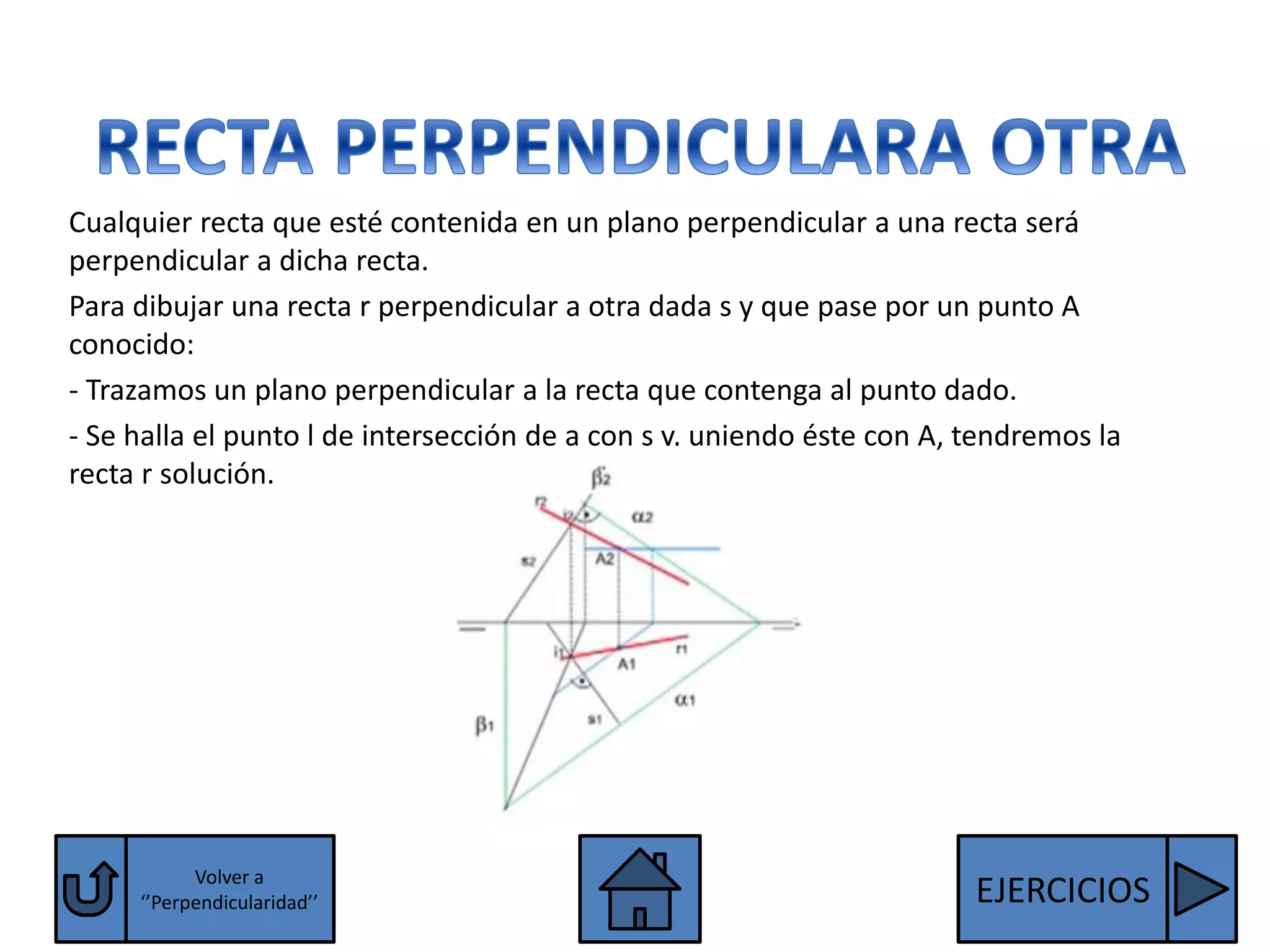
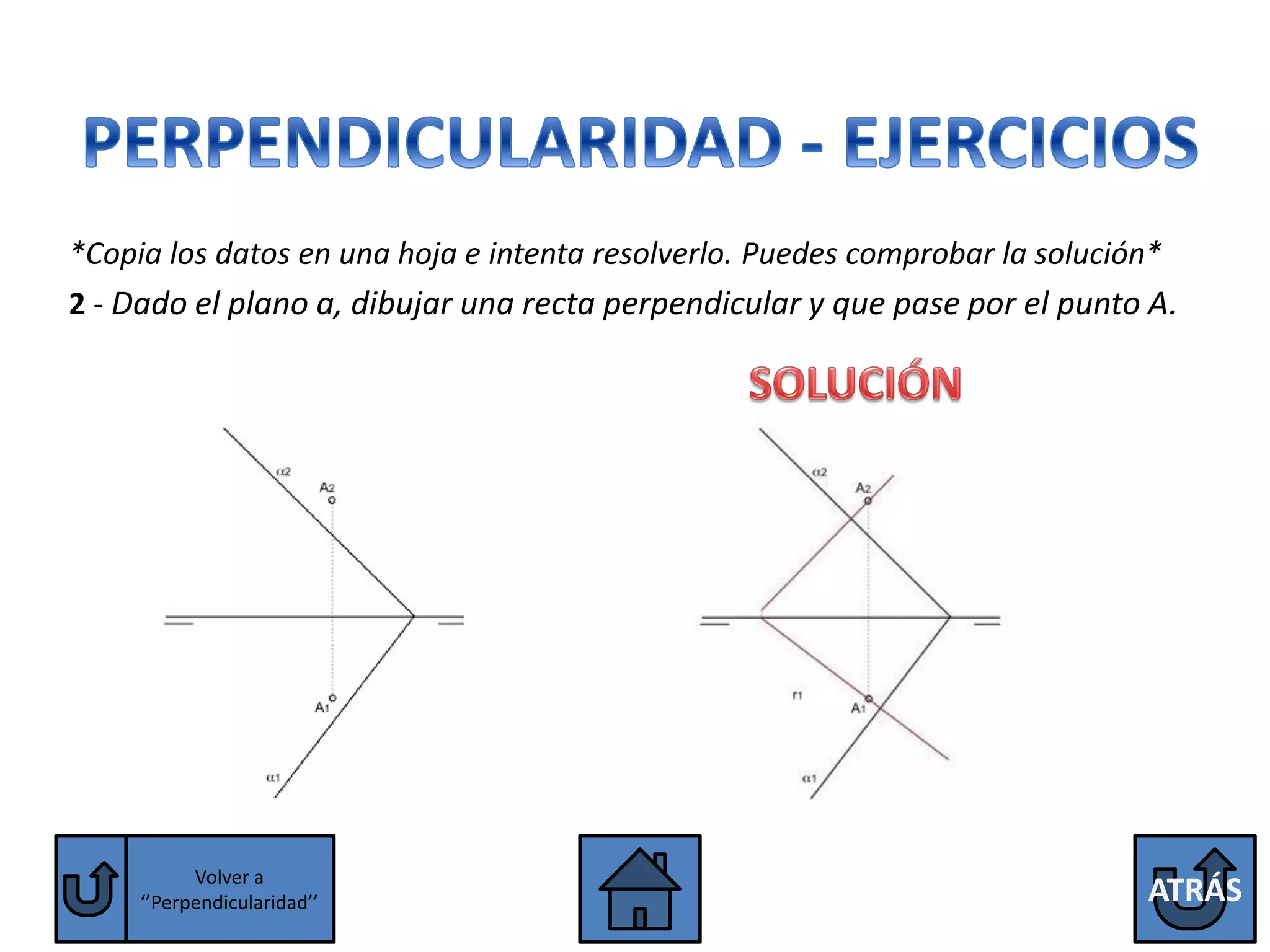
El documento explica las condiciones para que dos rectas o dos planos sean paralelos o perpendiculares. Para que dos rectas sean paralelas, sus proyecciones homónimas deben ser paralelas, excepto las rectas de perfil que también deben tener paralelas sus terceras proyecciones. Para que dos planos sean paralelos, sus trazas homónimas deben ser paralelas, excepto los planos paralelos a la línea de tierra que deben tener paralelas sus terceras trazas. Se explican también