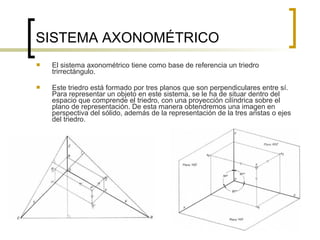
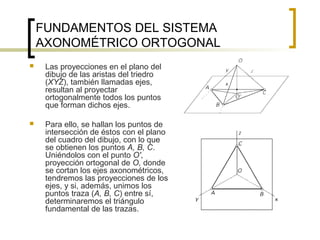
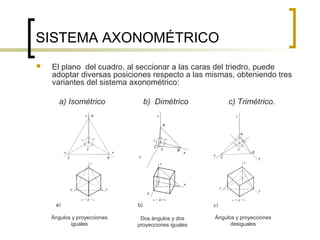
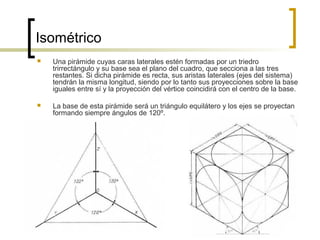
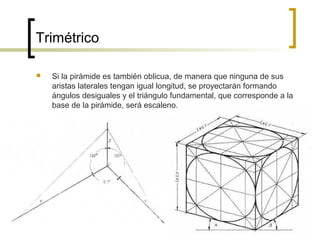
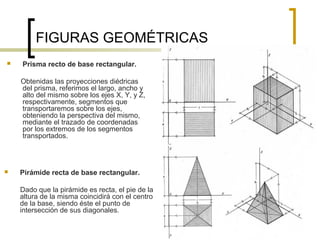
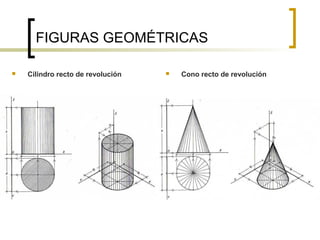
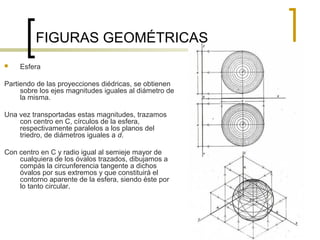
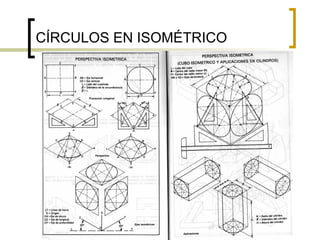
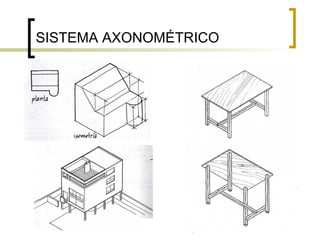
Este documento describe los sistemas de perspectiva axonométrica. Explica que la axonométrica conserva el paralelismo entre rectas y proyecta figuras tridimensionales de forma más realista. Describe los tres sistemas axonométricos (isométrico, dimétrico y trimétrico) y cómo se proyectan ángulos y ejes en cada uno. También explica cómo proyectar figuras geométricas comunes como prismas, pirámides, cilindros y esferas en los sistemas axonométricos

1. GEOMETRIA DESCRIPTIVA II
PERSPECTIVA AXONOMÉTRICA
Gabriela M. Gay Hernández

2. DEFINICION DE AXONOMETRIA
 Es la parte de la geometría descriptiva que estudia
el sistema de representación de figuras espaciales
en un plano por medio de proyecciones obtenidas
según tres ejes.
 Su característica principal es la de conservar el
paralelismo entre rectas.

3. SISTEMA AXONOMÉTRICO
 En la perspectiva axonométrica los dibujos se
ilustran en tres dimensiones, con lo cual se logra
exponer las relaciones formales de una manera
más realista.
 El sistema axonométrico permite la proyección de
los cuerpos, de forma tridimensional, siendo por lo
tanto más fácil y directa la interpretación del objeto
representado.
 El sistema es también un sistema de proyecciones
cilíndricas ortogonales.

4. SISTEMA AXONOMÉTRICO
 El sistema axonométrico tiene como base de referencia un triedro
trirrectángulo.
 Este triedro está formado por tres planos que son perpendiculares entre sí.
Para representar un objeto en este sistema, se le ha de situar dentro del
espacio que comprende el triedro, con una proyección cilíndrica sobre el
plano de representación. De esta manera obtendremos una imagen en
perspectiva del sólido, además de la representación de la tres aristas o ejes
del triedro.

5. FUNDAMENTOS DEL SISTEMA
AXONOMÉTRICO ORTOGONAL
 Las proyecciones en el plano del
dibujo de las aristas del triedro
(XYZ), también llamadas ejes,
resultan al proyectar
ortogonalmente todos los puntos
que forman dichos ejes.
 Para ello, se hallan los puntos de
intersección de éstos con el plano
del cuadro del dibujo, con lo que
se obtienen los puntos A, B, C.
Uniéndolos con el punto O',
proyección ortogonal de O, donde
se cortan los ejes axonométricos,
tendremos las proyecciones de los
ejes, y si, además, unimos los
puntos traza (A, B, C) entre sí,
determinaremos el triángulo
fundamental de las trazas.

6.  El plano del cuadro, al seccionar a las caras del triedro, puede
adoptar diversas posiciones respecto a las mismas, obteniendo tres
variantes del sistema axonométrico:
a) Isométrico b) Dimétrico c) Trimétrico.
SISTEMA AXONOMÉTRICO
Ángulos y proyecciones
iguales
Dos ángulos y dos
proyecciones iguales
Ángulos y proyecciones
desiguales

7.  Una pirámide cuyas caras laterales estén formadas por un triedro
trirrectángulo y su base sea el plano del cuadro, que secciona a las tres
restantes. Si dicha pirámide es recta, sus aristas laterales (ejes del sistema)
tendrán la misma longitud, siendo por lo tanto sus proyecciones sobre la base
iguales entre sí y la proyección del vértice coincidirá con el centro de la base.
 La base de esta pirámide será un triángulo equilátero y los ejes se proyectan
formando siempre ángulos de 120º.
Isométrico

8.  Si la pirámide es oblicua, de manera que dos de sus aristas laterales
sean de igual longitud, el triángulo de la base será isósceles y las
proyecciones de las aristas laterales formarán ángulos, dos de ellos
iguales entre sí y uno desigual.
Dimétrico

9. Trimétrico
 Si la pirámide es también oblicua, de manera que ninguna de sus
aristas laterales tengan igual longitud, se proyectarán formando
ángulos desiguales y el triángulo fundamental, que corresponde a la
base de la pirámide, será escaleno.

10.  Prisma recto de base rectangular.
Obtenidas las proyecciones diédricas
del prisma, referimos el largo, ancho y
alto del mismo sobre los ejes X, Y, y Z,
respectivamente, segmentos que
transportaremos sobre los ejes,
obteniendo la perspectiva del mismo,
mediante el trazado de coordenadas
por los extremos de los segmentos
transportados.
FIGURAS GEOMÉTRICAS
 Pirámide recta de base rectangular.
Dado que la pirámide es recta, el pie de la
altura de la misma coincidirá con el centro
de la base, siendo éste el punto de
intersección de sus diagonales.

11. FIGURAS GEOMÉTRICAS
 Cilindro recto de revolución  Cono recto de revolución

12. FIGURAS GEOMÉTRICAS
 Esfera
Partiendo de las proyecciones diédricas, se obtienen
sobre los ejes magnitudes iguales al diámetro de
la misma.
Una vez transportadas estas magnitudes, trazamos
con centro en C, círculos de la esfera,
respectivamente paralelos a los planos del
triedro, de diámetros iguales a d.
Con centro en C y radio igual al semieje mayor de
cualquiera de los óvalos trazados, dibujamos a
compás la circunferencia tangente a dichos
óvalos por sus extremos y que constituirá el
contorno aparente de la esfera, siendo éste por
lo tanto circular.

13. CÍRCULOS EN ISOMÉTRICO

14. SISTEMA AXONOMÉTRICO