Este documento presenta información sobre el análisis de radiopropagación en radioenlaces de microondas. Cubre temas como desvanecimiento multitrayecto, clasificación de desvanecimientos, métodos para calcular la probabilidad de desvanecimiento profundo como la Recomendación UIT-R PN530, y métodos para determinar el factor de aparición del desvanecimiento P0 como el método de Mojoli y el método de la UIT. El objetivo es estudiar los principales aspectos que caracterizan el desvanecimiento en radioenlaces

1. Eo 0421 - RADIOCOMUNICACIONES
Conferencia 9: Análisis de
Radiopropagación
Instructor: Israel M. Zamora, MBA, MSTM
Profesor Titular, Departamento de Sistemas Digitales y
Telecomunicaciones.
Universidad Nacional de Ingeniería
I Sem 2015

2. Objetivos
Estudiar los principales aspectos que caracterizan el
desvanecimiento en los radioenlaces de microondas.
Presentar algunos métodos para el análisis del
desvanecimiento en radioenlaces de microondas.
2I. Zamora Unidad II: Análisis de Radiopropagación

3. Contenido
• Desvanecimiento multitrayecto en radioenlaces
• Clasificación
• Desvanecimiento profundo
• Rec UIT-R PN530
• Método de Mojoli para P0
• Método de UIT para P0
• Desvanecimiento Selectivo
• Modelo de rayos
• Modelo de signatura
• Probabilidad de indisponibilidad total
• Desvanecimiento plano
• Desvanecimiento selectivo
3I. Zamora Unidad II: Análisis de Radiopropagación

4. 4I. Zamora Unidad III: Radioenlaces terrenales del servicio fijo
Reflexión y Multitrayectoria
Dispersión troposférica
(factor k)
Desvanecimiento multitrayecto en radioenlaces
Lluvia
Resulta en desvanecimiento (Fading)

5. Desvanecimiento multitrayecto en radioenlaces
Desvanecimiento:
Variación en el tiempo de la magnitud o de la fase (o de ambas) en alguna de las
componentes en frecuencias de la señal recibida, debido a cambios en las
condiciones de propagación.
5I. Zamora Unidad II: Análisis de Radiopropagación

6. • Potencia recibida nominal Po: valor mediano de la potencia recibida.
• Desvanecimiento: toda disminución de la potencia recibida de señal con relación a su
valor nominal.
• Profundidad de desvanecimiento (dB): la diferencia entre ambos valores.
• Expresada como diferencia de potencias F1=Po-P1=20log10 (ro/r1),o a partir de las tensiones
(voltajes) de envolvente r0 y r1.
Desvanecimientos:
Duración del desvanecimiento F1
Depresión de Pearson:
mttPPF
ttPPF


,
,
202
1101
121 tt 
fPP  0
Desvanecimiento multitrayecto en radioenlaces
6I. Zamora Unidad II: Análisis de Radiopropagación

7.  Multitrayecto: atmosféricos y suelo (u otros).
 Suele ser muy profundo y selectivo en frecuencia (afectan solo una parte de la banda
de frecuencia)
 Forman ISI.
 Se modela como Rayleigh o Rice
 Centelleo
 Irregularidades en la troposfera
 De pequeña intensidad
 Factor k
 Desvanecimiento lento de duración larga, con hasta 6 dB de profundidad
 El radio de Fresnel depende de la frecuencia, aún así la variación no es significativa
dentro del canal. Por ello se consideran planos (afectan a toda la banda de
frecuencia).
 También pueden ocurrir desvanecimientos por
mecanismos de superrefracción y formación de
conductos que desenfocan el haz radioeléctrico.
 Este grupo se modela como una gaussiana o
expresiones empíricas.
 Los desvanecimientos de factor k pueden evitarse
mediante alturas de antenas adecuadas.
7I. Zamora Unidad II: Análisis de Radiopropagación
Desvanecimiento multitrayecto en radioenlaces

8. Desvanecimiento multitrayecto en radioenlaces
Clasificación de los desvanecimientos:
8I. Zamora Unidad II: Análisis de Radiopropagación

9. : factor de actividad multitrayecto (%)
1-: propagación en condiciones normales
Multitrayectos atmosféricos:
 “Mes más desfavorable” para estadísticas de:
 Climas templados: η “para el año medio” se corresponde con los 3 meses del verano:
 Desvanecimiento por multitrayectoria, es el
factor dominante para frecuencias por debajo
de10GHz.
 Por encima de 10GHz, las precipitaciones
determinan la longitud aceptable del trayecto.
.desfmes
.. 4/112/3 desfmesdesfmes   
 Obviamos el suelo y estudiamos:
 dependencia con distancia, gradiente N, espesor, altura y grado de estratificación
atmósfera.
 Si existe componente dominante ⇒ Distribución Rice.
 Ej: radioenlaces
 Si no existe componente dominante ⇒ Distribución Rayleigh
 Ej: com. Móviles (reflexiones en edificios,dispersión, difracción)
9I. Zamora Unidad II: Análisis de Radiopropagación

10. •Objetivo: Rec UIT-R PN530
 Evaluar la probabilidad de que se rebase una determinada profundidad de desvanecimiento
F1(dB) ⇒ p(F>F1).
 Se predice la duración media de los desvanecimientos
 Se predice la frecuencia de los desvanecimiento: número de desvanecimientos de
profundidad superior a F por unidad de tiempo.
1. Si F es pequeña, usualmente centelleo F ≈ 2-5 dB se aplica una gaussiana. La
probabilidad de rebasar F1 se expresa mediante:
2. Si F es grande, F > 15 dB, se aplican estadísticas derivadas de la función Rayleigh.







G
G
F
erfFFp

1
1
2
1
)(
10I. Zamora Unidad II: Análisis de Radiopropagación
 Sea r la tensión o voltaje de la envolvente de la señal recibida.
 La pdf de r en el modelo de desvanecimiento Rayleigh: 2
2
1)( r
x
R exrp 


⇒
Desvanecimientos Profundos
  10
22
10/
11
11
10
110
exp1
F
rr
F
RR rrpR)FF(p











11. Desvanecimientos Profundos
11I. Zamora Unidad II: Análisis de Radiopropagación
 La probabilidad absoluta de que el desvanecimiento sea superior a F1 (dB) incluye la
probabilidad de que se ocurra este tipo de desvanecimiento p(R)=η,
 RFFp)Fp(F R 11  
    )(111 FpRFFp)Fp(F GR  
 La ITU-R proporciona la siguiente relación empírica entre η y P0:
 Donde: 20
r
P


 Factor de aparición del desvanecimiento.
 Por tanto podemos escribir: 10
01
1
10
F
P)p(F


Po depende de :
• Longitud
• Frecuencia
• Terreno
• Clima
 75.0
02.0exp1 P
Para el caso de desvanecimiento profundo F > 15 dB pG(F)  0, por lo cual la ecuación se reduce a:
10
0
10
21
11
1010
FF
r
P)Fp(F




NOTA: Esta expresión la vamos a utilizar para determinar la probabilidad de indisponibilidad
debido al desvanecimiento plano, pTP
10
0
1
10
F
TP Pp



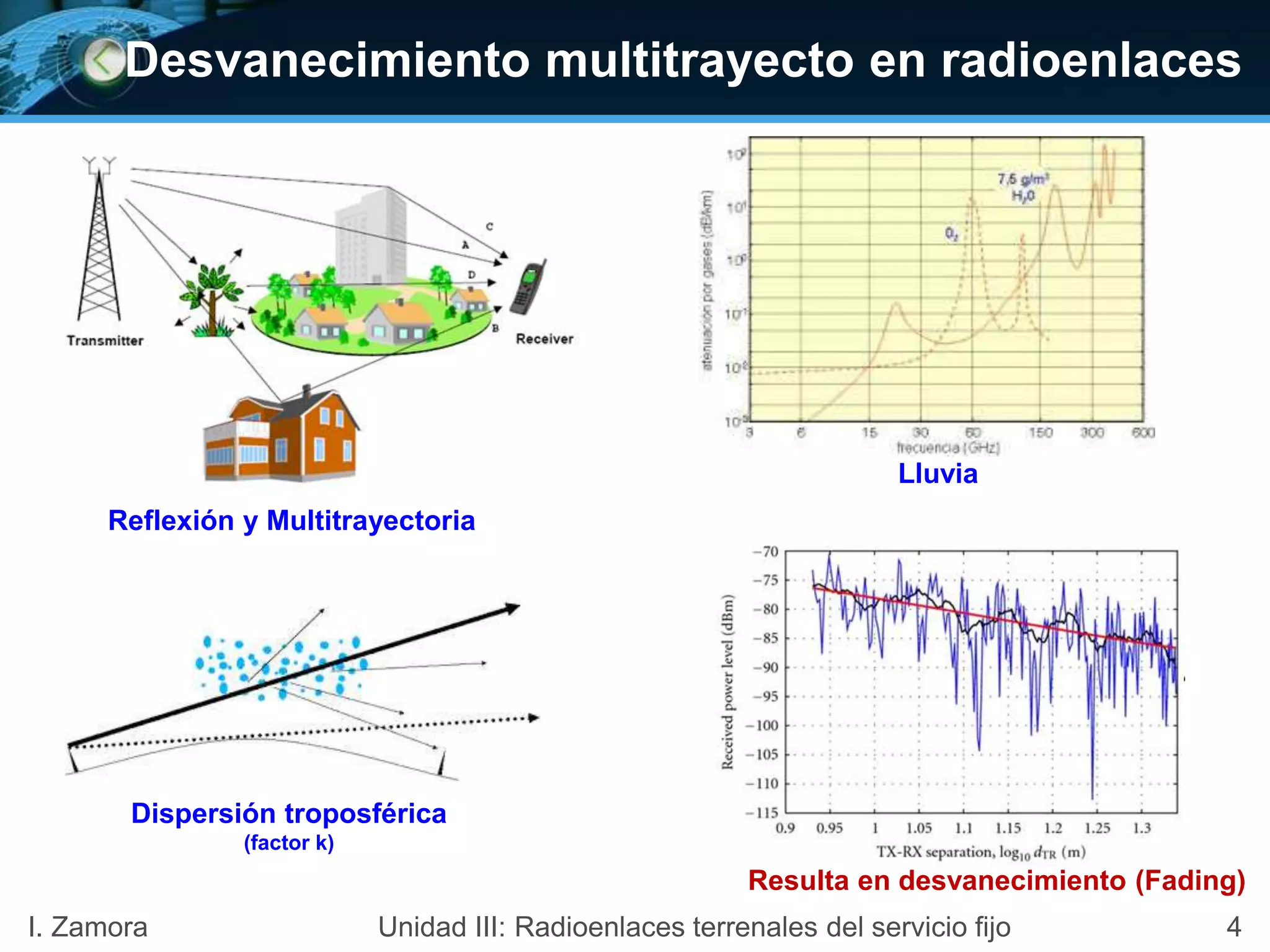
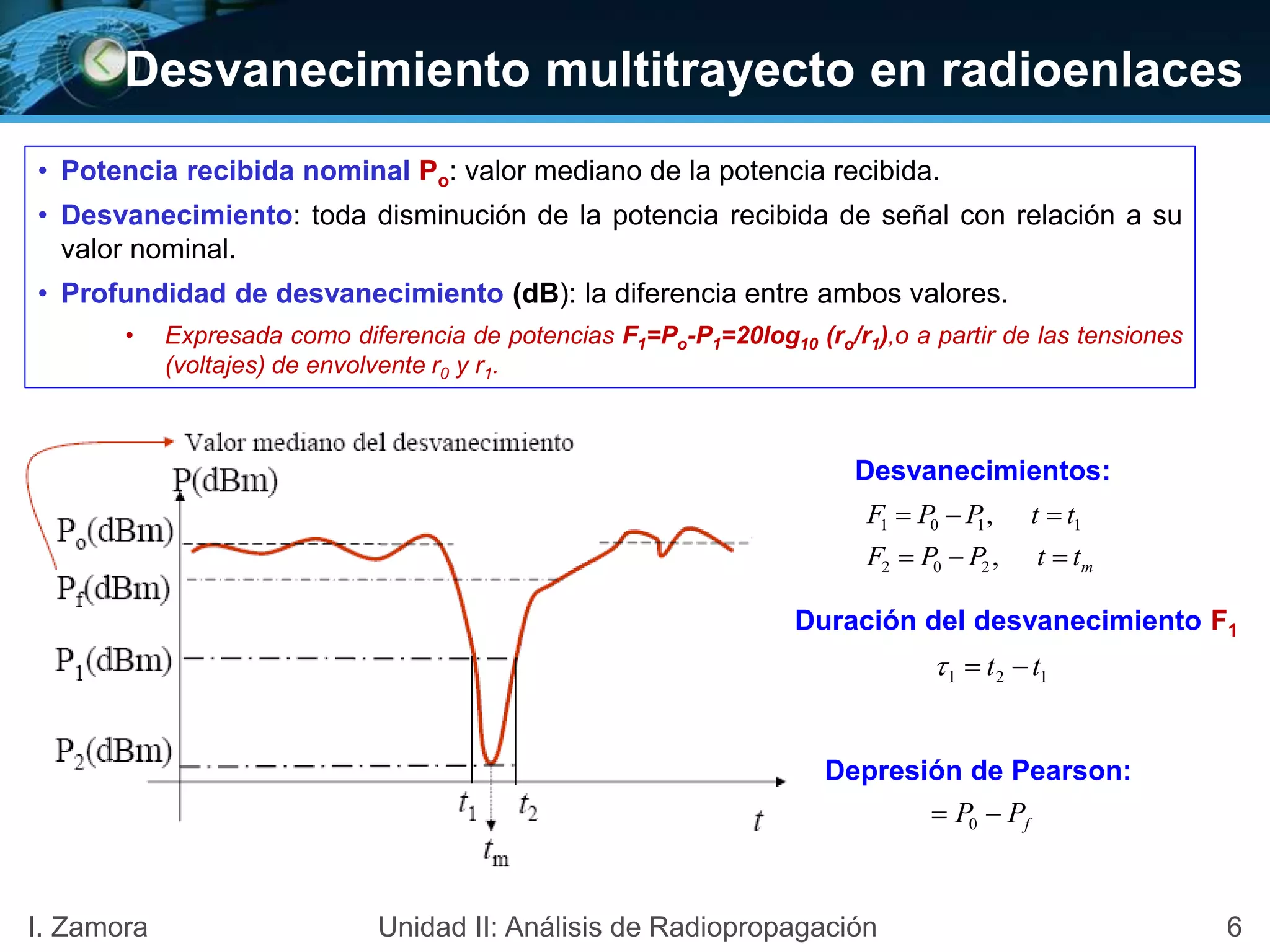
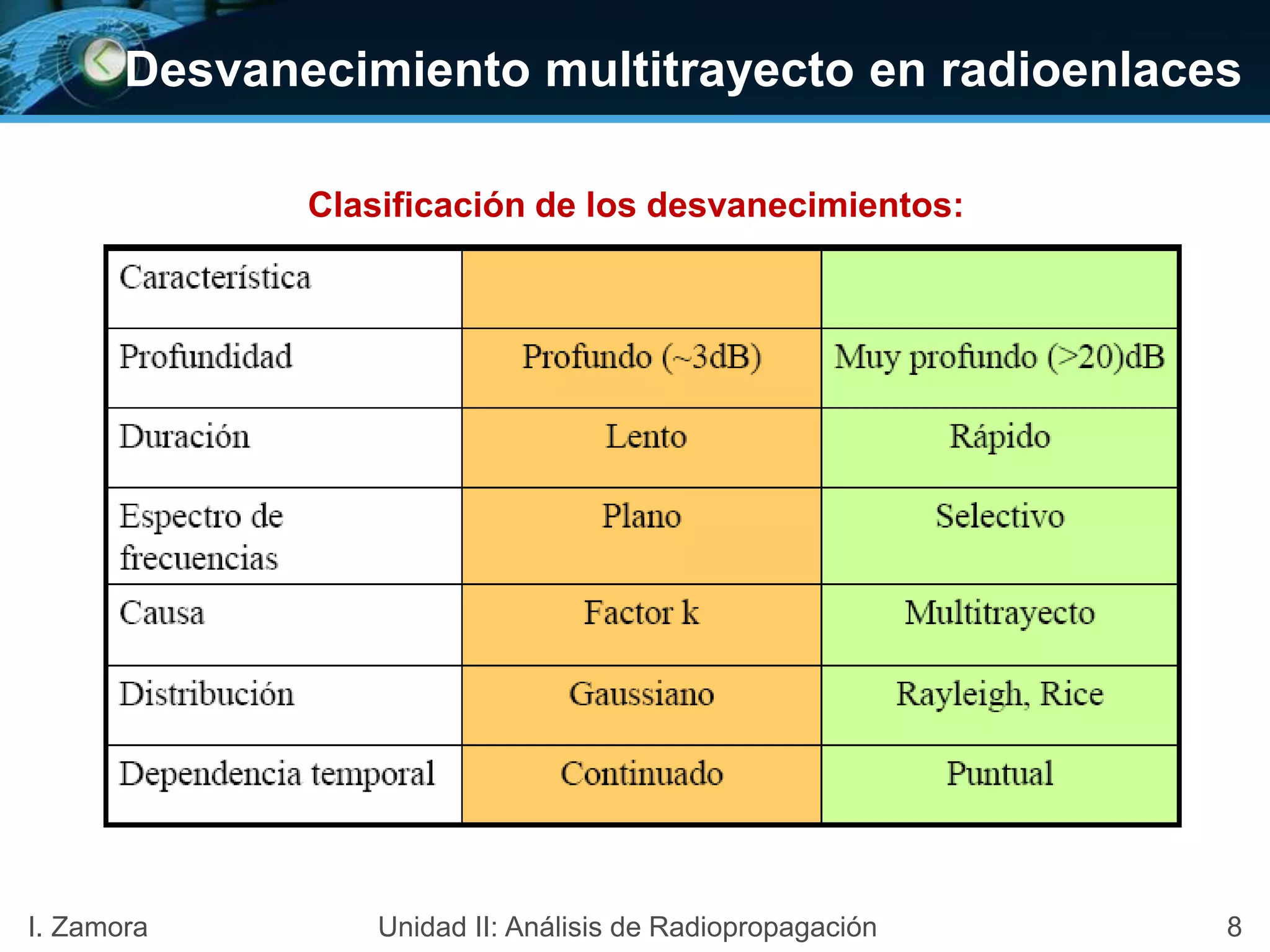
12. Desvanecimiento: Método de Mojoli para P0
12I. Zamora Unidad II: Análisis de Radiopropagación
 El valor del factor de aparición del desvanecimiento, P0, para el mes más desfavorable se
calcula como sigue,
 Donde:
 f es frecuencia en GHz
 d es la longitud del enlace en Km
 a es un parámetro descriptivo del clima. a  [.25,4].
 Climas templados a=1,
 Climas secos y montañosos, a=0.25,
 Climas húmedos o que presentan variaciones térmicas intensas (ej: desiertos), a=4.
 b parámetro que incluye la influencia del terreno. Se calcula como:
 s es la desviación típica terreno sin tener en cuenta el primer y
último km
3
0
34
3.0 












df
baP
 Para terrenos medianamente ondulados con una ondulación s: comprendida entre 5 y 100 m.
 Terrenos muy accidentados toman valores mayores.
3.1
15








s
b
Objetivo: predicción de la probabilidad de desvanecimiento, para el peor mes
del año en cualquier parte del mundo

13. Desvanecimiento: Método de Mojoli para P0
13I. Zamora Unidad II: Análisis de Radiopropagación
    27.0
3
15
4
4.2
048.025.03.0
3
0 











P048.0
15
155
3.1








b
Ejemplo 1: Determine el factor de actividad de multitrayecto y la probabilidad de
indisponibilidad (interrupción) por desvanecimiento plano, de radioenlace que cubre una
distancia de 15Km, operando a la frecuencia de 2.4Ghz, y margen bruto de desvanecimiento
del orden de los 41dB. Considere todos los otros factores que inciden cuando el radioenlace ha
sido implementado en la región del pacífico del país. La base del terreno muy irregular, siendo
la ondulación promedio de 155m.
  %)21.7(0721.0)27.0(2.0exp1 75.0

  %)0021.0(000021.01027.0 10
41


TPp
Solución: En este caso se requiere encontrar  (factor de actividad del multitrayecto) y pTP
(probabilidad de indisponibilidad por desvanecimiento plano). Para ello, primero hay que encontrar
P0 (factor de aparición del desvanecimiento), considerando que para el escenario del enlace a=0.25
(clima seco), mientras encontramos b, para un valor medio de ondulación (s=100m), como sigue:
Ahora hallamos:
Entonces,  (factor de actividad del multitrayecto) es:
Y pTP (probabilidad de indisponibilidad por desvanecimiento plano), se obtiene considerando que
M  F  F=M= 41dB:

14.  Cálculo de la probabilidad de desvanecimiento:
Métodos 1 y 2 propuesto en Rec 530 ITU-R
Objetivo: predicción de la probabilidad de desvanecimiento, para el peor mes
del año en cualquier parte del mundo
Dos métodos
 Método 1:
Para pequeños porcentajes de tiempo
Para grandes profundidades de desvanecimiento
No se utiliza el perfil del trayecto
Útil para la planificación inicial o solicitud de licencia de un radioenlace
 Método 2
Para cualquier profundidad de desvanecimiento, mezcla de:
Método para desvanecimientos profundos
Interpolación para desvanecimientos poco intensos
14I. Zamora Unidad II: Análisis de Radiopropagación
Se desarrollará el método 1.
Desvanecimiento: Método de UIT para P0

15. 15I. Zamora Unidad II: Análisis de Radiopropagación
 Método 1 de la Rec. 530 ITU-R.
 Validez: desde fmin=15/d(GHz) hasta 45 GHz
 Error: 5.2dB a 7.3 dB
 Se siguen los siguientes pasos:
1) Cálculo del valor geoclimático del trayecto, K, en el mes más desfavorable
 A partir de datos de desvanecimientos en la zona
 O estimándolo con:
Donde:
dN1: valor del gradiente para los 65 m inferiores de la atmósfera, no superado durante el 1% del tiempo
sa: rugosidad del suelo.
42.0003.09.3 1
10 
 a
dN
sK
Para una estimación rápida se puede utilizar: 1029.02.4
10 dN
K 

2) Se calcula el ángulo de inclinación del trayecto |εp| (mrad) y la altura
mínima hL mediante:
dhhp /21   21,min hhhL 
donde h1y h2 son las alturas de las antenas en m sobre el nivel del mar y des la longitud del
trayecto en km.
Desvanecimiento: Método de UIT para P0

16. 16I. Zamora Unidad II: Análisis de Radiopropagación
donde f está en GHz y d en km.
Para una estimación rápida se puede utilizar
usando el valor aproximado de K
3) El valor de la probabilidad p(F), en %, es
   
(%)101)( 10/00085.0032.097.02.3 Fhf
p
L
dKFp 
 
   
(%)101)( 10/001.0033.02.13 Fhf
p
L
dKFp 
 
Desvanecimiento: Método de UIT para P0
10
0
1
10)(
F
TP PpFp

Donde:
Por lo que:    
(%)101 00085.0032.097.02.3
0
Lhf
pdKP 
 

17. 17I. Zamora Unidad II: Análisis de Radiopropagación
La aparición de trayectos múltiples en sistemas de banda ancha da lugar a
la existencia de un fading selectivo en frecuencia, que provoca distorsión
en la señal (ISI).
 Existen varios modelos que caracterizan la función de transferencia del
canal:
 Modelo de rayos (2, 3, general)
 Modelos polinómicos
 Modelos paramétricos
 Para la predicción de interrupciones se han aplicado varios enfoques
en función del modelo de canal y de la caracterización de los equipos:
 Método del margen neto contra los desvanecimientos
 Métodos de las curvas de signaturas
 Métodos que utilizan la distorsión lineal de amplitud.
Desvanecimiento Selectivo

18. 18I. Zamora Unidad II: Análisis de Radiopropagación
 Modelos de Rayos
 El modelo general de rayos ofrece una función de transferencia:
 



N
i
j
i
ii
eaH
0
)( 
  ai es la amplitud
  es el retardo
 i es la fase del rayo i-ésimo.
 El modelo mas sencillo es el de tres rayos simplificado:
 
)(1)( 1221
3
0
21
 
 


 jj
i
j
i eaeaeaH ii
 
  2/2/2/1)( BBebaH j
 
 
,0
notch
Un rayo directo de amplitud 1, un rayo de
amplitud b con retardo  >0, y un factor de
proporcionalidad a.
b < 1, fase mínima
b > 1, fase no mínima.
Desvanecimiento Selectivo: modelo de rayos

19. 19I. Zamora Unidad II: Análisis de Radiopropagación
o Se tiene así para : 0,
1
)( 



 


m
ep
m
o Suponiendo que b y  son estadísticamente independientes, la fdp de b y  son
de tipo exponencial.
o Para m se ha propuesto el valor :
)(),(
50
7.0
3.1
Kmdns
d
m 






o Para b, la función de densidad es:
 depende de d, f, tipo terreno y clima.
10,
1
)( 

 
b
e
bpb 

Desvanecimiento Selectivo

20. 20I. Zamora Unidad II: Análisis de Radiopropagación
Desvanecimiento Selectivo: modelo de signatura
 Modelos de Signatura o Firma
 La signatura o firma de un receptor en un radioenlace digital es una
caracterización de los equipos, para un modelo de canal determinado.
 Para el modelo de rayos, la signatura es la curva del valor máximo de
desvanecimiento en función de f0 a partir del cual se sobrepasa una
proporción de errores determinada.
• La signatura de un Rx, para el par (BERo,) → B(fo )
• La resistencia al desvanecimiento selectivo será mayor cuanto mas estrecha y baja sea
la curva de signatura.
• La zona interior a la curva supone una BER mayor que para la que se ha obtenido la
curva. La zona exterior, es para una BER menor.

21. 21I. Zamora Unidad II: Análisis de Radiopropagación
Comentarios acerca de la signatura
 Interesa signatura estrecha y baja
 La altura depende de la modulación,
si existe o no igualación, y de .
 La anchura no depende de  y sí de la
modulación y ecualización.
 Generalmente se muestra para  =
6.3nsg
 La signatura de equipos modernos es
casi cuadrada
Probabilidad de indisponibilidad debido al desvanecimiento selectivo
  oppTS

 , es la probabilidad de desvanecimiento multitrayecto (ya
visto antes)
 p(o/), es la probabilidad de desvanecimiento selectivo,
condicionada a desvanecimiento multitrayecto
Desvanecimiento Selectivo: modelo de signatura

22. 22I. Zamora Unidad II: Análisis de Radiopropagación
 La probabilidad p(o| η) se puede calcular a través de la signatura, como:
 C: Factor Constante
 pb(1): Valor de la pb de b para b=1. Se toma de una tabla (ver abajo).
 k: Signatura normalizada, constante que depende de la signatura.
 Existen valores típicos para distintos Rx, con y sin ecualización, según el esquema
de modulación
 O se calcula a partir de la curva de signatura del receptor
 < τ 2>: varianza del retardo del eco.
 Ts, periodo de símbolo
 El proceso queda:
1) Factor de actividad multitrayecto:
2) Se elige el valor de pb(1):
  22
/)1( sb TkpCop  
 75.0
02.0exp1 P
Desvanecimiento Selectivo: modelo de signatura

23. 23I. Zamora Unidad II: Análisis de Radiopropagación
3) a. Se toma valor típico de la
signatura normalizada, k, de:
3) b. O se calcula a partir del ancho W(MHz) y alto BC(dB) de la signatura, con:
4) Si se supone el retardo distribuido exponencialmente,
m es el valor medio del retardo, con:
5) Finalmente, se calcula:
)(),(
50
7.0
3.1
Kmdns
d
m 






  20/
10 CBs
BsA
T
KTMHzWK 


y Ts y  en seg
22
2 m 






 2
2
2)1(
s
m
bTS
T
kpCp


Desvanecimiento Selectivo: modelo de signatura
Una aproximación práctica
propuesta por Mojoro considera
C=1 y C·pb(1) ·2 = 4.32






 2
2
32.4
s
m
TS
T
kp


BA KKk Entonces:

24. 24I. Zamora Unidad II: Análisis de Radiopropagación
Desvanecimiento total: Plano mas Selectivo
Para determinar la indisponibilidad o interrupción total por desvanecimiento, se
suman los porcentajes de indisponibilidad de cada vano
También se usa la expresión más restrictiva:
 Se distingue entre radioenlaces de Pequeña capacidad y Media/Alta.
 Pequeña capacidad (< 34Mbps) → Sólo Desvanec. Plano
o Probabilidad de que el desvanecimiento sea mayor que F=M3, donde M3 es el margen de enlace
correspondiente a una tasa de errores de bit BER=10-3.
o Para un factor de aparición de desvanecimiento Po
 Capacidad Media/Alta (> 34Mbps)
• Se consideran ambas contribuciones pTP y pTS.
TSTPTT ppp  • Desvanecimiento plano
• Desvanecimiento selectivo
  5.1
/22/2/
 

,TSTP
pppTT
10
0
3
10
M
TPTT Ppp


NOTA: En la unidad III se profundizará sobre este tema en el contexto de la
evaluación de la disponibilidad y calidad de un radioenlace.

25. 25I. Zamora Unidad II: Análisis de Radiopropagación
Ejemplo 2: Considere los datos y resultados del ejemplo 1 para este ejemplo, pero además
asuma que el radioenlace utiliza polarización vertical, para una transmisión de información de
140 Mbits/s, utilizando modulación 16 QAM, con ecualización.
Solución: Partimos que conocemos el valor de  (factor de actividad del multitrayecto) y pTP
(probabilidad de indisponibilidad por desvanecimiento plano). Resta determinar la pTS
(probabilidad por desvanecimiento selectivo) para lo cual necesitamos encontrar el valor de k
(signatura normalizada) y m (tiempo medio de retardo).
En el caso de k, dado que conocemos la modulación y disponemos de una tabla para el caso
con ecualización tomamos el valor correspondiente:
Desvanecimiento Total: Plano mas Selectivo
(ns)..
.
m 1460
50
15
70
31







3.0k
Ahora, determinamos m como:

26. 26I. Zamora Unidad II: Análisis de Radiopropagación
En vista que no tenemos mas detalles del caso de análisis, utilizaremos la expresión propuesta
por Mojoro para determinar pTS, tomando el valor de =0.0721 del ejemplo 1, y para Ts (tiempo
de duración de un pulso digital) en un esquema 16 QAM, , tenemos:
Desvanecimiento Total: Plano mas Selectivo
%)002344.0(00002344.0
00000244.0000021.0


 TSTPTT ppp
     %000244000000244.0
57.28
146.0
3.00721.032.4
2
.pTS 






ns
MbpsR
M
R
T
bs
s 57.28
140
16loglog1 22

Entonces, pTS es:
Puede verse que para la frecuencia dada (2.4GHz) pTP es mucho mayor que pTS por lo que
el resultado es básicamente el mismo que pTP. No obstante, se obtenemos el valor exacto
tenemos:

27. • Lectura Obligatoria
• Transmisión por Radio
• Capítulo 3
Sección 3.18
• Capítulo 5
Sección 5.9
• Lectura Recomendada
• Ninguna.
27I. Zamora Unidad II: Análisis de Radiopropagación