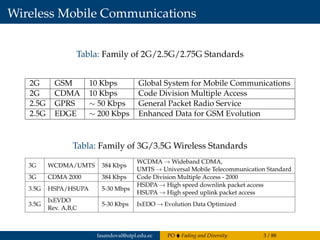
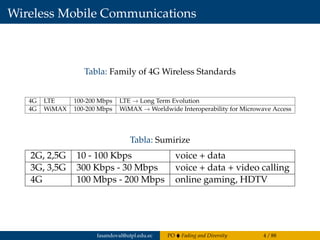
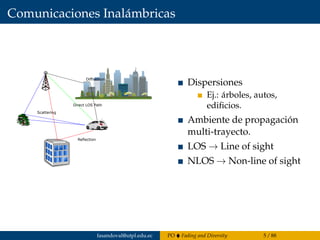
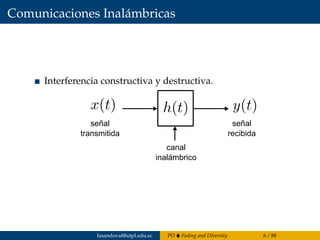
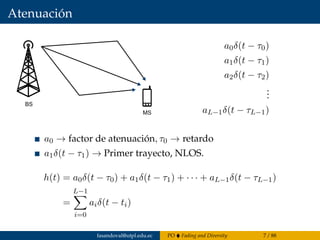
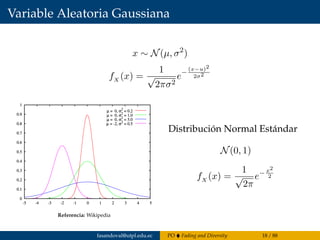
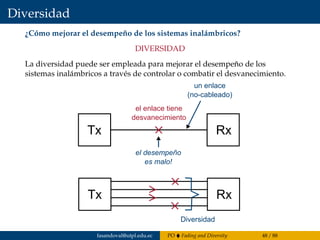
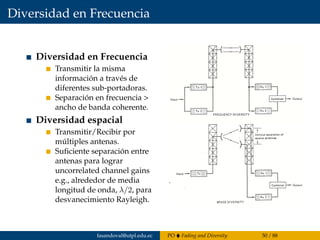
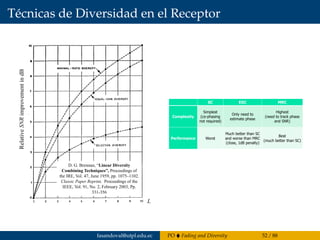
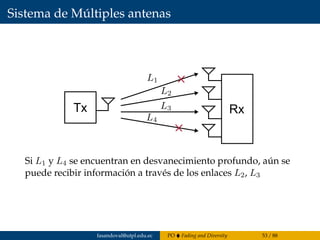
El capítulo 4 del documento de Francisco Sandoval se centra en la propagación de ondas, abordando el fading y la diversidad en sistemas de comunicación inalámbricos y cableados. Se discuten diferentes tipos de desvanecimiento, el impacto del canal con desvanecimiento Rayleigh y la importancia de la diversidad para mejorar el rendimiento del sistema. Además, se presentan estándares de tecnologías móviles 2G a 4G y conceptos estadísticos relacionados con el coeficiente de desvanecimiento.












![Teorema del Límite Central
Enunciado Formal
Sea X1, X2, · · · , Xn un conjunto de variables aleatorias,
independientes e idénticamente distribuidas de una
distribución con media µ y varianza σ2 = 0. Entonces, si n es
suficientemente grande, la variable aleatoria
¯x =
1
n
n
i=1
xi
tiene aproximadamente una distribución normal con µ¯x = µ y
σ¯x2 = σ2
n [Wikipedia, 2016b].
“El TLC indica que, en condiciones muy generales, si Sn es la suma
de n v.a’s independientes y de varianza no nula pero infinita, entonces
la función de distribución de Sn «se aproxima bien» a una
distribución normal o Gaussiana.” [Wikipedia, 2016b]
fasandoval@utpl.edu.ec PO Fading and Diversity 19 / 88](https://image.slidesharecdn.com/dfadinganddiversity-190219172211/85/Tema-4-Fading-and-diversity-21-320.jpg)





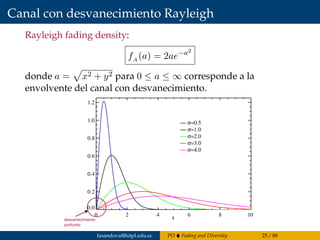
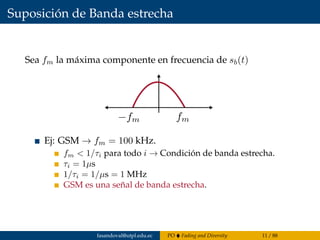
![Canal con desvanecimiento Rayleigh
fΦ (φ) =
∞
0
a
π
e−a2
da
=
∞
0
1
2π
(2aea2
)da
=
1
2π
−e−a2 ∞
0
fΦ (φ)=
1
2π
.
Que corresponde a una distribución uniforme entre [−π, π].
fA,Φ (a, φ) =
a
π
e−a2
=
1
2π
2ae−a2
= fΦ (φ) · fA (a),
dado que A y φ son variables aleatorias independientes.
fasandoval@utpl.edu.ec PO Fading and Diversity 26 / 88](https://image.slidesharecdn.com/dfadinganddiversity-190219172211/85/Tema-4-Fading-and-diversity-28-320.jpg)


![Ejemplo: Canal con desvanecimiento Rayleigh
¿Cuál es la probabilidad de que la fase φ ∈ [−π/3, π/3]?
fasandoval@utpl.edu.ec PO Fading and Diversity 28 / 88](https://image.slidesharecdn.com/dfadinganddiversity-190219172211/85/Tema-4-Fading-and-diversity-31-320.jpg)
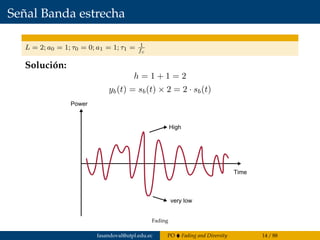
![Ejemplo: Canal con desvanecimiento Rayleigh
¿Cuál es la probabilidad de que la fase φ ∈ [−π/3, π/3]?
Solución:
P(−π/3 ≤ φ ≤ π/3) =
π/3
−π/3
1
2π
dφ
=
1
2π
π
3
− −
π
3
=
1
2π
·
2π
3
=
1
3
fasandoval@utpl.edu.ec PO Fading and Diversity 28 / 88](https://image.slidesharecdn.com/dfadinganddiversity-190219172211/85/Tema-4-Fading-and-diversity-32-320.jpg)




















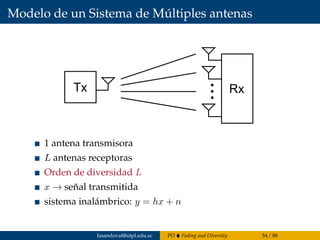
![Diversidad en Tiempo
Dispersión de las señales de información a través de múltiples
intervalos de tiempo.
Repetition coding: Transmitir la misma señal repetidas veces a través de
múltiples tiempos coherentes (separación en tiempo > tiempo
coherente) → ancho de banda ineficiente!!!
Error Control Coding: Esquema mucho más sofisticado.
Coding and interleaving
Tse and Viswanath: Fundamentals of Wireless Communications 73
00
00
00
00
00
11
11
11
11
11
00
00
00
00
00
11
11
11
11
11
000000
111111
000000
111111 00
00
00
00
00
11
11
11
11
11
000000
111111
000000
111111 00
00
00
00
00
11
11
11
11
11
00
00
00
00
00
11
11
11
11
11
00
00
00
00
00
11
11
11
11
11
000000
111111
000000
111111
000000
111111
00
00
00
00
00
11
11
11
11
11
00
00
00
00
00
11
11
11
11
11
000000
111111
000000
0000
111111
1111
000000
0000
111111
1111
000000
111111
000000
111111
000000
111111
000000
111111000000
0000
111111
1111
000000
0000
111111
1111
000000
0000
111111
1111
000000
0000
111111
1111
000000
0000
111111
1111
000000
0000
111111
1111
0000
00
1111
11
0000
00
1111
11
0000
00
1111
11
0000
00
1111
11
Interleaving
x2
Codeword
x3
Codeword
x0
Codeword
x1
Codeword
|hl|
L = 4
l
No Interleaving
Figure 3.5: The codewords are transmitted over consecutive symbols (top) and inter-
Referencia: [Tse and Viswanath, 2005]
fasandoval@utpl.edu.ec PO Fading and Diversity 49 / 88](https://image.slidesharecdn.com/dfadinganddiversity-190219172211/85/Tema-4-Fading-and-diversity-57-320.jpg)
![Técnicas de Diversidad en el Receptor
Transmitter sends same signal over L independent fading paths
obtained by diversity in time, space, frequency (repetition codin
LinearCombiner
Most combiners are linear (weigh
sum of branches)
y = hx + n
y = [y1, · · · , yL]T
h = [h1, · · · , hL]T
= [r1ejθ1,··· ,rLejθL
]T
n = [n1, · · · , nL]T
∼ CN(0, N0IL)
Most combiners are linear
(weighted sum of
branches)
yΣ = (wT
h) · x + (wT
n)
w = [w1, · · · , wL]T
fasandoval@utpl.edu.ec PO Fading and Diversity 51 / 88](https://image.slidesharecdn.com/dfadinganddiversity-190219172211/85/Tema-4-Fading-and-diversity-59-320.jpg)



![Detección de la señal
Potencia de ruido:
Potencia de ruido = E (wH
n)(wH
n)∗
= E wH
nnH
w
= wH
E nnH
w
Sea n = [n1, n2, · · · , nL]T
, entonces
nnH
= [n1, n2, · · · , nL]T
[n1, n2, · · · , nL]
=
|n1|2
n1n∗
2 · · · · · ·
n2n∗
1 |n2|2
· · · · · ·
...
...
...
...
· · · · · · · · · |nL|2
y por tanto,
E[nn]H
=
σ2
n 0 0 0
0 σ2
n 0 0
...
...
...
...
· · · · · · · · · σ2
n
= σ2
nI
fasandoval@utpl.edu.ec PO Fading and Diversity 58 / 88](https://image.slidesharecdn.com/dfadinganddiversity-190219172211/85/Tema-4-Fading-and-diversity-66-320.jpg)



![Detección de la señal
Por tanto, el vector óptimo beamformer w que maximiza el
SNR recibido es [maximal ratio combining (MRC)]
wopt =
h
h
Por tanto:
SNR = wH
h
2 P
σ2
n
=
hH
h
h
2
P
σ2
n
= h 2 P
σ2
n
fasandoval@utpl.edu.ec PO Fading and Diversity 62 / 88](https://image.slidesharecdn.com/dfadinganddiversity-190219172211/85/Tema-4-Fading-and-diversity-70-320.jpg)
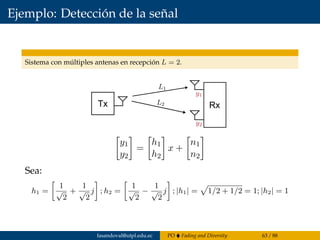



![Chi-Squared
Chi-Squared - Definición
“La distribución de Pearson,
llamada también ji cuadrada(o)
o chi cuadrado(a) (X2), es una
distribución de probabilidad
continua con un parámetro k
que representa los grados de
libertad de la variable aleatoria
X = Z2
1 + · · · + Z2
k
Donde Zi son variables
aleatorias normales
independientes de media cero
y varianza uno
[Wikipedia, 2016a]”.
Función distribución de probabilidad
Referencia: [Wikipedia, 2016a]
fasandoval@utpl.edu.ec PO Fading and Diversity 67 / 88](https://image.slidesharecdn.com/dfadinganddiversity-190219172211/85/Tema-4-Fading-and-diversity-75-320.jpg)







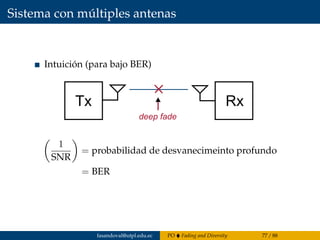
![¿Por qué el BER decrese con el número de las antenas
en recepción?
Para L antenas,
2L−1
C
L
1
2L
1
SNR
L
L = 1 →
1
2 · SNR
∝
1
SNR
L = 2 →
2
4
1
SNR
2
∝
1
SNR2
L = 3 → BER ∝
1
SNR3 −10 −5 0 5 10 15 20 25 30 35 40
10
−4
10
−3
10
−2
10
−1
10
0
Pout
10log
10
(γ/γ
0
)
M = 1
M = 2
M = 3
M = 4
M = 10
M = 20
Figure 7.5: Pout for MRC with i.i.d. Rayleigh fading.
Rayleigh fading, where pγΣ (γ) is given by (7.16), it can be shown that [4, Chapter 6.3]
Pb =
∞
0
Q( 2γ)pγΣ (γ)dγ =
1 − Γ
2
M M−1
m=0
M − 1 + m
m
1 + Γ
2
m
, (7
where Γ = γ/(1 + γ). This equation is plotted in Figure 7.6. Comparing the outage probab
for MRC in Figure 7.5 with that of SC in Figure 7.2 or the average probability of error for MR
Figure 7.6 with that of SC in Figure 7.3 indicates that MRC has significantly better performance t
SC. In Section 7.7 we will use a different analysis based on MGFs to compute average error probab
under MRC, which can be applied to any modulation type, any number of diversity branches, and
Referencia: [Goldsmith, 2005]
Cuando incrementa el número de antenas en el receptor, el BER
decrese a una tasa mucho más rápida.
fasandoval@utpl.edu.ec PO Fading and Diversity 74 / 88](https://image.slidesharecdn.com/dfadinganddiversity-190219172211/85/Tema-4-Fading-and-diversity-83-320.jpg)


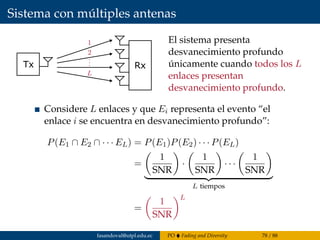



![Ejemplo: Separación de las antenas
Considere un sistema GSM con frecuencia portadora fc = 900 MHz. ¿Cuál es el
espaciamiento requerido entre antenas para contar con independencia de canales?
Solución:
λ =
c
fc
=
3 × 108[m/s]
900 × 106[1/s]
= 33.33 cm
Por lo tanto, el espaciamiento entre antenas es:
λ
2
=
33.33
2
= 16.66 cm
Nota: No es posible ubicar múltiples antenas en un celular.
fasandoval@utpl.edu.ec PO Fading and Diversity 81 / 88](https://image.slidesharecdn.com/dfadinganddiversity-190219172211/85/Tema-4-Fading-and-diversity-91-320.jpg)

![Ejemplo: Separación de las antenas
Ahora considere un sistema 3G/4G con frecuencia portadora fc = 2.3 GHz. ¿Cuál es
el espaciamiento requerido entre antenas para contar con independencia de canales?
Solución:
λ =
c
fc
=
3 × 108[m/s]
2.3 × 109[1/s]
= 13.04 cm
Por lo tanto, el espaciamiento entre antenas es:
λ
2
=
13.04
2
= 6.5 cm
Nota: Es posible ubicar múltiples antenas en un teléfono
3G/4G.
fasandoval@utpl.edu.ec PO Fading and Diversity 82 / 88](https://image.slidesharecdn.com/dfadinganddiversity-190219172211/85/Tema-4-Fading-and-diversity-93-320.jpg)





![Referencias I
Referencia Principal: [Jagannathan, 2013]
[Goldsmith, 2005] Goldsmith, A. (2005).
Wireless communications.
Cambridge university press.
[Jagannathan, 2013] Jagannathan (2013).
Advanced 3g and 4g wireless mobile communications.
[Tse and Viswanath, 2005] Tse, D. and Viswanath, P. (2005).
Fundamentals of wireless communication.
Cambridge university press.
[Wikipedia, 2016a] Wikipedia (2016a).
distribucion-x2.
https://es.wikipedia.org/wiki/Distribuci%C3%B3n_%CF%87%C2%B2.
[Online; accessed 27-Junio-2016].
[Wikipedia, 2016b] Wikipedia (2016b).
Teorema del limite central.
https://es.wikipedia.org/wiki/Teorema_del_l%C3%ADmite_central.
[Online; accessed 17-Junio-2016].
fasandoval@utpl.edu.ec PO Fading and Diversity 88 / 88](https://image.slidesharecdn.com/dfadinganddiversity-190219172211/85/Tema-4-Fading-and-diversity-99-320.jpg)