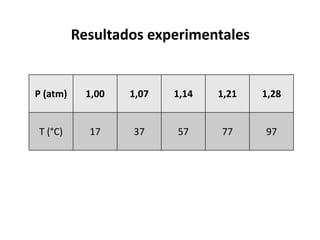
El documento describe un experimento que mide la relación entre la presión y la temperatura de un gas. Los resultados muestran que la presión y la temperatura no están directamente proporcionales cuando se usa la escala Celsius. Sin embargo, al cambiar a la escala Kelvin, donde el cero absoluto es 0 K, la presión y la temperatura están directamente proporcionales. Esto lleva a la Ley de Gay-Lussac, que establece que para un gas a volumen constante, la relación entre la presión y la temperatura es constante.

1. Ley de Gay-Lussac
Análisis de resultados experimentales

2. Resultados experimentales
P (atm) 1,00 1,07 1,14 1,21 1,28
T (°C) 17 37 57 77 97

3. Para estudiar la relación matemática representamos los datos gráficamente
0
0.2
0.4
0.6
0.8
1
1.2
1.4
0 20 40 60 80 100 120
P (atm)
T (⁰C)

4. Para estudiar la relación matemática representamos los datos gráficamente
0
0.2
0.4
0.6
0.8
1
1.2
1.4
0 20 40 60 80 100 120
P (atm)
T (⁰C)

5. Análisis de la gráfica
• No existe proporcionalidad directa entre P y T: “doble de
T no significa doble de P” (P/T NO es constante)
• Es una recta que no pasa por el origen de coordenadas.
Es decir, cuando T=0 la presión es distinta de cero: P≠0
• Significado físico: cuando T=0 ⁰C las moléculas siguen
moviéndose y golpeando a cualquier superficie…
¡todavía pueden ir más lentas!
• Para transformar esa gráfica en una recta que pasa por el
origen de coordenadas (proporcionalidad directa),
haremos un cambio de escala para que se cumpla: T=0
cuando P=0

6. Prolongamos la recta para ver cuándo corta al eje de T
0
0.2
0.4
0.6
0.8
1
1.2
1.4
-300 -200 -100 0 100 200
P (atm)
T (⁰C)

7. Prolongamos la recta para ver cuándo corta al eje de T
0
0.2
0.4
0.6
0.8
1
1.2
1.4
-300 -200 -100 0 100 200
P (atm)
T (⁰C)-273

8. Cambiamos la escala de T para que se cumpla: T=0 cuando P=0
0
0.2
0.4
0.6
0.8
1
1.2
1.4
-300 -200 -100 0 100 200
P (atm)
T (⁰C)

9. Cambiamos la escala de T para que se cumpla: T=0 cuando P=0
0
0.2
0.4
0.6
0.8
1
1.2
1.4
-300 -200 -100 0 100 200
P (atm)
T (⁰C)
0 T (K)

10. Cambiamos la escala de T para que se cumpla: T=0 cuando P=0
0
0.2
0.4
0.6
0.8
1
1.2
1.4
-300 -200 -100 0 100 200
P (atm)
T (⁰C)
0 17373 273 373 T (K)

11. Conclusiones:
• Definimos una nueva escala de temperatura, escala
Kelvin o absoluta, que se relaciona con la escala Celsius o
centígrada: T(K) = T(⁰C) + 273
• En esta nueva escala, la gráfica P-T será una recta que
pasa por el origen dando lugar a una proporcionalidad
directa, es decir: “doble T produce doble P”.
• En esa nueva escala, T=0 K significa que las moléculas se
encontrarían en reposo Inalcanzable), de forma que P=0
• Se llama escala absoluta de temperatura porque la
temperatura será siempre positiva.

12. Resultados experimentales (en Kelvin)
P (atm) 1,00 1,07 1,14 1,21 1,28
T (°C) 17 37 57 77 97
T (K) 290 310 330 350 370

13. 0
0.2
0.4
0.6
0.8
1
1.2
1.4
0 50 100 150 200 250 300 350 400
P (atm)
T (K)
Para estudiar la relación matemática representamos los datos gráficamente

14. Los puntos experimentales…
0
0.2
0.4
0.6
0.8
1
1.2
1.4
0 50 100 150 200 250 300 350 400
P (atm)
T (K)

15. Extrapolamos: recta que pasa por el origen, P/T = constante
0
0.2
0.4
0.6
0.8
1
1.2
1.4
0 50 100 150 200 250 300 350 400
P (atm)
T (K)

16. En este ejemplo concreto, esa constante vale:
1/290 = 0,0034 atm/K
pero ese valor depende del valor de las variables que
hemos controlado (volumen, masa…)

17. Ley de Gay-Lussac
Para una masa determinada de gas contenida en un
volumen constante, si:
P1 es la presión cuando la temperatura es T1
P2 es la presión cuando la temperatura es T2
se cumple:
P1/T1 = P2/T2
¡Pero T tiene que estar expresada en Kelvin!