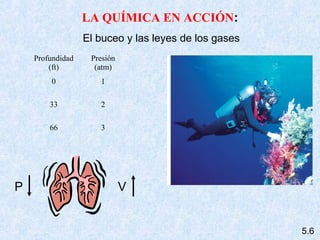
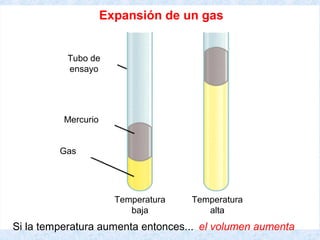
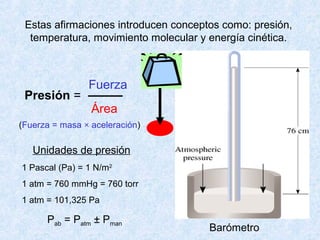
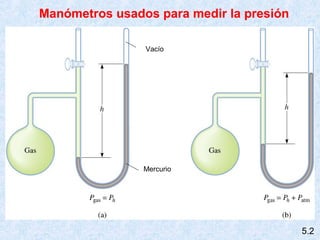
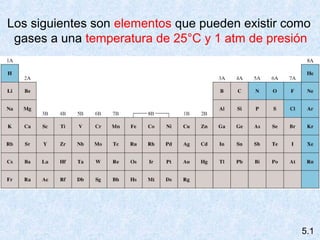
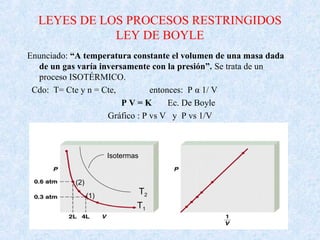
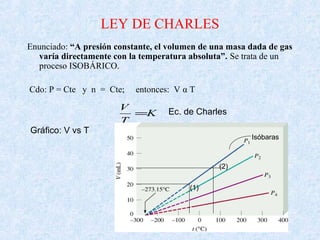
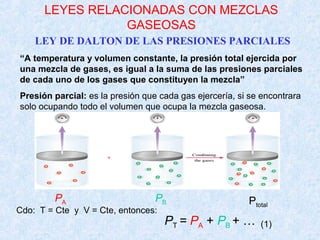
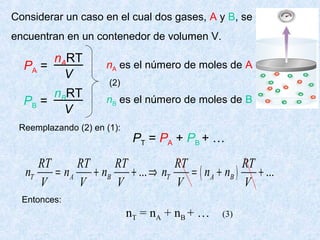
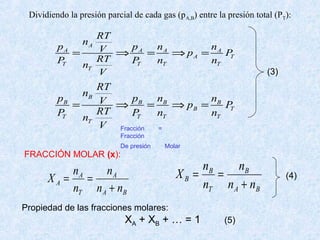
Este documento trata sobre los gases y sus propiedades físicas. Explica que los gases pueden adoptar cualquier forma, son compresibles y se expanden fácilmente. Además, presenta las leyes de Boyle, Charles y Gay-Lussac, las cuales describen la relación entre la presión, volumen y temperatura de los gases ideales. Finalmente, introduce la ecuación de estado de los gases ideales.

1. GASES
GASES IDEALES
Dr. Edson Yupanqui Torres

2. • Son capaces de adquirir cualquier forma, ocupan todo el volumen de sus
recipientes.
• Son compresibles y también se expanden.
• Pueden mezclarse con todo tipo de elementos con mucha facilidad
• Tienen una densidad mucho menor que los sólidos y los líquidos.
CARACTERÍSTICAS FÍSICAS DE LOS GASES
ESTADO GASEOSO
Los gases se pueden considerar como el más fascinante entre los tres estados de
agregación de la materia.

3. Si la temperatura aumenta entonces... el volumen aumenta
Temperatura
baja
Temperatura
alta
Gas
Mercurio
Expansión de un gas
Tubo de
ensayo

4. CLASIFICACIÓN DE LOS GASES
GASES IDEALES
. Se dan a presiones bajas y
temperaturas elevadas,
condiciones que corresponden a
grandes volúmenes molares.
. Se desprecia el volumen de la
molécula gaseosa.
. No sufren atracciones ni
repulsiones entre sus moléculas.
. No se condensan.
. Tienden a un volumen cero.
GASES REALES
. Se dan a presiones altas y
temperaturas bajas, condiciones
que corresponden a pequeños
volúmenes molares.
. Se considera el volumen de la
molécula gaseosa.
. Sufren atracciones y repulsiones
entre sus moléculas.
. Se condensan.
. No alcanzan un volumen igual a
cero, por que se licuefactan, es
decir pasan de gas a líquido.

5. TEORÍA CINÉTICO MOLECULAR DE LOS GASES
IDEALES
1. Un gas se compone de moléculas separadas una de la otra por
distancias más grandes que sus propias dimensiones. Dichas
moléculas pueden ser consideradas gráficamente como puntos; es
decir, su volumen puede ser despreciable.
2. Las moléculas de los gases siempre están en un continuo
movimiento desordenado y chocando en todas direcciones unas con
otras. Los choques entre las moléculas del gas son perfectamente
elásticos.
3. Las moléculas de los gases no ejercen fuerzas de atracción o
repulsión entre ellas.
4. La energía cinética promedio de las moléculas del gas es
directamente proporcional a su temperatura absoluta. Cualquier
gas a la misma temperatura tiene la misma energía cinética.

6. Unidades de presión
1 Pascal (Pa) = 1 N/m2
1 atm = 760 mmHg = 760 torr
1 atm = 101,325 Pa
Barómetro
Presión =
Fuerza
Área
(Fuerza = masa × aceleración)
Estas afirmaciones introducen conceptos como: presión,
temperatura, movimiento molecular y energía cinética.
Pab = Patm ± Pman

7. 5.2
Manómetros usados para medir la presión
Mercurio
Vacío

8. Los siguientes son elementos que pueden existir como
gases a una temperatura de 25°C y 1 atm de presión
5.1

9. 5.1
Elementos que existen como gases a una temperatura de 25°C y 1 atm de presión

10. LEYES DE LOS PROCESOS RESTRINGIDOS
LEY DE BOYLE
Enunciado: “A temperatura constante el volumen de una masa dada
de un gas varía inversamente con la presión”. Se trata de un
proceso ISOTÉRMICO.
Cdo: T= Cte y n = Cte, entonces: P α 1/ V
P V = K Ec. De Boyle
Gráfico : P vs V y P vs 1/V
T1
T2
Isotermas
(1)
(2)

11. En el punto (1) : P1 x V1 = K
En el punto (2) : P2 x V2 = K
Igualando ambas ecuaciones:
P1 x V1 = P2 x V2
Ordenando:
1
2
2
1
V
V
P
P
=






=
m
m
V
P
V
P
1
2
2
1






=





1
2
2
1
V
m
P
V
m
P
A menor P mayor V
A mayor P menor V
En función de la densidad (ρ):
Si: ρ = m / V
Entonces: P1 x ρ2 = P2 x ρ1
2
1
2
1
ρ
ρ
=
P
P

12. Una muestra de cloro en estado gaseoso ocupa un
volumen de 946 mL y se encuentra a una presión de
726 mmHg. ¿Cuál es la presión que se necesita para
que el volumen disminuya a 154 mL si la temperatura
de la muestra es constante?
P1 x V1 = P2 x V2
P1 = 726 mmHg
V1 = 946 mL
P2 = ?
V2 = 154 mL
P2 =
P1 x V1
V2
726 mmHg x 946 mL
154 mL
= = 4460 mmHg
P x V = constante

13. LEY DE CHARLES
Enunciado: “A presión constante, el volumen de una masa dada de gas
varía directamente con la temperatura absoluta”. Se trata de un
proceso ISOBÁRICO.
Cdo: P = Cte y n = Cte; entonces: V α T
K
T
V
= Ec. de Charles
Gráfico: V vs T
(1)
(2)
Isóbaras

14. En el punto (1) : V1 / T1 = K
En el punto (2) : V2 / T2 = K
Igualando:
2
2
1
1
T
V
T
V
=
2
1
2
1
T
T
V
V
=






=
m
m
V
T
V
T
2
2
1
1
Ordenando: A menor T menor V
A mayor T mayor V
En función de la densidad: ρ






=





2
2
1
1
V
m
T
V
m
T Si: ρ = m/V
Entonces: T1x ρ1 = T2 x ρ2
1
2
2
1
ρ
ρ
=
T
T

15. Una muestra de monóxido de carbono en estado
gaseoso se encuentra a una temperatura de 125°C. Si
el volumen inicial de la muestra es de 3,2 litros, ¿Qué
temperatura debe tener el sistema si se quiere reducir
el volumen a 1,54 litros, si la presión es constante?
V1 = 3,20 L
T1 = 398,15 K
V2 = 1,54 L
T2 = ?
T2 =
V2 x T1
V1
1,54 L x 398,15 K
3,20 L
= = 192 K
5.3
V1 /T1 = V2 /T2
T1 = 125 (0
C) + 273,15 (K) = 398,15 K

16. LEY DE GAY-LUSSAC
Enunciado: “A volumen constante la presión ejercida por una masa dada de gas
varía directamente con la temperatura absoluta”. Se trata de un proceso
ISOCÖRICO o ISOMËTRICO.
Cdo: V = Cte y n = Cte, entonces: P α T
Luego: P = K x T
K
T
P
= Ec. De Gay-Lussac
Gráfico: P vs T
P
T
(1)
(2)
Isócoras
V1
V2
V3
T
T1 T2
P1
P2

17. En el punto (1) : P1 / T1 = K
En el punto (2) : P2 / T2 = K
Igualando:
2
2
1
1
T
P
T
P
=
A menor T menor P
A mayor T mayor P
Ordenando:
2
1
2
1
T
T
P
P
=

18. El aire en un tanque se encontraba a una presión de 620 mm Hg y 23 ºC.
S e expuso al sol con lo que su temperatura aumentó a 50 ºC. ¿Cuál fue
la presión que presentó entonces el tanque?.
SOLUCIÓN
Datos
Condición (1)
P1 = 620 mm Hg
T1 = 23 ºC + 273 = 296 ºK
Condición (2)
T2 = 50 ºC + 273 = 323 ºK
P2 = ?
1
21
2
2
1
2
1
T
TP
P
T
T
P
P ×
=⇒=
Como el V = Cte y n = Cte
La fórmula a usar es:
(1)
Reemplazando valores en (1):
K
KmmHg
P
º296
º323630
2
×
=
P2 = 676,55 mm Hg

19. El argón es un gas inerte que se usa en algunas
bombillas para retrasar la vaporización del filamento.
Cierto foco contiene argón a 1,2 atm de presión y
cambia de temperatura desde 18°C hasta 85°C. ¿Cuál
es la presión final del argón en atm si el volumen del
sistema es constante?
P1
T1
P2
T2
=
P2 = P1 x
T2
T1
= 1,20 atm x 358 K
291 K
= 1,48 atm
SOLUCIÓN
Condición inicial(1)
P1 = 1,2 atm
T1 = 18ºC + 273 = 291 K
Condición final (2)
P2 = ?
T2 = 85ºC + 273 = 358 K
(Ley de Gay-Lussac)

20. LEY DE AVOGADRO
Enunciado: “A presión y temperatura constante el volumen de un gas es
directamente proporcional al número de moles del gas”.
Cdo: P = Cte y T = Cte, entonces: V α n
Luego: V = K x n
Entonces:
K
n
V
= Ec. De Avogadro
Gráfico: V vs n
V
n
(1)
(2)
n1 n2
V2
V1

21. En el punto (1) : V1 / n1 = K
En el punto (2) : V2 / n2 = K
Igualando:
2
2
1
1
n
V
n
V
=
2
1
2
1
n
n
V
V
=






=





⇒





=
2
2
1
1
2
2
1
1
V
m
n
V
m
n
m
m
V
n
V
n
Ordenando
A mayor n mayor V
A menor n menor V
En función de la densidad: ρ
Si: ρ = m / V
1
2
2
1
2211
ρ
ρ
ρρ =⇒×=×
n
n
nnFinalmente:

22. ECUACIÓN DE ESTADO DE LOS GASES
IDEALES
Una ecuación que relaciona la temperatura, presión, volumen moles o masa de una
sustancia gaseosa, recibe el nombre de ecuación de estado. Relacionando las
siguientes leyes:
Ley de Boyle: V α 1 / P (T y n constantes)
Ley de Charles: V α T (P y n constantes)
Ley de Avogadro : V α n (T y P constantes)
Entonces:
P
TnR
V
P
Tn
V
××
=⇒
×
α
Donde: PV = nRT (1)
Si: n = m / M, entonces: PVM = mRT (2)
Si: ρ = m / V, entonces: PM = ρRT (3)

23. Cuando en una muestra la temperatura es 0°C y la
presión es 1 atm, se dice que ésta se encuentra en
condiciones normales de presión y temperatura.
Se ha demostrado que en condiciones normales
de presión y temperatura, 1 mol de un gas ideal
ocupa 22,414 litros de volumen.
CONDICIONES NORMALES (CN O PTN)
Cuando:
P = 1 atm
T = 0 ºC = 273 ºK
Entonces:
1 mol-g gas a CN = 22,414 L
1 mol-kg gas a CN = 22,414 m3
1 mol-lb gas a CN = 359 pies3

24. VALORES DE LA CONSTANTE
UNIVERSAL DE LOS GASES: R
Los valores de “R”, se obtienen de la ecuación (1): PV = nRT, a
condiciones normales.
Kmol
atmL
Kmol
Latm
Tn
VP
R
º
082056,0
º15,2731
414,221
×
×
=
×
×
=
×
×
=
Otros valores de
“R”:
Kmol
mmHgL
R
º
36,62
×
×
=
Kmol
dmKPa
R
º
314,8
3
×
×
=
Rlbmol
piepulb
R
º
lg/
73,10
32
×−
×
=

25. ¿Cuál es el volumen en litros que ocupan 49,8 gramos
de ácido clorhídrico (HCL) a presión y temperatura
normales?
PV = nRT
V =
nRT
P
T = 0 0
C = 273,15 K
P = 1 atm
n = 49,8 g x
1 mol HCl
36,45 g HCl
= 1,37 mol
V =
1 atm
1,37 mol x 0,0821 x 273,15 KL•atm
mol•K
V = 30,6 L

26. Un contenedor de 2,1 litros contiene 4,65 gramos de
un gas a 1 atm de presión a 27°C. ¿Cuál es la
molaridad del gas?
dRT
P
M =
d = m
V
4,65 g
2,10 L
= = 2,21
g
L
M =
2,21
g
L
1 atm
x 0,0821 x 300,15 KL•atm
mol•K
M = 54,6 g/mol

27. LEY GENERAL O COMBINADA DE LOS GASES
En una ley general de los gases intervienen las tres variables: temperatura,
presión y volumen, para un sistema cerrado a condición inicial (1) y
final (2):
Estado inicial (1) : P1V1 = nRT1
Estado final (2) : P2V2 = nRT2
Dividiendo (1) entre (2): si, n = Cte y R = Cte.
2
1
22
11
2
1
22
11
T
T
VP
VP
TRn
TRn
VP
VP
=
×
×
⇒
××
××
=
×
×
Finalmente:
2
22
1
11
T
VP
T
VP ×
=
×
En función de las densidades: ρ (1) y (2):
12
21
2
1
TP
TP
×
×
=
ρ
ρ

28. Un litro de oxígeno tiene una masa de 1,43 g a 0ºC y a 760 mm Hg.
Calcular la densidad del oxígeno a 25ºC y 725 mm Hg.
SOLUCIÓN
Condiciones iniciales (1)
ρ1 = 1,43 g/L
T1 = 0ºC + 273= 273 ºK
P1 = 760 mm Hg
Condiciones finales (2)
ρ2 = ?
T2 = 25ºC + 273 = 298 ºK
P2 = 725 mm Hg
12
21
2
1
TP
TP
×
×
=
ρ
ρ
La fórmula es:
(1)
Reemplazando valores en (1):
KmmHg
KmmHgLg
TP
TP
º298760
º273725/43,1
2
21
121
2
×
××
=⇒
×
××
= ρ
ρ
ρ
ρ2 = 1,25 g/L

29. LEY DE DALTON DE LAS PRESIONES PARCIALES
PA PB
PT = PA + PB + …
LEYES RELACIONADAS CON MEZCLAS
GASEOSAS
“A temperatura y volumen constante, la presión total ejercida por
una mezcla de gases, es igual a la suma de las presiones parciales
de cada uno de los gases que constituyen la mezcla”
Presión parcial: es la presión que cada gas ejercería, si se encontrara
solo ocupando todo el volumen que ocupa la mezcla gaseosa.
Cdo: T = Cte y V = Cte, entonces:
Ptotal
(1)

30. Considerar un caso en el cual dos gases, A y B, se
encuentran en un contenedor de volumen V.
PA =
nART
V
PB =
nBRT
V
nA es el número de moles de A
nB es el número de moles de B
PT = PA + PB + …
(2)
Reemplazando (2) en (1):
( )... ...T A B T A B
RT RT RT RT RT
n n n n n n
V V V V V
= + + ⇒ = + +
Entonces:
nT = nA + nB + … (3)

31. Dividiendo la presión parcial de cada gas (pA,B) entre la presión total (PT):
A
A A A A
A T
T T T T
T
RT
n
p p n nV p P
RTP P n nn
V
= ⇒ = ⇒ =
B
B B B B
B T
T T T T
T
RT
n
p p n nV p P
RTP P n nn
V
= ⇒ = ⇒ =
BA
A
T
A
A
nn
n
n
n
X
+
==
(3)
FRACCIÓN MOLAR (x):
Fracción =
Fracción
De presión Molar
BA
B
T
B
B
nn
n
n
n
X
+
==
Propiedad de las fracciones molares:
XA + XB + … = 1 (5)
(4)

32. Reemplazando (4) en (3), tenemos:
pA = XA x PT
pB = XB x PT
pC = XC x PT
Una muestra de gas natural contiene: 8,24 moles de CH4, 0,421 moles
de C2H6, y 0,116 moles de C3H8. Si la presión total de los gases es de
1,37 atm, ¿Cuál es la presión parcial del propano (C3H8)?
SOLUCIÓN
Datos
nA = 8,24 mol
nB = 0,421 mol
nC = 0,116 mol
PT = 1,37 atm
1º. Cálculo de XC ( propano) :
0132,0
116,0421,024,8
116,0
=
++
=
++
=
CBA
C
C
nnn
n
X
2º. Cálculo de la presión parcial del propano: pC
pC = XC x PT = 0,0132 x 1,37 atm
pC = 0,0181 atm
(6)

33. 2KClO3 (s) 2KCl (s) + 3O2 (g)
Contenedor de oxígeno y
vapor de agua
RECOLECCIÓN DE GASES SOBRE LÍQUIDOS
Es una de la aplicación más útil de la Ley de Dalton, en los que intervienen la
colección de los gases sobre agua, donde el vapor de agua se encuentra presente
mezclados con los gases colectados. En dichos cálculos debe hacerse una
corrección por el vapor de agua presente.
Rx qca de desprendimiento de gas
Donde:
PT = Pgh = PO2 + PVH2O
Generalizando:
PT = Pgh = Pgs + PvH2O
Pgs = Pgh – PvH2O
Cdo: Pgh = PT = Patm
Patm = Pgh = PT = Pgs + PVH2O

34. RECOLECCIÓN DE HIDRÓGENO EN AGUA

35. PRESIÓN DE VAPOR DEL AGUA

36. Se recibió 0,0052 moles de H2 (g) sobre agua a 27ºC y 807 mm Hg. Calcule el
volumen que ocupará el hidrógeno. Si PvH2O (27ºC) = 27 mm Hg.
SOLUCIÓN
T = 27ºC + 273 = 300 K
Pgh = 807 mm Hg
V = ?
n = 0,0052 mol
PvH2O (27ºC) = 27 mm Hg.
Fórmula:
Pgh = Pgs + PvH2O
Pgs = Pgh – PvH2O
Pgs = 807 mm Hg – 27 mm Hg
Pgs = 780 mm Hg.
Cálculo del volumen de H2 (g):
PV = nRT
mLL
mmHg
K
Kmol
LmmHg
mol
P
TRn
V 1251248,0
780
3004,620052,0
==
×
×
×
×
=
××
=

37. HUMEDAD RELATIVA: Hr
Es el contenido de vapor de agua que contiene el gas.
%100%
2
2
×=
OvH
OH
P
p
Hr
pH2O = Presión parcial del agua gaseosa
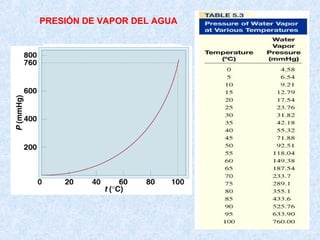
PvH2O = Presión de vapor o tensión de vapor del agua en equilibrio con
su líquido (tablas)
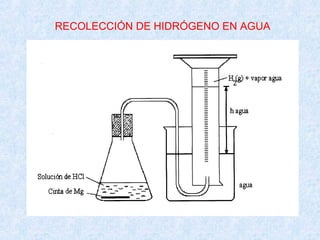
¿Cuántos miligramos de vapor de agua contiene un frasco de 2L lleno
de aire al 70% de humedad y a 25ºC?. Si PvH2O (25ºC) = 23,76 mm Hg.
SOLUCIÓN
m= ? H2O
V = 2 L
%Hr = 70%
T = 25ºC + 273 = 298 K
PvH2O (25ºC) = 23,76 mm Hg
Por fórmula: %Hr= (pH2O / PvH2O) x 100%
70% = (pH2O / 23,76 mmHg) x 100%
pH2O = 16,6 mmHg
Cálculo del V:
PVM = mRT, entonces : m = (MPV)/
RTm = [18 g/mol x 16,6 mmHg x 2 L] / [62,4 (mmHg x L / mol x K) x 298 K]
m = 0,03213 g = 32,13 mg

38. LEY DE AMAGAT O LEY DE LOS
VOLUMENES PARCIALES
Enunciado: “A temperatura y presión constante, el volumen total ocupado
por una mezcla gaseosa es igual a la suma de los volúmenes parciales de sus
gases componentes”.
Volumen parcial (v): es el volumen que ocupará aquel componente gaseoso si el
solo estuviera presente a la misma temperatura y presión que tiene la mezcla.
Cdo: T = Cte y P = Cte, VT = vA + vB + … (1)
Si: VT = nTRT/ P ; vA = nART/P vB = nB RT/ P (2)
Reemplazando (2) en (1):
nTRT/ P = nART/ P + nBRT/ P + …
nTRT/ P = (nA + nB + …) RT/ P
Entonces:
nT = nA + nB + … (3)

39. Dividiendo el volumen parcial (vA,B) entre el volumen total (VT):
T
T
A
A
T
A
T
A
T
A
T
A
V
n
n
v
n
n
V
v
P
RT
n
P
RT
n
V
v
×=⇒=⇒=
B
B B B B
B T
T T T T
T
RT
n
v v n nP v V
RTV V n nn
P
= ⇒ = ⇒ = ×
A A
A
T A B
n n
X
n n n
= =
+ BA
B
T
B
B
nn
n
n
n
X
+
==
FRACCIÓN MOLAR (X)
(4)
(5)
Propiedad de las fracciones molares:
XA + XB + … = 1 (6)
Fracción de = Fracción
Volumen molar

40. Reemplazando (5) en (4):
vA = XA x VT
vB = XB x VT
vC = XC x VT
A
B
A
B
B
A
M
M
ρ
ρ
µ
µ
==
(7)
LEY DE GRAHAM DE LA DIFUSIÓN GASEOSA
“A presión y temperatura constante las velocidades de difusión de
dos gases diferentes son inversamente proporcionales a las raíces
cuadradas de sus masa moleculares o densidades”
Se sabe que:
μ = V / t (2) o μ= d / t (3)
(1)
A
B
A
B
B
A
B
A
M
M
d
d
V
V
ρ
ρ
===Cdo: tA = tB, se tiene: (4)
P = Cte
T = Cte

41. Dos globos del mismo tamaño y material se llenan respectivamente con hidrógeno
y oxígeno gaseoso a la misma temperatura y presión. Si el oxígeno escapa con una
rapidez de 65 mL/h. Calcular la rapidez con que escapará el hidrógeno.
SOLUCIÓN
Datos
μO2 = 65 mL/h
μH2 = ?
O2 → M = 32 g/mol
H2 → M = 2 g/mol
molg
molg
hmL
M
M
M
M
H
O
OH
H
O
O
H
/2
/32
/65
2
2
22
2
2
2
2
==⇒= µµ
µ
µ
μH2 = 260 mL / h

42. LA QUÍMICA EN ACCIÓN:
El buceo y las leyes de los gases
P V
Profundidad
(ft)
Presión
(atm)
0 1
33 2
66 3
5.6

43. GASES REALES
Gas ideal
PV / RT= 1
Fuerzas de repulsión
Fuerzas de atracción
Gas ideal
Gas real
PV / RT ≠ 1
PV / RT = Z
Entonces:
Z = 1→ Gas ideal
Z ≠ 1 → Gas real
Luego:
PV = ZRT → n = 1 mol
PV = ZnRT → “n” moles
Z = Factor de compresibilidad

44. Demostración del efecto de las fuerzas de presión
producidas por un gas (atracciones y repulsiones
moleculares
5.8

45. Ecuación de Van der Waals
para gases reales
P + (V – nb) = nRTan2
V2( )
}
Presión
corregida
}
Volumen
corregido

46. GRACIAS POR SU ATENCIÓN