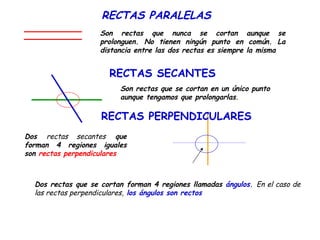
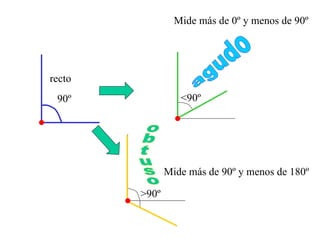
El documento describe conceptos básicos de geometría como rectas, puntos, segmentos, semirrectas y ángulos. Explica que una recta es una línea continua sin curvas ni ángulos, y que un punto divide una recta en dos semirrectas. Describe rectas paralelas, secantes y perpendiculares. Define un ángulo y sus elementos, y clasifica ángulos en rectos, agudos y obtusos. También cubre ángulos complementarios, suplementarios y adyacentes, y cómo medir y dibujar ángulos.

1. GEOMETRIA RECTAS ÁNGULOS

2. Rectas Una recta es una línea continua de puntos, sin curvas ni ángulos, que no tiene principio ni fin PUNTO SEMIRRECTAS Un punto divide a una recta en dos semirrectas que son también líneas de puntos, sin curvas ni ángulos, con principio pero sin fin. El punto es el origen de cada una. Un segmento es una parte de la recta limitada por dos puntos, es decir con principio y fin EXTREMOS SEGMENTO

3. RECTAS PARALELAS Son rectas que nunca se cortan aunque se prolonguen. No tienen ningún punto en común. La distancia entre las dos rectas es siempre la misma RECTAS SECANTES Son rectas que se cortan en un único punto aunque tengamos que prolongarlas . Dos rectas secantes que forman 4 regiones iguales son rectas perpendiculares Dos rectas que se cortan forman 4 regiones llamadas ángulos. En el caso de las rectas perpendiculares, los ángulos son rectos RECTAS PERPENDICULARES

4. Ángulos Ángulos

5. A B D C Vamos a unir estas dos semirrectas. Obtenemos lo que se llama “ángulo” Ángulo es la región del plano comprendida entre dos semirrectas (lados) que se unen en un punto ( vértice ). A B C â lado lado vertice

6. Los elementos de un ángulo son: Lados: son dos semirrectas que forman los bordes del ángulo Vértice: es el punto donde se cortan los lados Amplitud: es la abertura de los lados Dos rectas perpendiculares forman 4 regiones iguales, y cada una de ellas determina un ángulo recto Ángulo recto= 90º

7. CLASIFICACIÓN DE LOS ÁNGULOS

8. 90º El ángulo formado por dos rectas perpendiculares se llama: ángulo recto

9. 90º <90º >90º recto agudo obtuso Mide más de 0º y menos de 90º Mide más de 90º y menos de 180º

10. Otros ángulos: nulo 0º

11. Otros ángulos: llano 180º

12. Otros ángulos: 270º

13. Otros ángulos: 270º completo 360º

14. e Otros ángulos: Todo ángulo divide al plano en dos regiones. < 180º > 180º

15. e Otros ángulos: Todo ángulo divide al plano en dos regiones. < 180º > 180º Ángulo cóncavo Ángulo convexo

16. Clasificación de ángulos EL ANGULO COMPLETO tiene una amplitud equivalente a 4 ángulos rectos, 360º

17. Los ángulos ,según el vértice y los lados, pueden ser: A) Ángulos consecutivos Lado común 35º 50º Comparten un lado y un vértice. La medida del ángulo que forman es la suma de los dos ángulos 35º + 50º = 85º

18. B) Ángulos opuestos por el vértice Comparten el vértice y los lados de uno son prolongación del otro Son ángulos iguales Mismo vértice

19. Dos ángulos ,según el resultado de su suma, pueden ser: A) Ángulos complementarios Dos ángulos complementarios suman 90º 30º 60º 30º + 60º= 90º

20. B) Ángulos suplementarios Dos ángulos suplementarios suman 180º 60º 120º 60º + 120º= 180º

21. Suman 180º ÁNGULOS ADYACENTES Son ángulos consecutivos cuyos lados no comunes están en línea recta. Los ángulos adyacentes son suplementarios, porque juntos equivalen a un ángulo llano (180º).

22. ¿Cómo se miden los ángulos? Necesitamos una herramienta: llamada transportador , que es un semicírculo graduado de 0º a 180º, generalmente tiene dos escalas. 0 180 180 0 â

23. ¿Cómo se miden los ángulos? Colocamos el punto central del transportador sobre el vértice del ángulo. â De forma que uno de los dos lados salga por un 0. 0 Continuando por la escala de ese cero seguimos hasta encontrar el otro lado. 50 El ángulo â = 50º

24. 180 0 Colocamos el punto central del transportador sobre el vértice del ángulo. De forma que uno de los dos lados salga por un 0. ¿Cómo se miden los ángulos? Continuamos por esa escala hasta encontrar el otro lado. El ángulo â = 135º â gvwerbgwerwsrbwsrwrbwrbwrwrbwrwrwsrbwrwbwwrbwrbwwwrwrgbwrg

25. ¿Cómo se dibujan los ángulos? 1º.- Dibujamos una semirrecta y señalamos el vértice donde queremos colocar el ángulo. Dibuja un ángulo de 150º 2º.- Situamos el centro del semicírculo en el vértice señalada, haciendo coincidir la semirrecta con uno de los dos ceros. 3º.- Buscamos los 150 º en la escala del cero. 4º.- Marcamos en el papel ese punto y trazamos el otro lado.

28. Expresa en minutos: 34º 15’ 34º= 34 X 60= 2.040 ‘ 2.040’ + 15’= 2.055’ El ángulo mide 2.055’ Expresa en segundos: 15º 25’ 36’’ 15º= 15x60= 900’ 900’ + 25 ‘= 925’ 925’= 925x60= 55.500’’ 55.500’’ + 36’’= 55.536’’ El ángulo mide 55.536’’

29. ¿Cuántos grados son 12.525’’? 1´= 60´´ 1º= 60´

37. Suma de los ángulos de un triángulo y un cuadrilátero La suma de los ángulos de un triángulo es igual a 180º. Comprueba que aunque las medidas de los ángulos de los triángulos son distintas, la suma de los ángulos de todos ellos siempre es igual a 180º. La suma de los ángulos de un cuadrilátero es igual a 360º. Comprueba que aunque las medidas de los ángulos de los cuadriláteros cambian, la suma de los ángulos de todos ellos siempre es igual a 360º.