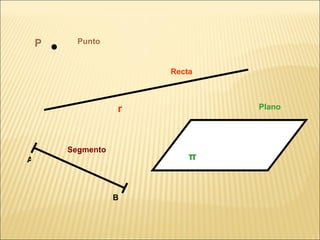
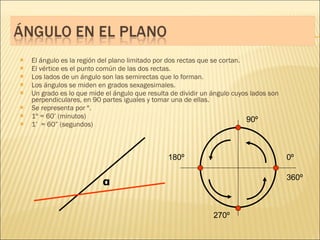
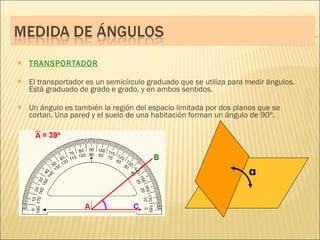
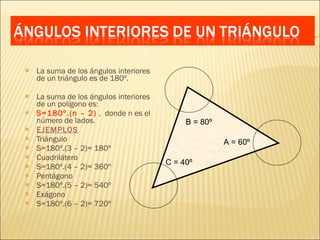
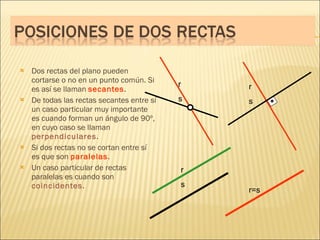
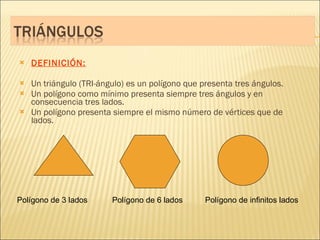
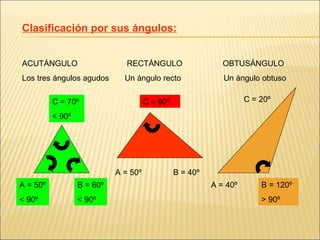
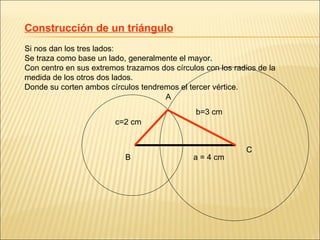
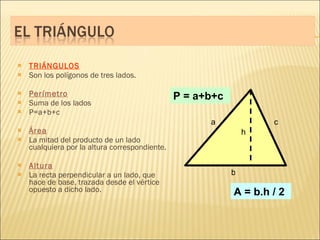
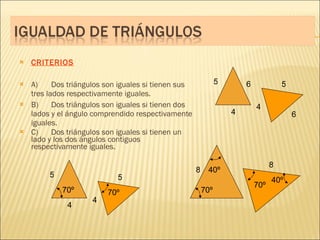
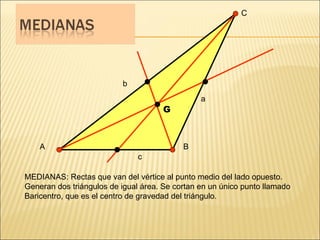
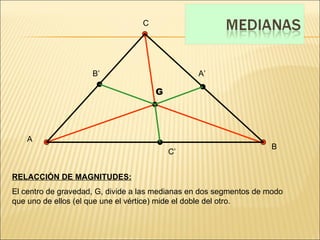
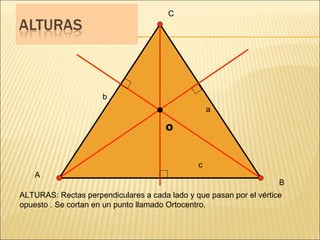
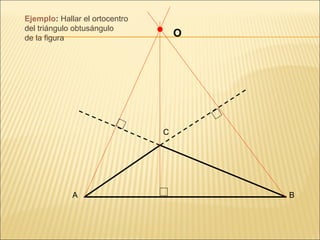
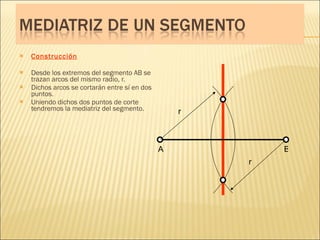
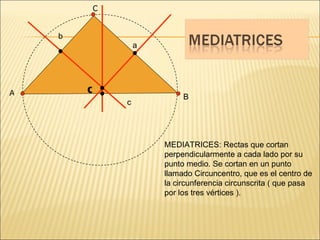
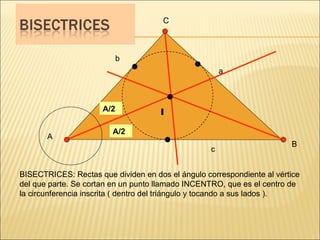
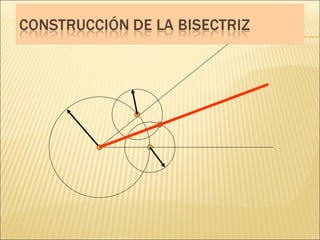
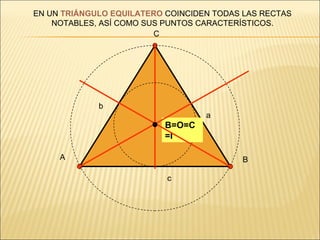
El documento describe conceptos básicos de geometría como el punto, la recta, el plano y el ángulo. Explica las diferentes clasificaciones de triángulos según sus lados y ángulos. También describe las rectas notables en un triángulo como las medianas, alturas y bisectrices y los puntos donde se cortan.

1. Ideas y conceptos previos Grupo cinco

2. PUNTO El punto es la entidad básica de geometría. Carece de dimensiones, es decir no tiene largo, ni ancho ni espesor. Es el lugar de la recta, del plano o del espacio al que es posible asignar una posición. RECTA La recta se puede definir como la sucesión de puntos alineados en una misma dirección. Tiene longitud, pero no tiene ni anchura ni espesor. SEMIRECTA Una semirecta es cada una de las dos partes en que queda dividida una recta por un punto. Tiene principio, pero no fin. SEGMENTO Es la parte de una recta limitada por dos puntos, A y B. Se representa por AB. PLANO Es una superficie tal que una recta que tenga dos puntos comunes con ella está contenida totalmente en la misma.

3. Punto Recta Plano P r π Segmento A B

4. El ángulo es la región del plano limitado por dos rectas que se cortan. El vértice es el punto común de las dos rectas. Los lados de un ángulo son las semirectas que lo forman. Los ángulos se miden en grados sexagesimales. Un grado es lo que mide el ángulo que resulta de dividir un ángulo cuyos lados son perpendiculares, en 90 partes iguales y tomar una de ellas. Se representa por º. 1º = 60’ (minutos) 1’ = 60” (segundos) 0º 270º 180º 90º 360º α

5. TRANSPORTADOR El transportador es un semicírculo graduado que se utiliza para medir ángulos. Está graduado de grado e grado, y en ambos sentidos. Un ángulo es también la región del espacio limitada por dos planos que se cortan. Una pared y el suelo de una habitación forman un ángulo de 90º. α

6. ÁNGULOS Dos rectas perpendiculares forman un ángulo de 90º. Decimos entonces que forman un ángulo recto . Un ángulo es agudo si es menor de 90º Un ángulo es obtuso si es mayor de 90º Un ángulo es llano si su medida es de 180º. Un ángulo es completo si su medida es de 360º Un ángulo es convexo si su medida está entre 0º y 180º Un ángulo es cóncavo si medida está entre 180º y 360º

7. ÁNGULOS ENTRE SÍ Dos ángulos son COMPLEMENTARIOS si suman 90º. Dos ángulos son SUPLEMENTARIOS si suman 180º. Dos ángulos se llaman OPUESTOS POR EL VÉRTICE si tienen el vértice común y los lados de uno son prolongación de los lados del otro. α α α β β β α + β = 90º α + β = 180º α = β

8. La suma de los ángulos interiores de un triángulo es de 180º. La suma de los ángulos interiores de un polígono es: S=180º.(n – 2) , donde n es el número de lados. EJEMPLOS Triángulo S=180º.(3 – 2)= 180º Cuadrilátero S=180º.(4 – 2)= 360º Pentágono S=180º.(5 – 2)= 540º Exágono S=180º.(6 – 2)= 720º A = 60º B = 80º C = 40º

9. Dos rectas del plano pueden cortarse o no en un punto común. Si es así se llaman secantes . De todas las rectas secantes entre sí un caso particular muy importante es cuando forman un ángulo de 90º, en cuyo caso se llaman perpendiculares . Si dos rectas no se cortan entre sí es que son paralelas . Un caso particular de rectas paralelas es cuando son coincidentes . r s r s r s r=s

10. DEFINICIÓN: Un triángulo (TRI-ángulo) es un polígono que presenta tres ángulos. Un polígono como mínimo presenta siempre tres ángulos y en consecuencia tres lados. Un polígono presenta siempre el mismo número de vértices que de lados. Polígono de 3 lados Polígono de 6 lados Polígono de infinitos lados

11. Clasificación por sus lados: ESCALENO ISÓSCELES EQUILATERO 3 lados desiguales 2 lados iguales 3 lados iguales b = 4 a = 5 c = 6 b = 6 a = 6 c = 4 b = 4 a = 4 c = 4

12. Clasificación por sus ángulos: ACUTÁNGULO RECTÁNGULO OBTUSÁNGULO Los tres ángulos agudos Un ángulo recto Un ángulo obtuso A = 50º < 90º B = 60º < 90º C = 70º < 90º A = 50º B = 40º C = 90º C = 20º A = 40º B = 120º > 90º

13. Construcción de un triángulo Si nos dan los tres lados: Se traza como base un lado, generalmente el mayor. Con centro en sus extremos trazamos dos círculos con los radios de la medida de los otros dos lados. Donde su corten ambos círculos tendremos el tercer vértice. a = 4 cm b=3 cm c=2 cm A B C

14. TRIÁNGULOS Son los polígonos de tres lados. Perímetro Suma de los lados P=a+b+c Área La mitad del producto de un lado cualquiera por la altura correspondiente. Altura La recta perpendicular a un lado, que hace de base, trazada desde el vértice opuesto a dicho lado. h c b a P = a+b+c A = b.h / 2

15. CRITERIOS A) Dos triángulos son iguales si tienen sus tres lados respectivamente iguales. B) Dos triángulos son iguales si tienen dos lados y el ángulo comprendido respectivamente iguales. C) Dos triángulos son iguales si tienen un lado y los dos ángulos contiguos respectivamente iguales. 5 6 4 4 5 6 5 70º 4 4 5 70º 8 70º 40º 40º 8 70º

16. RECTAS NOTABLES EN UN TRIÁNGULO. MEDIATRICES .- Rectas perpendiculares a un lado y que pasan por el punto medio de dicho lado. Corte único de las mediatrices: CIRCUNCENTRO, que es el centro de la circunferencia que pasa por los tres vértices del triángulo. BISECTRICES .-Rectas que partiendo del vértice parten el ángulo en dos iguales. Corte único de bisectrices: INCENTRO, que es el centro de la circunferencia inscrita (interior), tangente a los tres lados. ALTURAS .- Rectas perpendiculares a los lados y que parten del vértice opuesto a cada uno de ellos. Corte único de alturas: ORTOCENTRO. MEDIANAS .- Rectas que van del vértice al punto medio del lado opuesto. Dividen el triángulo en dos regiones de igual área. Corte único de medianas: BARICENTRO, que es el centro de gravedad del triángulo (  Física).

17. A C B a c b MEDIANAS: Rectas que van del vértice al punto medio del lado opuesto. Generan dos triángulos de igual área. Se cortan en un único punto llamado Baricentro, que es el centro de gravedad del triángulo. G

18. A C B A’ C’ B’ RELACCIÓN DE MAGNITUDES: El centro de gravedad, G, divide a las medianas en dos segmentos de modo que uno de ellos (el que une el vértice) mide el doble del otro. G

19. A C B a c b ALTURAS: Rectas perpendiculares a cada lado y que pasan por el vértice opuesto . Se cortan en un punto llamado Ortocentro. O

20. A B C O Ejemplo : Hallar el ortocentro del triángulo obtusángulo de la figura

21. Construcción Desde los extremos del segmento AB se trazan arcos del mismo radio, r. Dichos arcos se cortarán entre sí en dos puntos. Uniendo dichos dos puntos de corte tendremos la mediatriz del segmento. r r A B

22. B MEDIATRICES: Rectas que cortan perpendicularmente a cada lado por su punto medio. Se cortan en un punto llamado Circuncentro, que es el centro de la circunferencia circunscrita ( que pasa por los tres vértices ). A C a c b C

23. A C B a c b BISECTRICES: Rectas que dividen en dos el ángulo correspondiente al vértice del que parte. Se cortan en un punto llamado INCENTRO, que es el centro de la circunferencia inscrita ( dentro del triángulo y tocando a sus lados ). I A/2 A/2

25. EN UN TRIÁNGULO EQUILATERO COINCIDEN TODAS LAS RECTAS NOTABLES, ASÍ COMO SUS PUNTOS CARACTERÍSTICOS. A C B a c b B=O=C=I