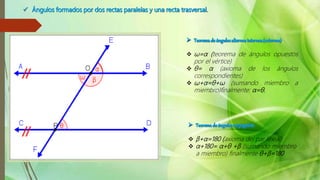
Este documento describe diferentes tipos de ángulos y sus propiedades. Explica ángulos adyacentes, opuestos por el vértice, correspondientes y complementarios. También cubre teoremas relacionados con estas propiedades angulares como el teorema de ángulos opuestos por el vértice y el axioma de ángulos correspondientes. El documento concluye que es importante conocer los diferentes tipos de ángulos que se usan comúnmente.

1. .

2. Al termino de la sesión, es estudiante tendrá la
capacidad de diferenciar los distintos tipos de
ángulos, y aplicar en los ejercicios.

3. Es una figura geométrica que se forma al
unir dos rayos(rectas) no coloniales, que se
comparten el mismo y único origen (vértice).
 La medida del Angulo alude a la medida
de su amplitud, es decir la medida de la
separación de sus lados.
m∢AOB: Medida del ∢AOB.
Entonces ; ∢AOB=β además
0°<β<180°

5. Son dos ángulos coplanares que
comparten un lado en común, además,
la intersección de las regiones interiores
determinadas por estos es nula.
Son aquellos ángulos tomados unos a
continuación de otro comparten un lado
en común y, a la intersección de las
regiones interiores determinadas por
estos, es nula además todos estos son
coplanares.

6. Son aquellos ángulos que comparten el
mismo vértice y sus lados de uno
representa rayos opuestos del otro.
Ojo: α= β

7.  ω=α (teorema de ángulos opuestos
por el vértice)
 θ= α (axioma de los ángulos
correspondientes)
 ω+α=θ+ω (sumando miembro a
miembro)finalmente: α=θ.
 β+α=180 (axioma del par lineal)
 α+180= α+θ +β (sumando miembro
a miembro) finalmente θ+β=180

8. Los teoremas son aquellos proposiciones que para ser verdaderas requieren
una demostración y se sujetan a los axiomas (postulados) teoremas
demostrados.

9. Ejemplo:
Calcular el valor de “x” en la
siguiente figura, aplique la ultima
propiedad.

10. En conclusión existe muchos tipos de ángulos
necesario conocer , ya que están presentes en
nuestra vida diaria, utilizamos sin darnos cuenta.

11. https://asesoriastlalpan.files.wordpress.com/2013/03/guia-de-
matemc3a1ticas.pdf
https://www.diigo.com/user/anccasivilla/b/393702090