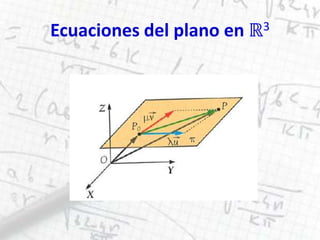
Este documento presenta los conceptos fundamentales de álgebra lineal y geometría del espacio, incluyendo espacios vectoriales, vectores, operaciones con vectores, sistemas de coordenadas, ecuaciones de rectas y planos en R3, y posiciones relativas entre rectas, planos y tres planos. Explica cada concepto con definiciones, ejemplos y aplicaciones.

1. ALGEBRA LINEALGEOMETRIA DEL ESPACIOPresentationby Miguel PerezFontenla, January 2011

2. ALGEBRA LINEALEspacios Vectoriales

3. Vectores. Operaciones

4. Geometría del Espacio

5. La Recta en el espacio

6. El plano en el espacio

7. Posiciones relativas …

8. Producto escalar

9. Perpendicularidad

10. Aplicaciones, distancias, ángulos …

11. Productos vectorial y mixto

12. Aplicaciones: Areas, distancias,

13. Aplicaciones: Volúmenes, distancias …Repasando ℝ2Vectores en el PlanoUn vector en ℝ2 queda determinado por dos puntos A(a1,a2) y B(b1,b2) (origen A y extremo B) y el orden de éstos:

14. Repasando ℝ2Operaciones con vectoresRepasando ℝ2

15. Definición: Espacio vectorialUn conjunto V con dos operaciones, una + y otra * y donde existen 0,1∊V y un cuerpo K (usualmente ℚ,ℝó ℂ) verificando:Respecto a +, Conmutativa AsociativaElemento neutroEl elemento simétrico de es su opuesto Respecto a *Distributiva respecto a la + de vectores Distributiva respecto a la + de escalares Asociativa mixta Elemento neutro Pues bien, a este conjunto formado por {V, +, *, K} que verifique todas las propiedades anteriores se le llama espacio vectorial sobre el cuerpo K

16. Otras definicionesDefinición: vectorA los elementos del espacio vectorial V se les llama vectoresLos denotaremos por letras Definición: escalarA los elementos del cuerpo (usualmente ℚ,ℝ ó ℂ)se les llama escalaresLos denotaremos con las letras griegas

17. Ejemplos de espacios vectorialesℝ2 plano euclídeo estudiado en Geometría plana

18. V2 o conjunto de vectores del plano, estudiado en Geometría plana

19. no conjunto de matricescuadradas n x n

20.  o conjunto de polinomios

21. V3 o conjunto de vectores libres del espacio

22. ℝ3 espacio euclídeoVectores en el espacioVectores en el espacioUn vector en ℝ3 queda determinado por dos puntos A y B (origen A y extremo B) y el orden de éstos.Elementos de un vectorVectores en el espacio

23. Operaciones con Vectores

24. Operaciones con Vectores

25. Combinación lineal de vectores

26. Combinación lineal de vectores

27. Base de un espacio vectorial

28. Base de un espacio vectorial

29. Coordenadas de un vectorSistemas de referenciaUn sistema de referencia en el espacio está formado por un punto fijo O y una base del espacio Lo denotaremos por El Sistema de referencia canónicoEs el que tiene como punto fijo O(0,0,0) el origeny como base tres vectores de módulo 1 y perpendiculares entre si

30. Coordenadas de un vectorCoordenadas y módulo de un vectorCoordenadas de un vectorEjercicio: Calcula las coordenadas y el módulo del vector

31. Coordenadas de un vectorEjercicio: Calcula las coordenadas y el módulo de estos vectores

32. Operaciones con coordenadasSuma y resta de vectores

33. Operaciones con coordenadasMultiplicación de un vector por un escalar

34. Operaciones con coordenadas

35. Operaciones con coordenadas

36. Operaciones con coordenadas

37. Operaciones con coordenadas

38. Aplicaciones de los vectoresPunto medio de un segmentoPuntos alineados

39. Aplicaciones de los vectores

40. El espacio euclídeoℝ3

41. Coordenadas de un vector en ℝ3

42. Sistemas de referencia en ℝ3Definimos sistema de referencia euclídeo del espacio (o también llamado sistema de referencia ortonormal) al conjunto formado por dondeO es un punto cualquiera fijo que denominamos origen de coordenadas

43. son los vectores de su base canónica de V3Ecuaciones de la recta en ℝ3Ecuación vectorialEcuación paramétricaEcuación continua Ecuación de la recta que pasa por dos puntosEcuación implícita o cartesiana

44. Ecuaciones de la recta en ℝ3Ecuación vectorial

45. Ecuaciones de la recta en ℝ3Ecuación paramétrica

46. Ecuaciones de la recta en ℝ3Ecuación continua

47. Ecuaciones de la recta en ℝ3Ecuación implícita (o cartesiana)

48. Ecuaciones de la recta en ℝ3EjemploCalcular todas las ecuaciones de la recta que pasa por A(3,1,2) y tiene un vector director

49. Ecuaciones de la recta en ℝ3Ejemplo. SoluciónCalcular todas las ecuaciones de la recta que pasa por A(3,1,2) y tiene un vector director Vectorial

50. Paramétrica

51. Continua

52. ImplícitaEcuaciones de la recta en ℝ3

53. Ecuaciones del plano en ℝ3Ecuación vectorialEcuación paramétricaEcuación General o implícita

54. Ecuaciones del plano en ℝ3

55. Ecuaciones del plano en ℝ3

56. Ecuaciones del plano en ℝ3

57. Ecuaciones del plano en ℝ3

58. Ecuaciones del plano en ℝ3

59. Ecuaciones del plano en ℝ3

60. Ecuaciones del plano en ℝ3Plano que pasa por 3 puntos

61. Ecuaciones del plano en ℝ3

62. Posiciones relativas 2 rectas en ℝ3¿Qué posiciones relativas se te ocurren?

63. Posiciones relativas 2 rectas en ℝ3ParalelasSecantesSe cruzanCoincidentes?

64. Posiciones relativas 2 rectas en ℝ3

65. Posiciones relativas 2 rectas en ℝ3

66. Posiciones relativas 2 rectas en ℝ3

67. Posiciones relativas 2 rectas en ℝ3

68. Posiciones relativas 2 rectas en ℝ3

69. Posiciones relativas 2 rectas en ℝ3Ejemplo

70. Posiciones relativas 2 rectas en ℝ3

71. Posiciones relativas 2 rectas en ℝ3

72. Posiciones relativas de recta y plano ¿Qué posiciones relativas se te ocurren?

73. Posiciones relativas de recta y plano en ℝ3Contenida

74. Secante

75. Paralela?

76. Posiciones relativas de recta y plano en ℝ3