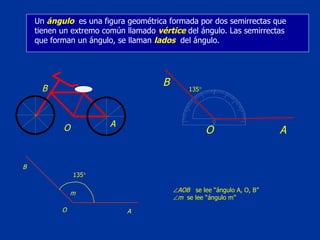
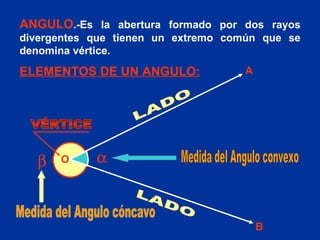
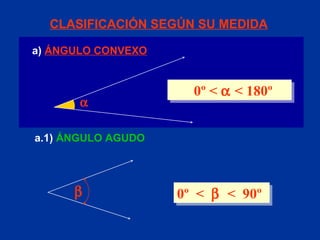
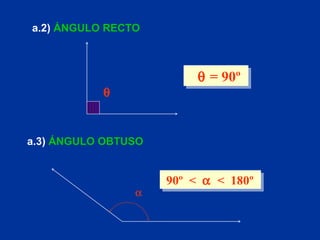
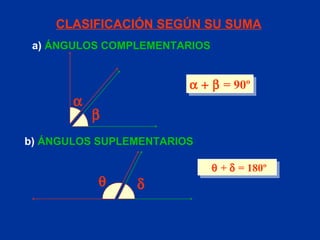
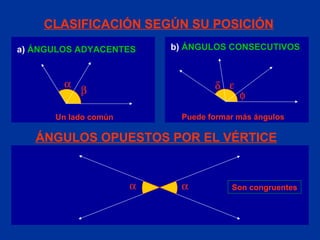
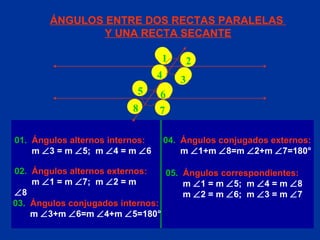
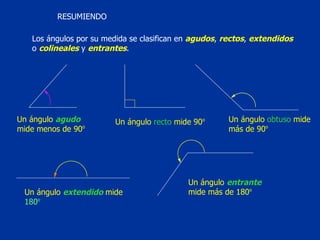
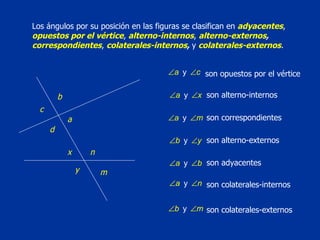
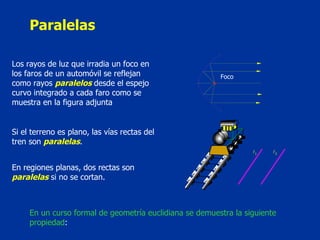
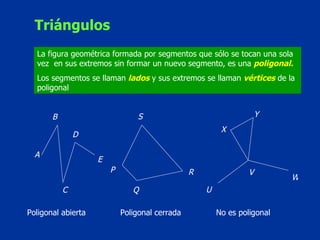
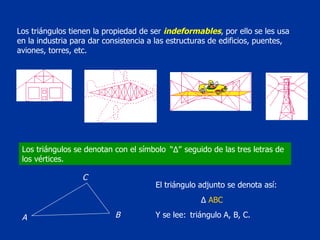
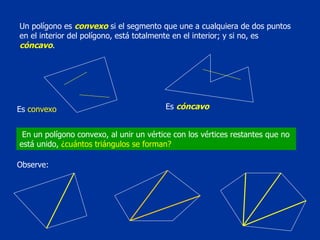
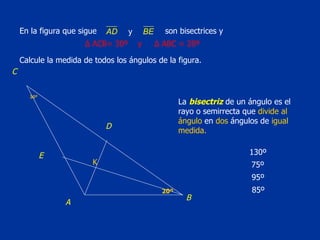
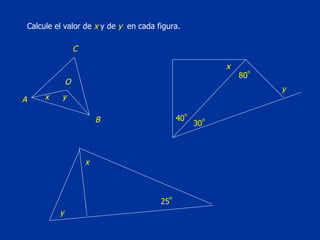
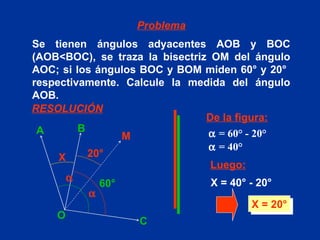
El documento explica conceptos básicos de geometría sobre ángulos. Define qué es un ángulo, sus elementos, y diferentes clasificaciones de ángulos según su medida, posición y relación con rectas paralelas. También introduce conceptos sobre triángulos como sus propiedades y clasificaciones.

1. GEOMETRÍA: ÁNGULOS

2. Conceptos básicos La huella que deja el lápiz al deslizarse pegado al borde de una regla es una línea recta . La huella que deja el lápiz estando fijo en la escritura, da idea de lo que es un punto . El geómetra griego Euclides (330 a. C. - 275 a.C.), decía: ¨Punto es lo que no tiene partes”. En realidad, Euclides se refería a punto como algo que no tiene largo ni ancho; o sea, una pequeña marca o señal sin dimensiones largo y ancho como la intersección de dos líneas. Los puntos se denotan con letras mayúsculas y las rectas con letras minúsculas cursivas, solas o con subíndices. ...   1 0 2 3 4 5 6 7 8    3  2 A B

3. Una línea recta tiene largo pero no tiene ancho. El largo de una línea recta no tiene fin; o sea, la línea recta es ilimitada. En los trazos se trabaja con partes de línea determinadas por dos puntos de ella, estas partes se llaman segmentos y a los puntos que los determinan se les llama extremos del segmento. A los segmentos se les denota con las letras de sus extremos colocándoles una raya encima. Por ejemplo, denota al segmento determinado por los puntos A y B , los cuales son extremos del segmento. La notación se lee “segmento A , B” . Cualquier punto de una línea recta, determina en ella, dos rayos o semirrectas ; en cuyo caso al punto se le llama extremo del rayo o de la semirrecta. A O B A A B C D O B O

4. Un ángulo es una figura geométrica formada por dos semirrectas que tienen un extremo común llamado vértice del ángulo. Las semirrectas que forman un ángulo, se llaman lados del ángulo. A O B m  AOB se lee “ángulo A, O, B”  m se lee “ángulo m” A 135  O B 135  A O B

5. ANGULO .-Es la abertura formado por dos rayos divergentes que tienen un extremo común que se denomina vértice. ELEMENTOS DE UN ANGULO:  LADO LADO VÉRTICE  Medida del Angulo convexo Medida del Angulo cóncavo O A B

6.  0º <  < 180º 0º <  < 90º CLASIFICACIÓN SEGÚN SU MEDIDA a) ÁNGULO CONVEXO a.1) ÁNGULO AGUDO 

7.  = 90º 90º <  < 180º a.2) ÁNGULO RECTO a.3) ÁNGULO OBTUSO  

8.    = 90º  +  = 180º CLASIFICACIÓN SEGÚN SU SUMA a) ÁNGULOS COMPLEMENTARIOS b) ÁNGULOS SUPLEMENTARIOS    

9. CLASIFICACIÓN SEGÚN SU POSICIÓN a) ÁNGULOS ADYACENTES b) ÁNGULOS CONSECUTIVOS ÁNGULOS OPUESTOS POR EL VÉRTICE Son congruentes Puede formar más ángulos Un lado común       

10. 01. Ángulos alternos internos: m  3 = m  5; m  4 = m  6 02. Ángulos alternos externos: m  1 = m  7; m  2 = m  8 03. Ángulos conjugados internos: m  3+m  6=m  4+m  5=180° 04. Ángulos conjugados externos: m  1+m  8=m  2+m  7=180° 05. Ángulos correspondientes: m  1 = m  5; m  4 = m  8 m  2 = m  6; m  3 = m  7 ÁNGULOS ENTRE DOS RECTAS PARALELAS Y UNA RECTA SECANTE 1 2 3 4 5 6 7 8

11. Los ángulos por su medida se clasifican en agudos , rectos , extendidos o colineales y entrantes . Un ángulo agudo mide menos de 90 o Un ángulo recto mide 90 o Un ángulo obtuso mide más de 90 o Un ángulo entrante mide más de 180 o Un ángulo extendido mide 180 o RESUMIENDO

12. Los ángulos por su posición en las figuras se clasifican en adyacentes , opuestos por el vértice , alterno-internos , alterno-externos , correspondientes , colaterales-internos , y colaterales-externos . a c b d y n x m son opuestos por el vértice son alterno-internos son correspondientes son alterno-externos son adyacentes son colaterales-internos son colaterales-externos

13. Los ángulos opuestos por el vértice son congruentes c b a Demostración: Porque forman un ángulo extendido ¿Por qué? ¿Por qué? ¿Por qué? < a + < c = 180º < b + < c = 180º < a + < c = < b + < c < a = < b

14. Paralelas Los rayos de luz que irradia un foco en los faros de un automóvil se reflejan como rayos paralelos desde el espejo curvo integrado a cada faro como se muestra en la figura adjunta Foco Si el terreno es plano, las vías rectas del tren son paralelas . En regiones planas, dos rectas son paralelas si no se cortan. En un curso formal de geometría euclidiana se demuestra la siguiente propiedad :  1  2

15. Los ángulos alterno-internos entre paralelas, tienen la misma medida. a b Si l 1 ∕∕ l 2 entonces < a = < b l 1 l 2

16. Triángulos La figura geométrica formada por segmentos que sólo se tocan una sola vez en sus extremos sin formar un nuevo segmento, es una poligonal. Los segmentos se llaman lados y sus extremos se llaman vértices de la poligonal A B S E D C R Q P Y X W V U Poligonal abierta Poligonal cerrada No es poligonal

17. Las poligonales cerradas se llaman polígonos . Los polígonos de tres lados se llaman triángulos . Los de cuatro se llaman cuadriláteros , los de cinco pentágonos , los de seis hexágonos , los de siete eptágonos , los de ocho octágonos , etc. Por costumbre, un polígono que tiene muchos lados se nombra indicando su número de lados, por ejemplo un polígono que tiene 9 lados, se nombra polígono de nueve lados . Y así sucesivamente. Un polígono es regular si sus lados son iguales entre sí; y si no, es irregular . Los triángulos se clasifican en: El isósceles tiene dos lados congruentes El equilátero tiene sus tres lados congruentes El escaleno no tiene lados congruentes

18. Los triángulos tienen la propiedad de ser indeformables , por ello se les usa en la industria para dar consistencia a las estructuras de edificios, puentes, aviones, torres, etc. Los triángulos se denotan con el símbolo seguido de las tres letras de los vértices. Y se lee: triángulo A, B, C. El triángulo adjunto se denota así: “ Δ ” Δ ABC A C B

19. En todo triángulo, la suma de sus ángulos interiores es igual a 180 o . a c b n m Trazo auxiliar: Para demostrar esta propiedad, por el vértice opuesto a la base del triángulo, trace una paralela a la base y observe que se forman los ángulo m y n respectivamente alterno-internos con los ángulos a y c en la base del triángulo. Demostración: Por construcción los ángulos a y m , y los ángulos c y n son alterno-internos entre paralelas, entonces: Pero los ángulos m , b y n forman un ángulo extendido, entonces: Sustituyendo a m y n por a y c respectivamente se tiene: Δ a + Δ b + Δ c = 180º Δ a = Δ m y Δ c = Δ n Δ m + Δ b + Δ n = 180º Δ a + Δ b + Δ c = 180º

20. Un polígono es convexo si el segmento que une a cualquiera de dos puntos en el interior del polígono, está totalmente en el interior; y si no, es cóncavo . Es convexo Es cóncavo En un polígono convexo, al unir un vértice con los vértices restantes que no está unido, ¿cuántos triángulos se forman? Observe:

21. En la figura que sigue son bisectrices y Calcule la medida de todos los ángulos de la figura. La bisectriz de un ángulo es el rayo o semirrecta que divide al ángulo en dos ángulos de igual medida. 30º 20º Δ ACB= 30º y Δ ABC = 20º 130º K 75º 95º 85º C E D B A

22. Calcule el valor de x y de y en cada figura. A B C O x y x y 25 o x y 40 o 80 o 30 o

23. Se tienen ángulos adyacentes AOB y BOC (AOB<BOC), se traza la bisectriz OM del ángulo AOC; si los ángulos BOC y BOM miden 60° y 20° respectivamente. Calcule la medida del ángulo AOB. De la figura:  = 60° - 20° Luego: X = 40° - 20°  = 40° X = 20° Problema RESOLUCIÓN A B O C M   60° 20° X

24. Fin