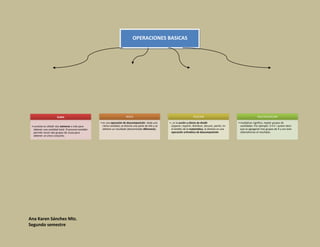
La suma y la resta son las operaciones matemáticas más básicas. La suma consiste en agregar cantidades para obtener un total, mientras que la resta es la operación inversa que implica eliminar una parte de una cantidad total. Otras operaciones como la multiplicación y la división también se describen brevemente, destacando que la división es la operación inversa a la multiplicación. Se explican algunas propiedades clave de cada operación.