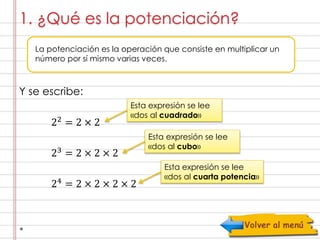
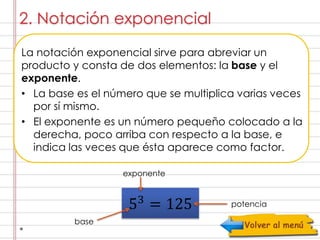
Este documento explica las potencias y sus propiedades. Define la potenciación como multiplicar un número por sí mismo varias veces y presenta la notación exponencial. Luego, detalla seis propiedades clave de las potencias: 1) cualquier número elevado a la potencia cero es igual a uno; 2) elevado a la potencia uno es igual a sí mismo; 3) el producto de potencias de la misma base es la suma de los exponentes; 4) dividir potencias de la misma base es restar los exponentes; 5) elevar una potencia a un exponente es multiplicar los exponent

1. Potenciación
CONTENIDOS
1. ¿Qué es la potenciación?
2. Notación exponencial
3. Propiedades de la potenciación
a) Potencia de exponente cero
b) Potencia de exponente uno
c) Producto de potencias de igual base
d) Cociente de potencias de igual base
e) Potencia de una potencia
f) Propiedad distributiva

2. 1. ¿Qué es la potenciación?
La potenciación es la operación que consiste en multiplicar un
número por sí mismo varias veces.
Y se escribe:
22 = 2 × 2
23 = 2 × 2 × 2
Esta expresión se lee
«dos al cuadrado»
24 = 2 × 2 × 2 × 2
Esta expresión se lee
«dos al cubo»
Esta expresión se lee
«dos al cuarta potencia»

3. 2. Notación exponencial
La notación exponencial sirve para abreviar un
producto y consta de dos elementos: la base y el
exponente.
• La base es el número que se multiplica varias veces
por sí mismo.
• El exponente es un número pequeño colocado a la
derecha, poco arriba con respecto a la base, e
indica las veces que ésta aparece como factor.
53 = 125
base
potencia
exponente

4. En general…
La potencia de base 푎 y exponente 푛 es el producto
de 푛 factores iguales al número 푎:
푎푛 = 푎 × 푎 × … × 푎
푛 factores
A la operación 푎푛 se le llama potenciación.

5. 3. Propiedades de la potenciación
Las propiedades de la potenciación son las que
permiten resolver por diferentes métodos una
potencia. Estas son:

6. a) Potencia de exponente cero
Para cualquier número 푎 elevado a la potencia 0 es
igual a la unidad. Observa:
Por ejemplo:
푎0 = 1
30 = 1 (−2)0= 1 푥0 = 1

7. b) Potencia de exponente uno
Cualquier número 푎 elevado a la potencia uno es
igual a la base. Observa:
Por ejemplo:
푎1 = 푎
71 = 7 (−5)1= −5 푦1 = 푦

8. c) Producto de potencias de igual base
Cuando dos potencias tienen la misma base, su
producto es igual a la misma base elevada a la
suma de los exponentes. Observa:
푎푚 ∙ 푎푛 = 푎푚+푛
donde 푎 es un número cualquiera, y 푚 y 푛 son
números enteros positivos.
Por ejemplo:
32 ∙ 34 = 36 푥7 ∙ 푥5 = 푥12 8 ∙ 83 = 84

9. d) Cociente de potencias de igual base
Para dividir potencias de la misma base 푎, de
exponentes 푚 y 푛, con 푚 > 푛, restamos los
exponentes. Observa:
donde 푎 es un número cualquiera diferente de 0,
y 푚 y 푛 son números enteros positivos.
Por ejemplo:
푎푚
푎푛 = 푎푚−푛
58
52 = 58−2 = 56 푦7
푦3 = 푦7−3 = 푦4

10. e) Potencia de una potencia
Para cualquier número 푎 y cualesquiera números
enteros positivos 푚 y 푛:
(푎푚)푛= 푎푚 × 푎푚 × 푎푚 × … × 푎푚 = 푎푚푛
푛 veces
Es decir, la potencia de una potencia se halla
multiplicando los exponentes.
Por ejemplo:
(53)2= 56 (푥5)4= 푥20

11. f) Propiedad distributiva
Si dos o más factores se elevan a un exponente,
este afecta por igual a cada factor. Observa:
Por ejemplo:
(푥 ∙ 푦)푛= (푥푛)(푦푛)
(3)(9) 3 = (3)3(9)3