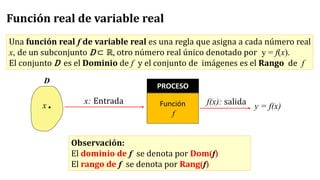
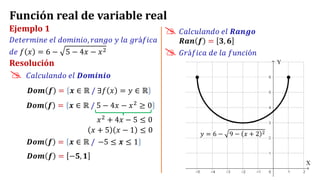
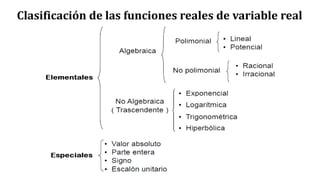
Este documento trata sobre funciones reales de variable real. Explica que una función real asigna a cada número real de un subconjunto del dominio otro número real único. Define dominio como el subconjunto de entrada y rango como el subconjunto de salida. Presenta ejemplos para ilustrar cómo calcular el dominio, rango y gráfica de funciones. También cubre clasificación de funciones, operaciones como adición y composición de funciones.

1. Facultad de Ingeniería Ambiental
Cálculo Diferencial
Semana 1. Funciones reales de variable real

2. Una función real f de variable real es una regla que asigna a cada número real
x, de un subconjunto D ⊂ ℝ, otro número real único denotado por y = f(x).
El conjunto D es el Dominio de f y el conjunto de imágenes es el Rango de f
x: Entrada Función
f
y = f(x)
f(x): salida
PROCESO
Observación:
El dominio de f se denota por Dom(f)
El rango de f se denota por Rang(f)
Función real de variable real
D
x .

3. Definiciones:
Función real de variable real:
DOMINIO
𝑫𝒐𝒎 𝒇 = 𝒙 ∈ ℝ / ∃𝑓 𝑥 = 𝑦 ∈ ℝ = 𝑫
RANGO o IMAGEN
𝑹𝒂𝒏 𝒇 = 𝒇 𝒙 = 𝒚 ∈ ℝ /. ∃ 𝑥 ∈ 𝐷𝑜𝑚𝑓
GRÁFICA
𝑮𝒓𝒂𝒇 𝒇 = (𝒙, 𝒚) ∈ ℝ2/ 𝑦 = 𝑓 𝑥 ; ∀𝑥 ∈ 𝐷
𝒇: ℝ → ℝ
𝒙 ↦ 𝒚 = 𝒇 𝒙
Gráficamente:
La gráfica de 𝒇 se interpreta geométricamente como una línea en el
espacio bidimensional, y se dice que 𝒚 = 𝒇 𝒙 es la ecuación en forma
explícita de la línea.
X
Y
Dom( f )
Ran( f )
Graf( f )
𝒙, 𝒚
𝒙
𝒇(𝒙)
𝑦 = 𝑓(𝑥)
𝒚 =

4. Ejemplo 1
Función real de variable real
𝐷𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑒 𝑒𝑙 𝑑𝑜𝑚𝑖𝑛𝑖𝑜, 𝑟𝑎𝑛𝑔𝑜 𝑦 𝑙𝑎 𝑔𝑟á𝑓𝑖𝑐𝑎
𝑑𝑒 𝑓 𝑥 = 6 − 5 − 4𝑥 − 𝑥2
𝐶𝑎𝑙𝑐𝑢𝑙𝑎𝑛𝑑𝑜 𝑒𝑙 𝑫𝒐𝒎𝒊𝒏𝒊𝒐

𝑫𝒐𝒎 𝒇 = 𝒙 ∈ ℝ /.5 − 4𝑥 − 𝑥2
≥ 0
𝑥2
+ 4𝑥 − 5 ≤ 0
𝑥 + 5 𝑥 − 1 ≤ 0
𝑫𝒐𝒎 𝒇 = 𝒙 ∈ ℝ /. −5 ≤ 𝒙 ≤ 1
Resolución
𝑫𝒐𝒎 𝒇 = 𝒙 ∈ ℝ / ∃𝑓 𝑥 = 𝑦 ∈ ℝ
𝑫𝒐𝒎 𝒇 = −𝟓, 𝟏
𝐶𝑎𝑙𝑐𝑢𝑙𝑎𝑛𝑑𝑜 𝑒𝑙 𝑹𝒂𝒏𝒈𝒐

𝑹𝒂𝒏 𝒇 = 𝒇 𝒙 = 𝒚 ∈ ℝ /. ∃ 𝑥 ∈ 𝐷𝑜𝑚𝑓
𝑆𝑖 𝑥 ∈ 𝐷𝑜𝑚𝑓 → −5 ≤ 𝑥 ≤ 1
𝐿𝑎 𝑟𝑒𝑔𝑙𝑎 𝑑𝑒 𝑐𝑜𝑟𝑟𝑒𝑠𝑝𝑜𝑛𝑑𝑒𝑛𝑐𝑖𝑎 𝑑𝑒 𝑓 𝑒𝑠
𝑒𝑞𝑢𝑖𝑣𝑎𝑙𝑒𝑛𝑡𝑒 𝑎 𝑦 = 6 − 9 − 𝑥 + 2 2
𝐿𝑢𝑒𝑔𝑜:
→ −3 ≤ 𝑥 + 2 ≤ 3
→ 0 ≤ 𝑥 + 2 ≤ 3
→ 0 ≤ 𝑥 + 2 2
≤ 9
→ 0 ≤ 9 − 𝑥 + 2 2
≤ 9
→ 3 ≤ 6 − 9 − 𝑥 + 2 2 ≤ 6
→ 3 ≤ 𝑦 ≤ 6
𝑹𝒂𝒏 𝒇 = 𝟑, 𝟔

5. Ejemplo 1
Función real de variable real
𝐷𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑒 𝑒𝑙 𝑑𝑜𝑚𝑖𝑛𝑖𝑜, 𝑟𝑎𝑛𝑔𝑜 𝑦 𝑙𝑎 𝑔𝑟á𝑓𝑖𝑐𝑎
𝑑𝑒 𝑓 𝑥 = 6 − 5 − 4𝑥 − 𝑥2
𝐶𝑎𝑙𝑐𝑢𝑙𝑎𝑛𝑑𝑜 𝑒𝑙 𝑫𝒐𝒎𝒊𝒏𝒊𝒐

𝑫𝒐𝒎 𝒇 = 𝒙 ∈ ℝ /.5 − 4𝑥 − 𝑥2
≥ 0
𝑥2
+ 4𝑥 − 5 ≤ 0
𝑥 + 5 𝑥 − 1 ≤ 0
𝑫𝒐𝒎 𝒇 = 𝒙 ∈ ℝ /. −5 ≤ 𝒙 ≤ 1
Resolución
𝑫𝒐𝒎 𝒇 = 𝒙 ∈ ℝ / ∃𝑓 𝑥 = 𝑦 ∈ ℝ
𝑫𝒐𝒎 𝒇 = −𝟓, 𝟏
𝐶𝑎𝑙𝑐𝑢𝑙𝑎𝑛𝑑𝑜 𝑒𝑙 𝑹𝒂𝒏𝒈𝒐

𝑹𝒂𝒏 𝒇 = 𝟑, 𝟔
𝐺𝑟á𝑓𝑖𝑐𝑎 𝑑𝑒 𝑙𝑎 𝑓𝑢𝑛𝑐𝑖ó𝑛

X
Y
𝑦 = 6 − 9 − 𝑥 + 2 2

6. Ejemplo 2
Si x representa la longitud del radio de una esfera, escribir
el valor de su DIÁMETRO, SUPERFICIE y VOLUMEN en
función de dicha longitud.
Resolución
 DIÁMETRO:
 SUPERFICIE:
 VOLUMEN:
❑ ¿Cuál es el dominio y rango
de las tres funciones?
❑ ¿Cuál es el dominio y rango de
dichos modelos matemáticos?
S
𝒙 = 𝟐𝒙
D
𝒙 =𝟒𝝅𝒙𝟐
V
𝒙 =
𝟒
𝟑
𝝅𝒙𝟑
Función real de variable real
x
D
S
V

7. Clasificación de las funciones reales de variable real

8. Algebra de Funciones
1) Igualdad de funciones.
2) Operaciones con funciones.
2.1. Adición de funciones.
2.2. Sustracción de funciones.
2.3. Multiplicación de funciones.
2.4. División de funciones.
Función real de variable real

9. 1. IGUALDAD DE FUNCIONES
a) 𝐷𝑓 = 𝐷𝑔
b) 𝑓 𝑥 = 𝑔 𝑥 , . ∀𝑥 ∈ 𝐷𝑓 = 𝐷𝑔
Ejemplo 1
Las funciones y son iguales, puesto que:
𝑓 𝑥 = 𝑥2
− 𝑥 𝑔 𝑥 = 𝑥(𝑥 − 1)
a) 𝐷𝑓 = ℝ = 𝐷𝑔
b) 𝑓 𝑥 = 𝑥2
− 𝑥 = 𝑥 𝑥 − 1 = 𝑔 𝑥 , ∀𝑥 ∈ ℝ
Ejemplo 2
Las funciones y no son iguales, pues no satisfacen la
𝑓 𝑥 =
𝑥2 − 1
𝑥 + 1
𝑔 𝑥 = 𝑥 − 1
primera condición: 𝐷𝑓 = ℝ − −1 ≠ ℝ = 𝐷𝑔
Sean las funciones y tal que .
𝑓: ℝ → ℝ 𝑔: ℝ → ℝ 𝐷𝑓 ∩ 𝐷𝑔 ≠ ∅ Decimos que y son
𝑓 𝑔
funciones iguales si y sólo si:

10. 2. OPERACIONES CON FUNCIONES
a) 𝐷𝑓+𝑔 = 𝐷𝑓 ∩ 𝐷𝑔
b) 𝑓 + 𝑔 𝑥 = 𝑓 𝑥 + 𝑔 𝑥 , . ∀𝑥 ∈ 𝐷𝑓 ∩ 𝐷𝑔
2.1 Adición de Funciones
Sean las funciones 𝑓 y 𝑔 con dominio 𝐷𝑓 y 𝐷𝑔 respectivamente, definimos la
adición de 𝑓 y 𝑔 como:
Ejemplo
a) Dominio: 𝐷𝑓+𝑔 = 𝐷𝑓 ∩ 𝐷𝑔 = ℝ ∩ ℝ = ℝ
b) Adición: 𝑓 + 𝑔 𝑥 = 𝑓 𝑥 + 𝑔 𝑥 = 7𝑥3 − 𝑥 − 1
Hallar , si y
𝑓 𝑥 = 5𝑥3 + 2𝑥 − 5 𝑔 𝑥 = 2𝑥3
− 3𝑥 + 4
𝑓 + g
Solución

11. 2. OPERACIONES CON FUNCIONES
a) 𝐷𝑓−𝑔 = 𝐷𝑓 ∩ 𝐷𝑔
b) 𝑓 − 𝑔 𝑥 = 𝑓 𝑥 − 𝑔 𝑥 , . ∀𝑥 ∈ 𝐷𝑓 ∩ 𝐷𝑔
2.2 Sustracción de Funciones
Sean las funciones 𝑓 y 𝑔 con dominio 𝐷𝑓 y 𝐷𝑔 respectivamente, definimos la
sustracción de 𝑓 y 𝑔 como:
Ejemplo
a) Dominio: 𝐷𝑓−𝑔 = 𝐷𝑓 ∩ 𝐷𝑔 = ℝ ∩ ℝ = ℝ
b) Sustracción: 𝑓 − 𝑔 𝑥 = 𝑓 𝑥 − 𝑔 𝑥 = 3𝑥3 + 5𝑥 − 9
Hallar , si y
𝑓 𝑥 = 5𝑥3 + 2𝑥 − 5 𝑔 𝑥 = 2𝑥3
− 3𝑥 + 4
𝑓 − g
Solución

12. 2. OPERACIONES CON FUNCIONES
a) 𝐷𝑓.𝑔 = 𝐷𝑓 ∩ 𝐷𝑔
b) 𝑓. 𝑔 𝑥 = 𝑓 𝑥 . 𝑔 𝑥 , . ∀𝑥 ∈ 𝐷𝑓 ∩ 𝐷𝑔
2.3 Multiplicación de Funciones
Sean las funciones 𝑓 y 𝑔 con dominio 𝐷𝑓 y 𝐷𝑔 respectivamente, definimos la
multiplicación de 𝑓 y 𝑔 como:
Ejemplo
a) Dominio: 𝐷𝑓.𝑔 = 𝐷𝑓 ∩ 𝐷𝑔 = ℝ ∩ ℝ = ℝ
b) Multiplicación: 𝑓. 𝑔 𝑥 = 𝑓 𝑥 . 𝑔 𝑥 = 6𝑥6 − 5𝑥4 − 7𝑥3 − 6𝑥2 + 17𝑥 − 5
Hallar , si y
𝑓 𝑥 = 5𝑥3 + 2𝑥 − 5 𝑔 𝑥 = 2𝑥3
− 3𝑥 + 4
𝑓. g
Solución

13. 2. OPERACIONES CON FUNCIONES
a) 𝐷𝑓/𝑔 = 𝐷𝑓 ∩ 𝐷𝑔 − 𝑔 𝑥 = 0
b)
𝑓
𝑔
𝑥 =
𝑓 𝑥
𝑔 𝑥
, . ∀𝑥 ∈ 𝐷𝑓/𝑔
2.4 División de Funciones
Sean las funciones 𝑓 y 𝑔 con dominio 𝐷𝑓 y 𝐷𝑔 respectivamente, definimos la
división de 𝑓 y 𝑔 como:
Ejemplo
a) Dominio: 𝐷𝑓/𝑔 = 𝐷𝑓 ∩ 𝐷𝑔 − 𝑔 𝑥 = 0 = ℝ ∩ ℝ − 2𝑥3
− 𝑥2
− 2𝑥 + 1 = 0
b) División:
𝑓
𝑔
𝑥 =
3𝑥3
+ 2𝑥 − 5
2𝑥3 − 𝑥2 − 2𝑥 + 1
=
𝑥 − 1 3𝑥2
+ 3𝑥 + 5
𝑥 − 1 𝑥 + 1 2𝑥 − 1
=
3𝑥2
+ 3𝑥 + 5
𝑥 + 1 2𝑥 − 1
Hallar , si y
𝑓 𝑥 = 3𝑥3
+ 2𝑥 − 5 𝑔 𝑥 = 2𝑥3
− 𝑥2
− 2𝑥 + 1
𝑓/g
Solución
𝐷𝑓/𝑔 = ℝ − −1;
1
2
; 1

14. Composición de Funciones
1) Definición de Composición de funciones.
2) Propiedades.
3) Ejercicios.
Función real de variable real

15. Representación de funciones como máquinas
Considere las dos máquinas:
Si queremos obtener:
Horas Dinero ganado Dinero ganado Impuesto a pagar
Horas Impuesto a pagar ¿Qué deberíamos hacer?
Deberíamos ordenar secuencialmente las máquinas 𝑓 y 𝑔, es decir:
Impuesto a pagar
Horas Dinero ganado
y

16. x
g
f
Domg
Domf
Rang Ranf
f(g(x))
g(x)
f o g
𝐷𝑜𝑚𝑓𝑜g = 𝑥/𝑥 ∈ 𝐷𝑜𝑚g ∧ g(𝑥) ∈ 𝐷𝑜𝑚𝑓
1. DEFINICIÓN DE COMPOSICIÓN DE FUNCIONES
Si 𝒇 y 𝐠 son dos
funciones, entonces
g compuesta con 𝒇,
denotada por 𝒇𝒐𝐠 es
la función definida
por:
(𝑓𝑜g) 𝑥 = 𝑓(g 𝑥 )
donde el dominio de
𝒇𝒐𝐠 es el conjunto
de todas las 𝒙 en el
dominio de 𝐠 , tales
que 𝐠 𝒙 está en el
dominio de 𝒇.

17. Observación
Componer 𝑓 𝑐𝑜𝑛 𝑔 consiste sólo en acoplar la máquina 𝑔 con la de 𝑓; es decir le
suministramos a 𝑓, la producción de 𝑔.
Considerando a las funciones como máquinas, podemos entender la operación de
composición como un acoplamiento de una máquina con otra.
Por ejemplo, si tenemos la función 𝑓 𝑥 = 𝑥2
, la cual es una máquina que recibe 𝑥 y la
eleva al cuadrado; y otra función 𝑔 𝑥 = 2𝑥 + 3 que es una máquina que recibe 𝑥, lo
multiplica por 2 y luego le suma 3; entonces:
𝟐
y

18. Sean las funciones , y ; entonces tenemos las siguientes propiedades:
𝑓 𝑔 ℎ
P1)
𝑓 𝑜 𝑔 ≠ 𝑔 𝑜 𝑓
La composición de funciones es no conmutativa, es decir:
P2)
(𝑓 𝑜 𝑔) 𝑜 ℎ = 𝑓 𝑜 (𝑔 𝑜 ℎ)
La composición de funciones es asociativa, es decir:
P3) (𝑓 + 𝑔) 𝑜 ℎ = 𝑓 𝑜 ℎ + (𝑔 𝑜 ℎ)
P4) (𝑓. 𝑔) 𝑜 ℎ = 𝑓 𝑜 ℎ . (𝑔 𝑜 ℎ)
Si es la función identidad, luego:
I
P5) 𝑓 𝑜 I = 𝑓 y I 𝑜 𝑓 = 𝑓
P6) I𝑛 𝑜 𝑓 = 𝑓𝑛, ∀𝑛 ∈ ℤ+
2. PROPIEDADES

19. 3. EJEMPLOS
Dadas las funciones: F={(1;2),(2;3),(3;1),(4;1),(5;0)} y G={(0;2),(1;3),(2;0),(3;4),(4;6)}.
Calcular, si existe: F o G
3.1
Solución:
Una manera práctica de hallar F o G es mediante diagramas, en donde cada par
ordenado se traduce en una flecha. Primero graficamos G y enseguida graficamos F.
Considerando los elementos asociados a las flechas que hacen el recorrido completo,
tenemos:
0
1
2
3
4
2
3
0
4
6
1
5
0
1
2
3
G F
F o G
F o G = {(0;3),(1;1),(3;1)}

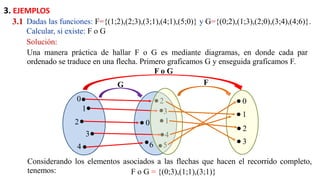
20. Solución:
Dadas las funciones: y
3.2 𝑓 𝑥 = 4𝑥 − 𝑥2 𝑔 𝑥 = 𝑥 − 2. Hallar, si existe, 𝑓 o g
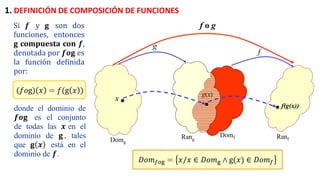
Hallamos 𝐷𝑜𝑚𝑓𝑜𝑔
✓
Por definición: 𝐷𝑜𝑚𝑓𝑜𝑔 = 𝑥/𝑥 ∈ 𝐷𝑜𝑚𝑔 ∧ 𝑔(𝑥) ∈ 𝐷𝑜𝑚𝑓
𝑥 ∈ ℝ (𝑥 − 2) ∈ [0,4]
𝑥 ∈ [2,6]
∧
𝐷𝑜𝑚𝑓𝑜𝑔 =
Hallamos 𝑓 𝑜 𝑔
✓
Por definición: 𝑓 𝑜 𝑔 𝑥 = 𝑓 𝑔 𝑥 = 𝑓(𝑥 − 2)
𝑓 𝑜 𝑔 𝑥 = 4 𝑥 − 2 − (𝑥 − 2)2
𝑓 𝑜 𝑔 𝑥 = −𝑥2 + 8𝑥 − 12 𝑐𝑜𝑛 𝑥 ∈ [2,6]
3. EJEMPLOS

21. Función Máximo Entero
𝑓: D ⊂ ℝ → ℝ / 𝑓 𝑥 = 𝑥
Dominio:
Rango :
𝑥 ∈ ℝ

 𝑦 ∈ ℤ
 Gráfica :
Para realizar la gráfica
aplicamos el teorema:
∀ 𝑥 ∈ ℝ con 𝑛 ∈ ℤ ∶
𝑥 = 𝑛 ↔ 𝑛 ≤ 𝑥 < 𝑛 + 1
Veamos:
Si −𝟑 ≤ 𝑥 < −2 entonces 𝑓 𝑥 = −𝟑
Si −𝟐 ≤ 𝑥 < −1 entonces 𝑓 𝑥 = −𝟐
𝑦 = 𝑥
…
𝑦 = 𝑥

22. 𝑥 − 𝑥 ≥ 0
↔
Ejemplo 1
Determinar el dominio y luego graficar: 𝑓 𝑥 =
𝑥 𝑥 − 𝑥
1 − 𝑥 − 𝑥 1 + 𝑥 − 𝑥
Resolución
 Calculando el dominio.
De las raíces cuadradas tenemos:
∧ 𝑥 − 𝑥 ≥ 0
𝑥 ≤ 𝑥 ∧ 𝑥 ≥ 𝑥
𝑥 = 𝑥 𝑥 ∈ ℤ
Como 𝑥 ∈ ℤ entonces:
1 − 𝑥 − 𝑥 ≠ 0
lo cual garantiza la existencia de
la función.
 Graficando.
Considerando el dominio, la regla
de correspondencia se reduce a:
𝑓 𝑥 = 𝑥 𝑥 − 𝑥
Luego:
Si 𝑥 ∈ ℤ−
entonces 𝑓 𝑥 = −2𝑥2
Si entonces 𝑓 𝑥 = 0
𝑥 ∈ ℤ+
0
Por lo tanto:
𝑓 𝑥 = ቊ
−2𝑥2 , 𝑥 ∈ ℤ−
0 , 𝑥 ∈ ℤ+
0

23. Ejemplo 1
Graficando: 𝑓 𝑥 = ቊ
−2𝑥2
, 𝑥 ∈ ℤ−
0 , 𝑥 ∈ ℤ+
0
Si 𝑥 = −2 entonces 𝑦 = −8
𝑥 = −1 entonces 𝑦 = −2
Si
𝑥 =0 entonces 𝑦 = 0
Si

24. Ejemplo 2
Resolución
Hallando el dominio y regla de
correspondencia de 𝑓𝑜𝑓.
Sea
Considerando 𝑓 𝑥 = ቊ
1/𝑥 , . . 𝑥 < 0
−𝑥2 , . . 𝑥 > 0
y
g 𝑥 =
𝑥2
1 + 2𝑥
, . 𝑥 < 1 graficar 𝑓𝑜𝑓 . g
𝑓1 𝑥 = 1/𝑥 , . 𝑥 < 0 y
𝑓2 𝑥 = −𝑥2
, . 𝑥 > 0 entonces:
∎ 𝐷𝑜𝑚 𝑓1𝑜𝑓1 𝑥 ∈ ℝ /𝑥 < 0 ∧ 1/𝑥 < 0
= 𝑥 ∈ ℝ / 𝑥 < 0
𝑓1𝑜𝑓1 (𝑥) =𝑓1 𝑓1(𝑥) =𝑓1 1/𝑥 = 𝑥
𝑓1𝑜𝑓1 𝑥 = 𝑥 , . 𝑥 < 0
∎ 𝐷𝑜𝑚 𝑓1𝑜𝑓2 𝑥 ∈ ℝ /𝑥 > 0 ∧ −𝑥2 < 0
=
=
= 𝑥 ∈ ℝ / 𝑥 > 0
𝑓1𝑜𝑓2 (𝑥) 𝑓1 𝑓2(𝑥) =𝑓1 −𝑥2 =−
1
𝑥2
=
𝑓1𝑜𝑓2 𝑥 = −
1
𝑥2
, . 𝑥 > 0
∎ 𝐷𝑜𝑚 𝑓2𝑜𝑓1 𝑥 ∈ ℝ /𝑥 < 0 ∧ 1/𝑥 > 0
=
= 𝑥 ∈ ∅
∎ 𝐷𝑜𝑚 𝑓2𝑜𝑓2 𝑥 ∈ ℝ /𝑥 > 0 ∧ −𝑥2 > 0
=
= 𝑥 ∈ ∅
Por lo tanto:
𝑓𝑜𝑓 𝑥 = ቐ
𝑥 , . . 𝑥 < 0
−
1
𝑥2
, . . 𝑥 > 0

25. Ejemplo 2
Resolución
Hallando una expresión equivalente para
el dominio y regla de correspondenciade g
Por propiedades, tenemos que:
Considerando 𝑓 𝑥 = ቊ
1/𝑥 , . . 𝑥 < 0
−𝑥2 , . . 𝑥 > 0
y g 𝑥 =
𝑥2
1 + 2𝑥 , . 𝑥 < 1 graficar 𝑓𝑜𝑓 . g
1 + 2𝑥 = 1 + 2𝑥
𝑥 < 1 ↔ −1 < 𝑥 < 1
entonces:
∎
→
1
2
< 2𝑥
< 1
Por lo tanto:
g 𝑥 = ൞
𝑥2, . . −1 < 𝑥 < 0
𝑥2
2
, . . 0 ≤ 𝑥 < 1
g 𝑥 =
𝑥2
1 + 2𝑥 , . −1 < 𝑥 < 1
✓
✓
Ahora, considerando el máximo entero
particionamos el dominio en la forma:
−1 < 𝑥 < 1 ≡ −1 < 𝑥 < 0 ∨ 0 ≤ 𝑥 < 1
Luego:
𝑆𝑖 −1 < 𝑥 < 0 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠
2𝑥
= 0 g 𝑥 = 𝑥2
, . −1 < 𝑥 < 0
∎
→
1 ≤ 2𝑥
< 2
𝑆𝑖 0 ≤ 𝑥 < 1 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠
2𝑥 = 1 g 𝑥 =
𝑥2
2
, .0 ≤ 𝑥 < 1

26. Ejemplo 2
Resolución
Graficando 𝑓𝑜𝑓 . g
Como:
Considerando 𝑓 𝑥 = ቊ
1/𝑥 , . . 𝑥 < 0
−𝑥2 , . . 𝑥 > 0
y g 𝑥 =
𝑥2
1 + 2𝑥 , . 𝑥 < 1 graficar 𝑓𝑜𝑓 . g
y
entonces:
𝑓𝑜𝑓 𝑥 = ቐ
𝑥 , . . 𝑥 < 0
−
1
𝑥2 , . . 𝑥 > 0
g 𝑥 = ൞
𝑥2, . . −1 < 𝑥 < 0
𝑥2
2
, . . 0 ≤ 𝑥 < 1
𝑓𝑜𝑓 . g 𝑥 = ൞
𝑥3
, . . −1 < 𝑥 < 0
−
1
2
, . . 0 < 𝑥 < 1

27. Y
X
Función Signo
𝑓: ℝ → ℝ / 𝑓 𝑥 = sgn(𝑥)
Dominio:
Rango :
𝑥 ∈ ℝ

 𝑦 ∈ −1,0,1
 Gráfica :
sgn(𝑥) = ቐ
−1 , 𝑠𝑖 𝑥 < 0
0 , 𝑠𝑖 𝑥 = 0
1 , 𝑠𝑖 𝑥 > 0
𝐷𝑜𝑛𝑑𝑒 𝑒𝑙 𝑠𝑖𝑔𝑛𝑜 𝑑𝑒 𝑥 𝑑𝑒𝑛𝑜𝑡𝑎𝑑𝑜
𝑝𝑜𝑟 sgn 𝑥 𝑠𝑒 𝑑𝑒𝑓𝑖𝑛𝑒 𝑐𝑜𝑚𝑜:

28. Y
X
Función Escalón Unitario
𝑓: ℝ → ℝ / 𝑓 𝑥 = 𝑢 𝑥 = ቊ
0 , 𝑠𝑖 𝑥 < 0
1 , 𝑠𝑖 𝑥 ≥ 0
Dominio:
Rango :
𝑥 ∈ ℝ

 𝑦 ∈ 0 ; 1
 Gráfica :
Función de Heaviside
En el análisis matemático de circuitos o señales, resulta conveniente
definir una función especial que es 0 (apagado) hasta cierto número y
luego es 1 (encendido) después de lo anterior.
La función de Heaviside recibe su nombre
en honor al brillante ingeniero electrónico y matemático inglés Oliver
Heaviside (1850-1925)
𝑈 𝑥 − 𝑎 = ቊ
0 , 𝑠𝑖 𝑥 < 𝑎
1 , 𝑠𝑖 𝑥 ≥ 𝑎

29. Función Escalón Unitario
𝑓 𝑥 =
𝑓1 ,
𝑓2 ,
𝑓3 ,
𝑥 < 𝑎1
𝑎1 ≤ 𝑥 < 𝑎2
𝑎2 ≤ 𝑥 < 𝑎3
⋮
𝑓𝑛−1 ,
𝑓𝑛 ,
⋮
𝑎𝑛−2 ≤ 𝑥 < 𝑎𝑛−1
𝑎𝑛−1 ≤ 𝑥
𝑓 𝑥 = 𝑓1 + 𝑓2 − 𝑓1 . 𝑢 𝑥 − 𝑎1 + 𝑓3 − 𝑓2 . 𝑢 𝑥 − 𝑎2 + ⋯ + 𝑓𝑛 − 𝑓𝑛−1 . 𝑢 𝑥 − 𝑎𝑛−1
𝑻𝑬𝑶𝑹𝑬𝑴𝑨.
D𝑎𝑑𝑎 𝑙𝑎 𝑓𝑢𝑛𝑐𝑖ó𝑛 𝑠𝑒𝑐𝑐𝑖𝑜𝑛𝑎𝑑𝑎 𝑠𝑒 𝑐𝑢𝑚𝑝𝑙𝑒 𝑞𝑢𝑒:
𝐸𝑗𝑒𝑚𝑝𝑙𝑜.
Si 𝑓 𝑥 =
𝑥 , 𝑥 < −2
−𝑥2
, −2 ≤ 𝑥 < 0
𝑠𝑒𝑛𝑥 , 0 ≤ 𝑥 < 𝜋
𝑙𝑛𝑥 , 𝑥 ≥ 𝜋
entonces aplicando el teorema tenemos que:
𝑓 𝑥 = 𝑥 + −𝑥2 − 𝑥 . 𝑢 𝑥 + 2 + 𝑠𝑒𝑛𝑥 + 𝑥2 . 𝑢 𝑥 − 0 + 𝑙𝑛𝑥 − 𝑠𝑒𝑛𝑥 . 𝑢 𝑥 − 𝜋

30. Funciones Hiperbólicas
Seno Hiperbólico Coseno Hiperbólico Tangente Hiperbólico
𝑠𝑒𝑛ℎ(𝑥) =
𝑒𝑥 − 𝑒−𝑥
2
cosh(𝑥) =
𝑒𝑥 + 𝑒−𝑥
2
tanh(𝑥) =
𝑒𝑥 − 𝑒−𝑥
𝑒𝑥 + 𝑒−𝑥
𝑓(𝑥) = 𝑠𝑒𝑛ℎ(𝑥)
𝑦 =
𝑒𝑥
2
𝑦 = −
𝑒−𝑥
2
𝑓(𝑥) = 𝑐𝑜𝑠ℎ(𝑥)
𝑦 =
𝑒𝑥
2
𝑦 =
𝑒−𝑥
2
𝑓(𝑥) = 𝑡𝑎𝑛ℎ(𝑥)
𝑦 = 1
𝑦 = −1

31. Funciones Hiperbólicas
Cotangente Hiperbólico Secante Hiperbólico Cosecante Hiperbólico
𝑐𝑜𝑡ℎ(𝑥) =
𝑒𝑥 + 𝑒−𝑥
𝑒𝑥 − 𝑒−𝑥
sech(𝑥) =
2
𝑒𝑥 + 𝑒−𝑥 csch(𝑥) =
2
𝑒𝑥 − 𝑒−𝑥
𝑓(𝑥) = 𝑐𝑜𝑡ℎ(𝑥)
𝑦 = 1
𝑦 = −1
𝑓(𝑥) = 𝑠𝑒𝑐ℎ(𝑥)
𝑓(𝑥) = 𝑐𝑠𝑐ℎ(𝑥)

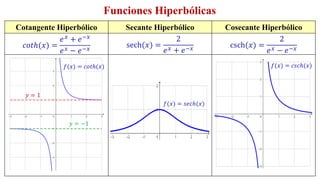
32. Función Regla Dominio Rango Asíntotas
Seno hiperbólico 𝑠𝑒𝑛ℎ𝑥 =
𝑒𝑥
− 𝑒−𝑥
2
ℝ ℝ 𝑦 = ±
𝑒±𝑥
2
Coseno hiperbólico 𝑐𝑜𝑠ℎ𝑥 =
𝑒𝑥 + 𝑒−𝑥
2
ℝ [1, + ۧ
∞ 𝑦 =
𝑒±𝑥
2
Tangente hiperbólica 𝑡𝑎𝑛ℎ𝑥 =
𝑒𝑥
− 𝑒−𝑥
𝑒𝑥 + 𝑒−𝑥
ℝ −1, 1 𝑦 = ±1
Cotangente hiperbólica 𝑐𝑜𝑡ℎ𝑥 =
𝑒𝑥 + 𝑒−𝑥
𝑒𝑥 − 𝑒−𝑥
ℝ − 0 −∞, −1 ∪ 1, +∞ 𝑦 = ±1
Secante hiperbólica 𝑠𝑒𝑐ℎ𝑥 =
2
𝑒𝑥 + 𝑒−𝑥
ℝ ‫ۦ‬0, ]
1 𝑦 = 0
Cosecante hiperbólica 𝑐𝑠𝑐ℎ𝑥 =
2
𝑒𝑥 − 𝑒−𝑥
ℝ − 0 ℝ − 0 𝑥 = 0