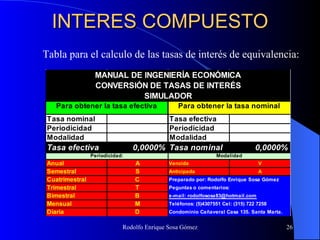
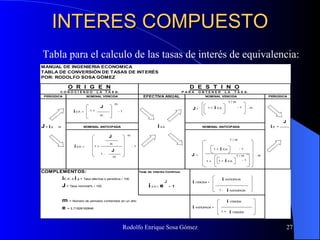
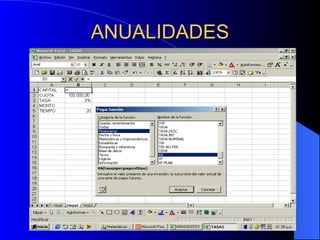
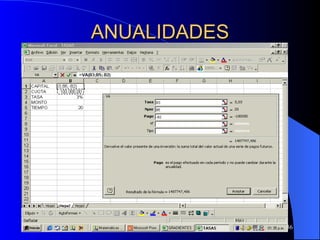
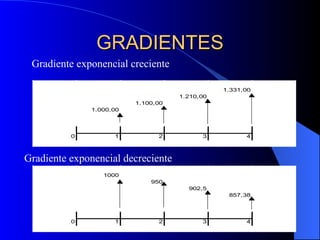
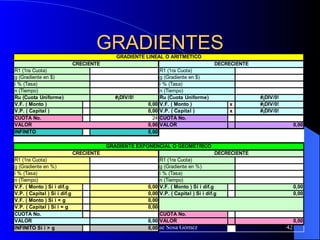
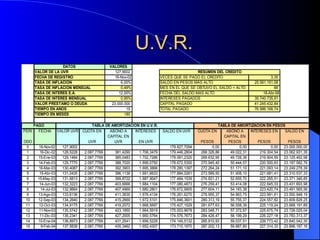
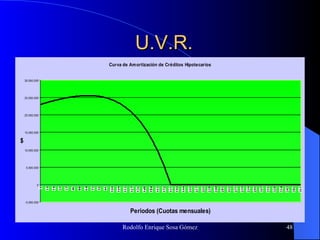
Este documento trata sobre conceptos básicos de matemáticas financieras. Explica variables como capital, tiempo, tasa de interés e interés y diferentes tipos de interés como simple y compuesto. También cubre temas como valor futuro, valor presente, anualidades, gradientes y evaluaciones financieras como flujo de caja y VPN. Finalmente, introduce el concepto de Unidad de Valor Real (UVR) y cómo calcularla.

1. MATEMATICAS FINANCIERAS TECNICAS FINANCIERAS CUANTITATIVAS

2. MATEMATICAS FINANCIERAS Las Matemáticas Financieras o Ingeniería Económica tienen como objetivo fundamental el estudio y análisis de todas aquellas operaciones y planteamientos en los cuales intervienen las magnitudes de: Capital, Interés, Tiempo y Tasa.

3. MATEMATICAS FINANCIERAS La Matemática Financiera la podemos asociar con dos símbolos es decir el de los números (#) y el de los pesos ($), ya, que cuando hablamos de Matemáticas automáticamente hacemos relación con los números; y cuando hablamos de Finanzas lo relacionamos con el signo pesos; de allí la asociación.

4. MATEMATICAS FINANCIERAS Variables financieras: Capital C Tiempo t Tasa i Interés I Cuota R Monto M

5. VALOR DEL DINERO EN EL TIEMPO NUNCA SE DEBEN SUMAR VALORES EN FECHAS DIFERENTES

6. INTERES ES LO QUE SE PAGA O SE RECIBE POR CIERTA CANTIDAD DE DINERO TOMADA O DADA EN PRESTAMO

7. INTERES SIMPLE Es aquel interes que se genera sobre un capital que permanece constante en el tiempo.

8. INTERES SIMPLE Formula general de la tasa de interés: i = I / C Si condicionamos esta formula a la expresión de unidades de tiempo se obtiene la siguiente ecuación: I = i . C . t

9. INTERES SIMPLE Clasificación del interés simple: Interés simple comercial en forma ordinaria Interés simple comercial en forma exacta Interés simple exacto en forma comercial Interes simple exacto en forma ordinaria

10. INTERES SIMPLE Clasificación del interés simple Interés simple comercial: 360 días al año, 180 días al semestre, 90 días al trimestre, 30 días al mes Interés simple exacto: 365 días al año Tabla o calculadora para las demás equivalencias

11. INTERES SIMPLE Valor futuro a interés simple: Tambien conocido como monto. Se deduce de la suma entre el capital y los intereses que se generan durante determinado período de tiempo M = C + I M = C + ( i . C . t ), luego por factorización M = C ( 1 + i . t )

12. INTERES SIMPLE Conceptode Equivalencia Financiera: Es la relación de igualdad que se establece entre una o unas deudas y uno o unos pagos en un momento determinado en el tiempo denominado fecha focal (momento de la negociación)

13. INTERES SIMPLE Equidad entre el tiempo y la tasa: - La tasa y el tiempo siempre deben ir expresadas en la misma unidad de base. - La tasa es la que condiciona la expresión del tiempo.

14. INTERES SIMPLE Series uniformes a interés simple: Series vencidas: Valor presente Valor futuro Series anticipadas Valor presente Valor futuro

15. INTERES COMPUESTO Concepto: Es el interés que se genera sobre intereses. Los intereses que se generan en el primer período de capitalización se convierten en capirtal para generar mas intereses para el segundo periódo de capitalización y así sucesivamente.

16. INTERES COMPUESTO Comparativo entre el interés simple y el interés compuesto

17. INTERES COMPUESTO Comparativo entre el interés simple y el interés compuesto

18. INTERES COMPUESTO FORMULA GENERAL

19. INTERES COMPUESTO Capital o valor presente: VA Tasa: TASA Monto o valor futuro: VF Tiempo: NPER Cuota: PAGO EXCEL

20. INTERES COMPUESTO

21. INTERES COMPUESTO

22. INTERES COMPUESTO

23. INTERES COMPUESTO Regla comercial:

24. INTERES COMPUESTO Regla de saldos insolutos:

25. INTERES COMPUESTO TASAS: TASA NOMIAL TASA EFECTIVA TASAS EQUIVALENTES TASAS ANTICIPADAS TASAS VENCIDAS

26. INTERES COMPUESTO Tabla para el calculo de las tasas de interés de equivalencia:

27. INTERES COMPUESTO Tabla para el calculo de las tasas de interés de equivalencia:

28. INTERES COMPUESTO FORMULAS

29. INTERES COMPUESTO FORMULAS

30. INTERES COMPUESTO INFLACION - I.P.C. DEVALUACION TASAS COMBINADAS TASAS DEFLACTADAS D.T.F. T.C.C. T.B.S. LIBOR PRIME RATE TMAR = T.I.O + Spreads

31. ANUALIDADES VENCIDAS ANTICIPADAS PERPETUAS DIFERIDAS PERPETUAS DIFERIDAS

32. ANUALIDADES

33. ANUALIDADES

34. ANUALIDADES

35. ANUALIDADES

36. ANUALIDADES

37. ANUALIDADES

38. GRADIENTES LINEALES O ARITMETICAS: CRECIENTES Y DECRECIENTES VALOR PRESENTE Y VALOR FUTURO CALCULO DE CUOTA GRADIENTE DIFERIDA GRADIENTE PERPETUA GRADIENTE PERPETUA DIFERIDA

39. GRADIENTES EXPONENCIALES O GEOMETRICAS CRECIENTES Y DECRECIENTES VALOR PRESENTE Y VALOR FUTURO CALCULO DE CUOTA GRADIENTE DIFERIDA GRADIENTE PERPETUA GRADIENTE PERPETUA DIFERIDA

40. GRADIENTES Gradiente lineal creciente Gradiente lineal decreciente

41. GRADIENTES Gradiente exponencial creciente Gradiente exponencial decreciente

42. GRADIENTES

43. EVALUACIONES FINANCIERAS FLUJO DE CAJA FLUJO DE CAJA NETO V.P.N. T.I.R.

44. U.V.R.

45. U.V.R. Procedimiento para el calculo de la U.V.R.

46. U.V.R. - UVR t = Valor de la moneda legal colombiana de la UVR Del día t del período de calculo. UVR 15 = Valor de la moneda legal colombiana de la UVR el día 15 de cada mes. i = Variación mensual del IPC durante el mes calendario inmediatamente anterior al mes de inicio del período de calculo t = Número de días calendario transcurridos desde el inicio de un período de calculo hasta el día de calculo de la UVR. Por lo tanto, t tendrá valores entre 1 y 31 de acuerdo con el número de días calendario del respectivo período de calculo. - d = Número de días calendario del respectivo período de calculo

47. U.V.R.

48. U.V.R.

49. MATEMATICAS FINANCIERAS TECNICAS FINANCIERAS CUANTITATIVAS FIN DE LA PRESENTACION RODOLFO SOSA GOMEZ