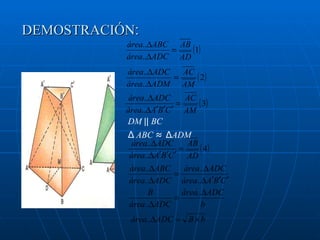
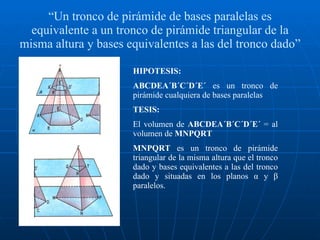
El documento trata sobre las pirámides y sus propiedades geométricas. Define una pirámide, sus elementos y clasificaciones. Explica fórmulas para calcular la apotema, área lateral, área total y volumen de una pirámide regular. Presenta teoremas sobre pirámides con bases equivalentes y la descomposición de un tronco de pirámide.

1. INSTITUTO TECNOLÓGICO SUPERIOR “ DANIEL ÁLVAREZ BURNEO” GEOMETRÍA DEL ESPACIO DR. VICENTE MATAMOROS

2. Sitúa sobre los círculos de la serpiente los números del 1 al 9, de manera que cada línea de tres números, sume 13.

3. Sitúa sobre los círculos de la serpiente los números del 1 al 9, de manera que cada línea de tres números, sume 13.

5. PIRAMIDES

9. DEFINICIÓN Poliedro que tiene una cara llamada base, que es un polígono cualquiera y las otras, llamadas caras laterales, son triángulos que tienen un vértice común, llamado vértice o cúspide de la pirámide.

10. ELEMENTOS

11. CLASIFICACIÓN

12. Calculo de la apotema

13. Calculo de la arista

14. Cálculo de la apotema lateral b=15m a= 1,8m c=?

15. TEOREMAS

16. Área de una pirámide

17. Área lateral “ El área lateral de una pirámide regular es la mitad del producto del perímetro de la case y la apotema de la pirámide” Hipótesis: S-ABCDE pirámide regular Demostración: A ﺎ = área ∆ ASB . N área ∆ ASB = ½ AB . a A ﺎ = ½ AB . a n AB . n = p A ﺎ = ½ p a Tesis: A ﺎ = ½ p a S A B C D E S a

18. Área total El área total de una pirámide regular es la suma del área lateral y el área de la base A t = A ﺎ + A b A ﺎ = ½ p a A b = ½ p a’ A t = ½ p a + ½ p a’ A t = ½ p (a + a’)

19. Volumen de una pirámide

20. “ Si dos pirámides tienen bases equivalentes a la misma altura, entonces tienen el mismo volumen” Hipótesis: h altura de las pirámides V-ACD y O-PQRS B misma área de las bases Tesis: Pirámides V-ACD y O-PQRS tienen el mismo volumen Demostración: A’C’D’ y P’Q’R’S’ secciones transversales a las dos pirámides Sección A’C’D’ es equivalente a P’Q’R’S’ Pirámides V-ACD y O-PQRS tienen el mismo volumen V A C D A’ D’ C’ h B P Q R S O P’ Q’ R’ S’ B h

21. Volumen de una pirámide triangular “ El volumen de una pirámide triangular es un tercio del producto del área de su base y su altura” Hipótesis: S-DEF pirámide triangular B área de la base h altura V volumen Tesis: V = ⅓ B . h A C S D E F N P M

22. Demostración: ASCDEF prisma triangular de base DEF y de altura H Prisma ASCDEF = S-DEF + S-ADF + S-AFC ∆ ADF = ∆AFC y ∆DSE = ∆DSA Pirámides S-ADF y S-AFC tienen el mismo volumen Pirámides F-DSE y F-DSA tienen el mismo volumen Pirámides S-DEF , S-ADF y S-AFC tienen el mismo volumen V V p = 3V V p = B . h 3V = B . h V = ⅓ B . h

23. “ El volumen de una pirámide cualquiera es igual a un tercio del producto del área de la base por la medida de la altura” HIPOTESIS: ABCDEF es una pirámide cualquiera. B es la base de la pirámide. h es la altura y V es el volumen TESIS:

24. DEMOSTRACIÓN : Δ BED y Δ BFE

25. “ Dos tetraedros de igual altura y bases equivalentes, son equivalentes” HIPOTESIS: ABCD y A´B´C´D´ Son dos tetraedros de igual altura y bases equivalentes, es decir Área Δ BCD=Área Δ B´C`D` TESIS: Tetraedro ABCD es equivalente al tetraedro`B`C`D`.

26. Demostración: Llamamos V 1, V 2 y V 3 a los volúmenes de los prismas inscritos en el tetaedro ABCD y V´ 1, V´ 2 y V´ 3 a los volúmenes de los prismas inscritos en el tetaedro A´B´C´D´ V 1 =V´ 1 V 2 =V´ 2 V 3 =V´ 3 Sumando miembro a miembro: V 1 +V 2 + V 3 = V´ 1 +V´ 2 +V´ 3 V 1 +V 2 + V 3 +V 4 + … = V´ 1 +V´ 2 +V´ 3 +V´ 4 +….

27. (V 1 +V 2 + V 3 +V 4 + …)= V (volumen del tetaedro ABCD) (V´ 1 +V´ 2 +V´ 3 +V´ 4 +….) = V´ (volumen del tetraedro A´B´C´D´) V = V´ por lo tanto: Los tetraedros ABCD y A´B´C´D´

29. EJERCICIOS DE APLICACIÓN La base de una pirámide regular es un hexágono que tiene de perímetro 6.12m. La apotema de una de las caras laterales del triángulo mide los 2/3 del perímetro de la base y su altura es de 4m. Calcular: * Apotema de la base * Área total * Volumen

30. Datos: P= 6.12m Ap. lat.= (2/3m* 6.12m)= 4.08 m Altura de la Pira= 4m Ap. Base= ? Área Total= ? Volumen= ? Ap. lat.= c h= b ap.=a

32. V=1/3 B.h

34. “ Todo tronco de pirámide triangular de bases paralelas es equivalente a la suma de tres pirámides de la misma altura del tronco y cuyas bases son las dos del tronco y una media proporcional entre ambas” HIPOTESIS: ABCA´B´C´ es un tronco de pirámide triangular de bases paralelas de áreas B Y b TESIS: ABCA´B´C´ es equivalente a la suma de tres pirámides de altura igual a la del tronco y cuyas bases sean B, b y

35. DEMOSTRACIÓN : DM || BC Δ ABC ≈ Δ ADM

36. “ Un tronco de pirámide de bases paralelas es equivalente a un tronco de pirámide triangular de la misma altura y bases equivalentes a las del tronco dado” HIPOTESIS: ABCDEA´B´C´D´E´ es un tronco de pirámide cualquiera de bases paralelas TESIS: El volumen de ABCDEA´B´C´D´E´ = al volumen de MNPQRT MNPQRT es un tronco de pirámide triangular de la misma altura que el tronco dado y bases equivalentes a las del tronco dado y situadas en los planos α y β paralelos.

37. DEMOSTRACIÓN : S-ABCDE ≈ S`-MNP :. Volumen S-ABCDE = Volumen S`-MNP (1) A`B`C`D`E` ≈ QRT :. Volumen S-A`B`C`D`E` = Volumen S`-QRT (2) Vol SABCDE - Vol SA`B`C`D`E` = Vol S`MNP - Vol S`QRT (3) Vol SABCDE - Vol SA`B`C`D`E` = Vol ABCDEA´B´C´D´E´ (4) Vol S`MNP - Vol S`QRT = Vol. MNPQRT (5) :. Vol. de ABCDEA´B´C´D´E´ = al Vol. de MNPQRT